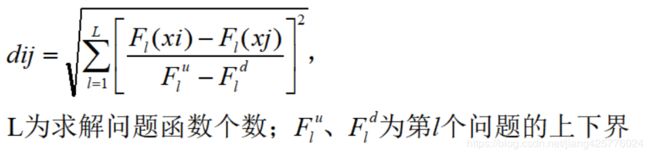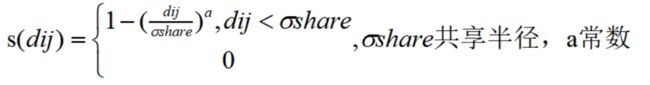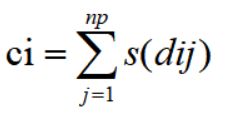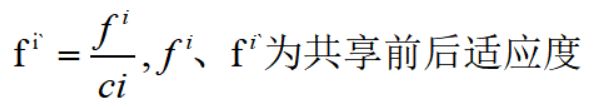NSGA-多目标遗传算法
NSGA-I
1.非支配个体排序:
- i=1;
- for all j=1,2..,n ; j!=i:
比较xi与xj的支配关系,并标记;
- if no any xj支配xi:
则标记xi为非被支配个体;
- i=i+1;
- go to (2) ,unitl all 非支配个体被判断标记出来;
- then get first F1={xi,xj,xk,...第一层非被支配个体}
- ignore 被标记为非支配的x;
do (1)-(6) until all 个体被标记为非支配体
- 为每一层F1,F2,...指定一个虚拟适应度,F1:1,F2:0.9,F3:0.8,...
2.共享适应度计算:
p层Fp上有np个个体,虚拟适应值为fp;i,j=1,2,...np;
(2)
(3)loop j=1,2,...np.计算:
(4)xi的共享适应度计算:
(5)loop (1)-(4),until all 个体的共享适应度计算完成;
NSGA-II
快速排序,拥挤度策略,精英策略
每个个体属性:ni(种群中能支配xi的个体的数量)、Si(被xi支配的个体的集合)
1.计算支配层级:
fast-nodominate-sort(P)
P={x1,x2,x...,xm}
(1)计算所有个体的ni,Si;
(2) found all xi where xi.ni==0
input xi into F1 where xi.ni==0
(3) for xj{nj,Sj} in F1:
for xk in xj.Sj:
xk.nk--;
if xk.nk==0:
H.putinto(xk)
(4)此时,F1为一级非支配层个体集;设F1层里面的个体一个相同的序列:irank=当前层+1
(5)用H作为新的集合F2,fast-nodominate-sort(F2)
loop (2)-(4) until all x1,2,...m被分层完到F1,F2,....2.拥挤度计算
原一版中,采用共享函数以确保种群多样性,需要指定共享半径σshare;II代提出了拥挤度概念,表示个体周围的密度,id;意义是个体xi周围只包含xi不包含其它个体的最大长方形区域。
拥挤度计算函数:
crowding-distance(L)
l=|L| 个体数;
L[i].id=0 每个个体初始拥挤度为0 ;
for fi in objectfuncs F={f1,f2,...,fm} : 遍历所有目标函数
L=sort(L,fi) 在fi目标函数下对L中个体进行非支配排序
L[1].id=L[l].id=∞ 第一个和最后一个不可能有上下界,无限大
for i=2至(l-1):
L[i].id=L[i].id+(fi(L[i+1])-fi(L[i-1]))/(max(fi)-min(fi))最后:
id小的个体周围比较拥挤;为了维持种群多样性,需要一个拥挤度比较算子以确保能收敛到均匀的pareto面;
经过1获得的排序irank,和2获得的拥挤度id,可定义偏序关系(比较解的好坏的时候):
如果两个体支配排序不同,先取小的;如果同支配级,取不拥挤的即拥挤度id大的。算法:
t=0
随机产生Pt={x1,x2,...,xN}
对所有个体计算快速支配排序:fast-nodominate-sort(Pt);
选择、交叉、变异产生下一代:Qt=GA(Pt);
然后执行算法:
NSGA-II(Pt,Qt)
Rt = Pt+Qt 第t代的父代Pt,第t代的新种群Qt合并,2N个体
F = fast-nodominate-sort(Rt) 父子代参与快速非支配排序,F={F1,F2,...}
Pt+1 = ∅ 下一代初始空
i = 0
while |Pt+1|+|Fi|<=N: //i=1,2,....没有被填满
crowding-distance(Fi) 计算Fi层中个体拥挤度
P(t+1) = P(t+1)∪Fi Fi层中个体并入下一代
i = i+1
sort(Fi,NSGAII实现
我自己Github实现:
https://github.com/425776024/NSGA-II
2019-11-18 更新
发现有这么一个库很不错,已经集成了这么多算法,本人写的真的有误人子弟,献丑了,想了解更好的实现细节的也可以参考这个库的源码
Single-objective: Genetic Algorithm, Differential Evolution, Nelder Mead
Multi-objective: NSGA-II, R-NSGA-II, NSGA-III, R-NSGA-III, U-NSGA-III, MOEA/D
网址:https://pymoo.org/