kaggle入门级项目（Titanic）

前言

从事数据科学方面工作的人应该都听说过kaggle比赛，当然对于机器学习方面感兴趣的学生小伙伴来说，kaggle也是一个可以实战的地方，从机器学习理论转向实战其实是个不小的挑战，但在应用时不需要每行代码都去自己敲打，python具有相对成熟的包和库，调用相应的函数设置参数即可实现相应的机器学习算法，同时matplotlib和seaborn库能够可视化数据，这些对于数据分析和建模都十分有用，该篇博客针对入门级项目泰坦尼克号进行了详细的介绍，本博客针对有一定的机器学习理论基础的人，但在实战上缺乏经验。个人认为进行机器学习实战时前期需要大致了解某个库的作用，但其具体的使用不用详细去斟酌，首先寻找个例程，跟随例程去实现，在实现中查阅相关资料是学的最快的一种方式。入门级的kaggle项目有三个，分别为titanic（分类），房价预测（回归）和手写体识别（计算机视觉），在熟悉该三个项目的基础上再进行其它比赛是个不错的选择。

初识Titanic数据

简单来说Titanic项目是个二分分类项目，即结果只有两种情况，存活为1，死亡为0，数据集中会给出每位乘客的多条信息，和是否存活，自己要做的工作是给出一个人的信息判断其是否能存活。在kaggle上下载数据集，解压。首先对数据集要有个大致的了解，这里采用pandas库进行。本文代码是在jupyter notebook中实现的。
首先导入需要用到的库

from sklearn import svm, tree, linear_model, neighbors, naive_bayes, ensemble, discriminant_analysis, gaussian_process
from xgboost import XGBClassifier

from sklearn.preprocessing import OneHotEncoder, LabelEncoder
from sklearn import feature_selection
from sklearn import model_selection
from sklearn import metrics

import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.pylab as pylab
import seaborn as sns
from pandas.tools.plotting import scatter_matrix

import pandas as pd
%matplotlib inline          #显示图像
mpl.style.use("ggplot")     #将matplotlib设置为ggplot格式
sns.set_style("white")      #将seaborn图形的背景设为白色
pylab.rcParams['figure.figsize'] = 12,8

接下来使用pandas库对数据进行大致的分析了解

train_data=pd.read_csv("train.csv")       #训练数据
test_data=pd.read_csv("test.csv")			#测试数据
data1=train_data.copy(deep=True)     #深拷贝，改变复制值原值不变。对训练数据进行拷贝，接下来的各种特征操作将在该副本中进行。
data_cleaner=[data1,test_data]             #将训练数据和测试数据进行联合，形成总数居集。
train_data.info()                                     #大致了解训练数据的基本信息
train_data.sample(10)                            #对训练数据进行随机采样来观察数据的组成

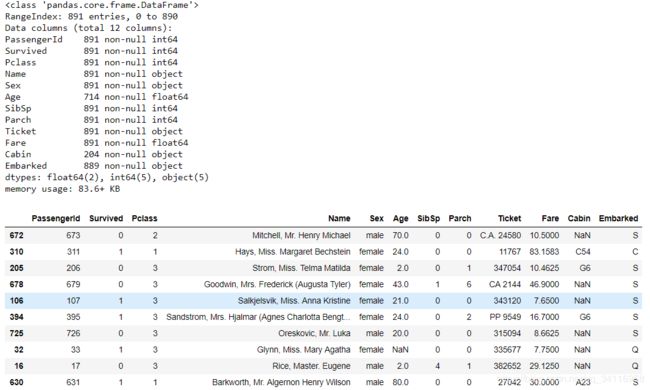
从训练数据的总体信息可知每个乘客有12个属性，分别为乘客ID，乘客等级，乘客姓名，性别，年龄，堂兄弟/妹个数，父母与小孩个数，船票信息，票价，客舱，登船港口，其中年龄和客舱部分缺失。

• 生存值是需要预测的值，必须注意到，更多的特征值不一定会使模型的效果变好，正确的特征值才会使模型变好。
• 假设乘客ID和船票信息是随机的唯一标识符，其对输出结果没有影响，因此将其除去。
• Pclass变量是票等级的有序数据类型，是社会经济地位(SES)的代理，表示1 =上层阶级、2 =中产阶级和3 =下层阶级。
• Name变量是一种标称数据类型。它可以用于特征工程中，从头衔中提取性别，从姓氏中提取家庭规模，从博士或硕士等头衔中提取社会经济地位。由于这些变量已经存在，我们将使用它来查看title是否与master一样起作用。
• 性别和登船港口是一种标称数据类型。它们将被转换为虚拟变量进行数学计算。
• 年龄和票价变量是连续的定量数据类型。
• SibSp代表在船上的相关兄弟姐妹/配偶的数量，Parch代表在船上的相关父母/孩子的数量。两者都是离散的定量数据类型。这可以用于特性工程来创建一个家庭大小，并且是单独可变的。
• 客舱变量是一种标称数据类型，可用于特征工程中描述事故发生时船上的大致位置和甲板位置。但是，由于有许多空值，所以它不增加值，因此被排除在分析之外。

数据清洗：纠正，填补，创造和转化

纠正： 检查数据是否存在不合理的值，若存在则需要对其进行修正，如年龄是800而不是80，
填补： 在age，cabin和embarked属性中含有缺失值和null，因此需要填补这些缺失值，定性数据的一种基本方法是使用模式输入。定量数据的基本方法是使用均值、中值或均值+随机标准差进行估算。对于该数据集年龄采用平均值进行计算，删除cabin属性，embark使用模式进行输入。后续的模型迭代可能会修改这个决策，以确定它是否提高了模型的准确性。
创造： 特征工程指的是我们利用已有的属性来创造新的属性，该新的属性能够为我们的输出提供新的信号。在该数据集中我们会创造一个新的title属性来在生存预测中产生作用。
转化： 我们将处理格式化。没有日期或货币格式，只有数据类型格式。我们将分类数据作为对象导入，这使得数学计算变得困难。对于这个数据集，我们将把对象数据类型转换为分类虚拟变量。

print('Train columns with null values:\n', data1.isnull().sum())      #计算训练集中缺失值的总数
print("-"*10)

print('Test/Validation columns with null values:\n', test_data.isnull().sum())
print("-"*10)

train_data.describe(include = 'all')                 #对训练数据进行总体描述

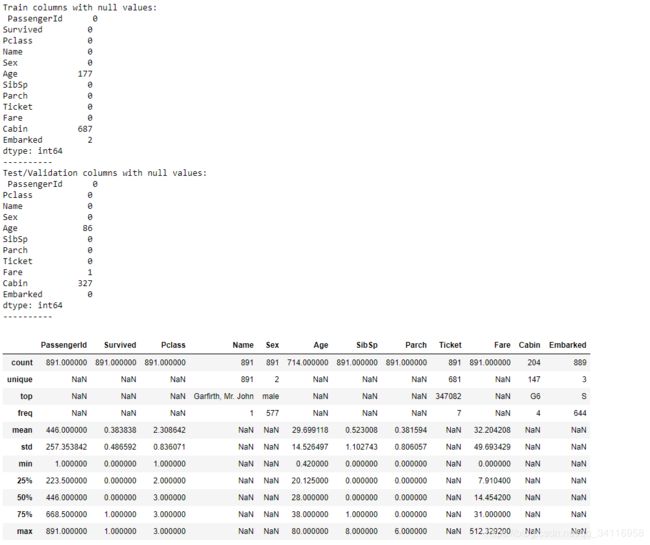
由结果可知Age缺失177个，Cabin缺失687个，Embarked缺失2个。
填补数据

for dataset in data_cleaner:
    dataset["Age"].fillna(dataset["Age"].median(),inplace=True)            #使用Age的中位数填充，inplace=True为
    #直接在原数据上修改，不生成新的副本
    dataset["Embarked"].fillna(dataset["Embarked"].mode()[0],inplace=True)    #使用Embarked中出现频率最高的填充 
    dataset["Fare"].fillna(dataset["Fare"].median(),inplace=True)
    
drop_column = ['PassengerId','Cabin', 'Ticket']              #将要除去ID，Cabin和Ticket三种属性
data1.drop(drop_column,axis=1,inplace=True)             #在原数据上删除该三个属性，不生成副本
data1.describe(include="all")

创造数据（特征工程）

for dataset in data_cleaner:
    dataset["FamilySize"]=dataset["SibSp"]+dataset["Parch"]+1      #增加总家庭人数作为新生成的特征
    dataset["IsAlone"]=1                                           #增加是否为单人属性，若为单人则设为1，否则为0
    dataset["IsAlone"].loc[dataset["FamilySize"]>1]=0
    dataset["Title"]=dataset["Name"].str.split(",",expand=True)[1].str.split(".",expand=True)[0]  #新增title属性
    dataset["FareBin"]=pd.qcut(dataset["Fare"],4)       #将Fare分为4个组，每个bin中的数据长度相同
    dataset["AgeBin"]=pd.cut(dataset["Age"].astype(int),5)   #将年龄分为5个bins，每个bin的长度相同

stat_min=10
title_names=(data1["Title"].value_counts()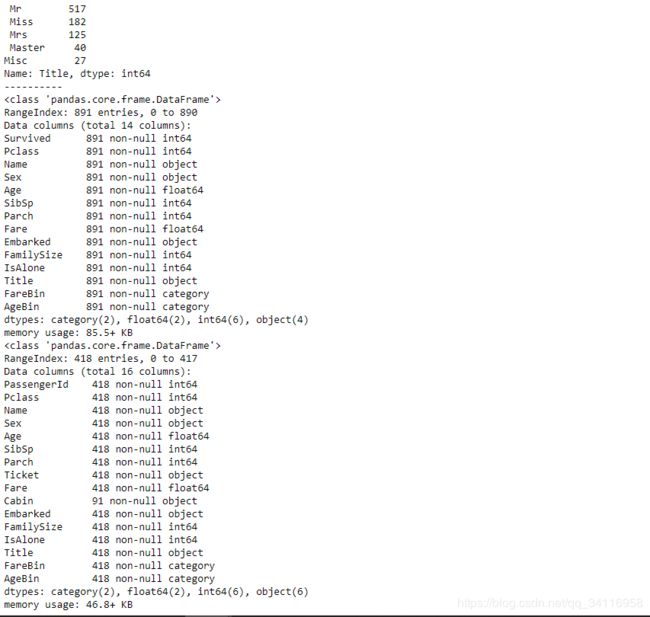

转化
我们将把分类数据转换为虚拟变量进行数学分析。编码分类变量有多种方法;我们将使用sklearn和panda函数。

label=LabelEncoder()
for dataset in data_cleaner:
    dataset["Sex_Code"]=label.fit_transform(dataset["Sex"])      #对数据进行编码，将字符串类型的属性转化为整形
    dataset["Embarked_Code"]=label.fit_transform(dataset["Embarked"])
    dataset["Title_Code"]=label.fit_transform(dataset["Title"])
    dataset["AgeBin_Code"]=label.fit_transform(dataset["AgeBin"])
    dataset["FareBin_Code"]=label.fit_transform(dataset["FareBin"])
Target=["Survived"]
#每位乘客的特征属性
data1_x = ['Sex','Pclass', 'Embarked', 'Title','SibSp', 'Parch', 'Age', 'Fare', 'FamilySize', 'IsAlone'] #单纯的名字/值属性
data1_x_calc = ['Sex_Code','Pclass', 'Embarked_Code', 'Title_Code','SibSp', 'Parch', 'Age', 'Fare'] #编码后易于数学计算的属性
data1_xy =  Target + data1_x
print('Original X Y: ', data1_xy, '\n')
data1_x_bin = ['Sex_Code','Pclass', 'Embarked_Code', 'Title_Code', 'FamilySize', 'AgeBin_Code', 'FareBin_Code']#移除连续变量后的属性
data1_xy_bin = Target + data1_x_bin
print('Bin X Y: ', data1_xy_bin, '\n')
data1_dummy = pd.get_dummies(data1[data1_x])    #进行one-hot编码，得到变量的虚拟变量
# print(data1_dummy)
data1_x_dummy = data1_dummy.columns.tolist()    #虚拟变量变成列表形式
# data1_x_dummy
data1_xy_dummy = Target + data1_x_dummy
print('Dummy X Y: ', data1_xy_dummy, '\n')
data1_dummy.head()

目前为止，对特征的大致处理已经完成接下来对数据进行分割和可视化特征对结果的影响。
数据分割
因为测试集是最终将要提交和预测的数据集，因此在训练不能涉及到该测试集，为了防止过拟合，将训练集分为训练集和验证集。

train1_x, test1_x, train1_y, test1_y = model_selection.train_test_split(data1[data1_x_calc], data1[Target], random_state = 0)          #默认为3：1分割
train1_x_bin, test1_x_bin, train1_y_bin, test1_y_bin = model_selection.train_test_split(data1[data1_x_bin], data1[Target] , random_state = 0)
train1_x_dummy, test1_x_dummy, train1_y_dummy, test1_y_dummy = model_selection.train_test_split(data1_dummy[data1_x_dummy], data1[Target], random_state = 0)

用统计数据进行探索性分析

现在数据已被清理，我们将使用描述性统计和图形化统计来研究数据，以描述和总结变量。在这个阶段，将会发现自己对特性进行分类，并确定它们与目标变量以及彼此之间的相关性。
分析离散型变量与目标值之间的相关性

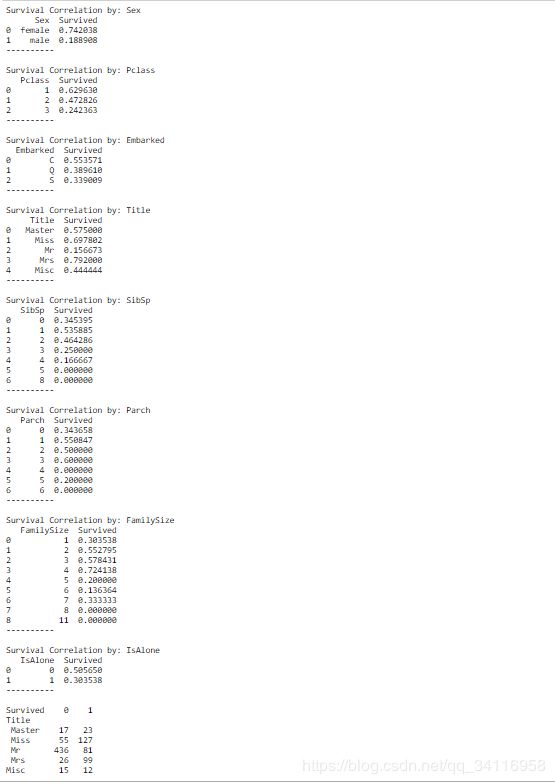
for x in data1_x:
    if data1[x].dtype!='float64':      #数据类型为float64的是连续型变量，反之为离散型变量
        print("Survival Correlation by:", x)
        print(data1[[x,Target[0]]].groupby(x,as_index=False).mean())  #按照x的取值对数据进行分组处理，并计算均值
        print("-"*10,"\n")
print(pd.crosstab(data1["Title"],data1[Target[0]]))        #以Title和Target分别为行和列计算频数。按Title分组，统计各个组中的生存人数

出于学习的目的，绘制不同类型的图表。

#设置图表的大小
plt.figure(figsize=[16,12])
#绘制箱型图
plt.subplot(231)
plt.boxplot(x=data1["Fare"],showmeans = True,meanline=True)#meanline：是否用线的形式表示均值，默认用点来表示；
                                                           #showmeans：是否显示均值，默认不显示；
plt.title("Fare Boxplot")
plt.ylabel("Fare($)")

plt.subplot(232)
plt.boxplot(data1['Age'], showmeans = True, meanline = True)
plt.title('Age Boxplot')
plt.ylabel('Age (Years)')

plt.subplot(233)
plt.boxplot(data1['FamilySize'], showmeans = True, meanline = True)
plt.title('Family Size Boxplot')
plt.ylabel('Family Size (#)')

#绘制直方图
plt.subplot(234)
plt.hist(x = [data1[data1['Survived']==1]['Fare'], data1[data1['Survived']==0]['Fare']], 
         stacked=True, color = ['g','r'],label = ['Survived','Dead'])      			#stack是否为堆叠放
plt.title('Fare Histogram by Survival')
plt.xlabel('Fare ($)')
plt.ylabel('# of Passengers')
plt.legend()

plt.subplot(235)
plt.hist(x = [data1[data1['Survived']==1]['Age'], data1[data1['Survived']==0]['Age']], 
         stacked=True, color = ['g','r'],label = ['Survived','Dead'])
plt.title('Age Histogram by Survival')
plt.xlabel('Age (Years)')
plt.ylabel('# of Passengers')
plt.legend()

plt.subplot(236)
plt.hist(x = [data1[data1['Survived']==1]['FamilySize'], data1[data1['Survived']==0]['FamilySize']], 
         stacked=True, color = ['g','r'],label = ['Survived','Dead'])
plt.title('Family Size Histogram by Survival')
plt.xlabel('Family Size (#)')
plt.ylabel('# of Passengers')
plt.legend()

箱型图反映了单一变量的分布，这里显示了Fare、Age和FamilySize的分布特性，包括中位数、平均值、前1/4、后1/4、异常值等信息。直方图反映了Fare、Age和FamilySize的数量分布特性。
接下来尝试使用seaborn库进行条形图和点状图的绘制。

fig,saxis=plt.subplots(2,3,figsize=(16,12))

sns.barplot(x = 'Embarked', y = 'Survived', data=data1, ax = saxis[0,0])
sns.barplot(x = 'Pclass', y = 'Survived', order=[1,2,3], data=data1, ax = saxis[0,1])
sns.barplot(x = 'IsAlone', y = 'Survived', order=[1,0], data=data1, ax = saxis[0,2])

sns.pointplot(x = 'FareBin', y = 'Survived',  data=data1, ax = saxis[1,0])
sns.pointplot(x = 'AgeBin', y = 'Survived',  data=data1, ax = saxis[1,1])
sns.pointplot(x = 'FamilySize', y = 'Survived', data=data1, ax = saxis[1,2])

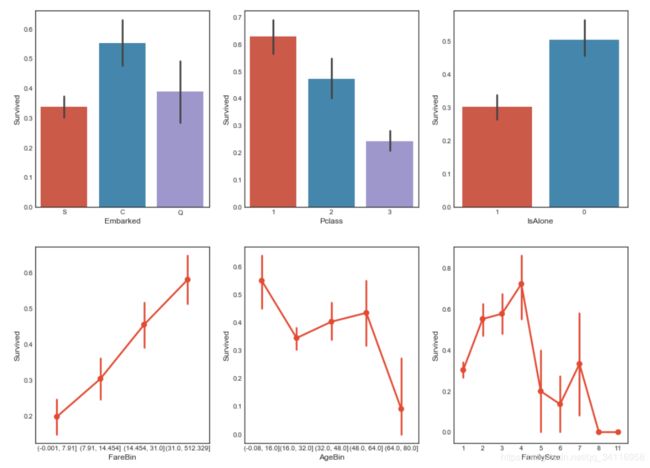
条形图表示数值变量与每个矩形高度的中心趋势的估计值，并使用误差线提供关于该估计值附近的不确定性的一些指示。关于结果的解释：Seaborn会对"Embarked"，“Pclass”,"isAlone"列中的数值进行归类后按照estimator参数的方法（默认为平均值）计算相应的值，计算出来的值就作为条形图所显示的值,黑线默认情况标识了95%的置信区间。何为95%的置信区间？95%的置信区间指的是对于当前样本所属的分布而言，当有个新的值产生时，这个值有95%的可能性在该区间内，5%的可能性不在该区间内。barplot主要用来描述样本的均值和置信区间。 pointplot和barplot意义是一样的，也是来描述样本的均值和置信区间。
接下来对定性数据Pclass进行分析。 我们知道Pclass在生存中是十分重要的，因此在Pclass的基础上对该属性进行分析。

fig, (axis1,axis2,axis3) = plt.subplots(1,3,figsize=(14,12))

sns.boxplot(x = 'Pclass', y = 'Fare', hue = 'Survived', data = data1, ax = axis1)   #x,y:dataframe中的列名或矢量数据，
#data:dataframe或者数组  hue:dataframe的列名，按照列名中的分类形成的分类条形图
axis1.set_title('Pclass vs Fare Survival Comparison')

sns.violinplot(x = 'Pclass', y = 'Age', hue = 'Survived', data = data1, split = True, ax = axis2)
axis2.set_title('Pclass vs Age Survival Comparison')     #violinplot在boxplot的基础上可以绘出各个区间的密度分布情况

sns.boxplot(x = 'Pclass', y ='FamilySize', hue = 'Survived', data = data1, ax = axis3)
axis3.set_title('Pclass vs Family Size Survival Comparison')

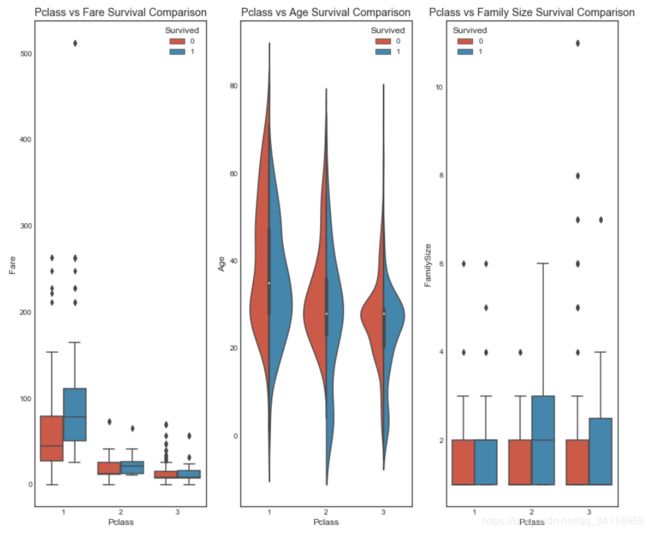
由小提琴图可看出不同的Pclass中Age的密度分布情况。
接下来对定性数据Sex进行分析。 在Sex作为第一特征基础上增加其它特征进行分析。

fig, qaxis = plt.subplots(1,3,figsize=(14,12))

sns.barplot(x = 'Sex', y = 'Survived', hue = 'Embarked', data=data1, ax = qaxis[0])
axis1.set_title('Sex vs Embarked Survival Comparison')

sns.barplot(x = 'Sex', y = 'Survived', hue = 'Pclass', data=data1, ax  = qaxis[1])
axis1.set_title('Sex vs Pclass Survival Comparison')

sns.barplot(x = 'Sex', y = 'Survived', hue = 'IsAlone', data=data1, ax  = qaxis[2])
axis1.set_title('Sex vs IsAlone Survival Comparison')

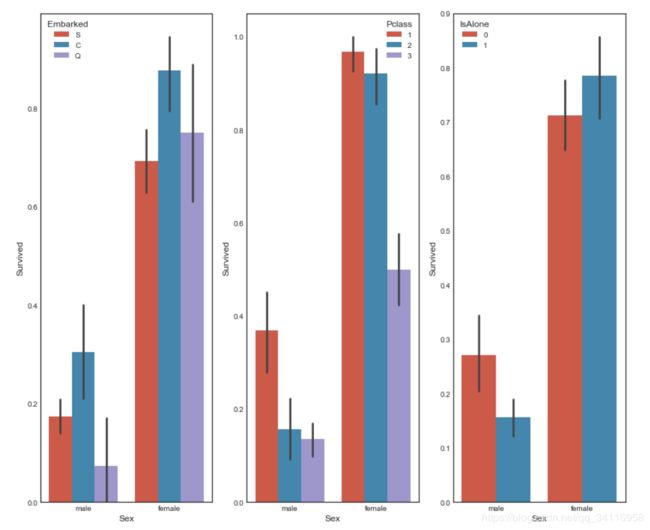
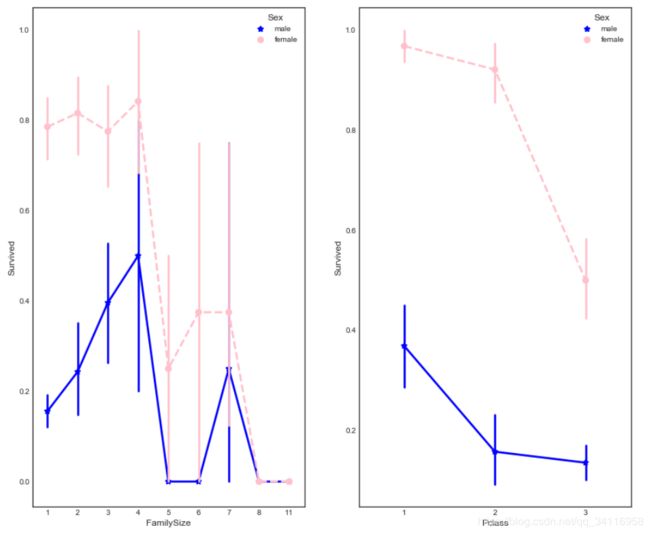
进一步比较，FamilySize和Pclass分别与Sex联合对生存的影响。

fig, (maxis1, maxis2) = plt.subplots(1, 2,figsize=(14,12))

#how does family size factor with sex & survival compare
sns.pointplot(x="FamilySize", y="Survived", hue="Sex", data=data1,
              palette={"male": "blue", "female": "pink"},
              markers=["*", "o"], linestyles=["-", "--"], ax = maxis1)

#how does class factor with sex & survival compare
sns.pointplot(x="Pclass", y="Survived", hue="Sex", data=data1,
              palette={"male": "blue", "female": "pink"},
              markers=["*", "o"], linestyles=["-", "--"], ax = maxis2)

Embarked和Pclass和Sex对生存的影响。

#FacetGrid是一个绘制多个表格的接口
#步骤：
#1、实例化对象
#2、map，映射到具体的 seaborn 图表类型
#3、添加图例
#col=“Embarked表示是从列的方向上看，是Embarked字段
e = sns.FacetGrid(data1, col = 'Embarked')
e.map(sns.pointplot, 'Pclass', 'Survived', 'Sex', ci=95.0, palette = 'deep')
e.add_legend()

对年龄分布的生存情况进行绘制

a = sns.FacetGrid( data1, hue = 'Survived', aspect=4 )
a.map(sns.kdeplot, 'Age', shade= True )
a.set(xlim=(0 , data1['Age'].max()))
a.add_legend()

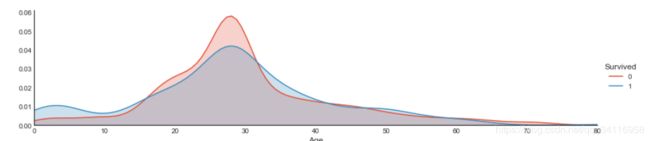
由上图可看出不同年龄段中生存的分布。
对性别和Pclass的生存进行分析

h = sns.FacetGrid(data1, row = 'Sex', col = 'Pclass', hue = 'Survived')
h.map(plt.hist, 'Age', alpha = .75)
h.add_legend()

有结果可知，男性Pclass为3和2的几乎没有存活的，女性Pclass为1和2的几乎全部存活。
对全部数据的相关性进行分析，这里绘制heatmap。

def correlation_heatmap(df):
    _ , ax = plt.subplots(figsize =(14, 12))
    colormap = sns.diverging_palette(220, 10, as_cmap = True)
    
    _ = sns.heatmap(
        df.corr(), 
        cmap = colormap,
        square=True, 
        cbar_kws={'shrink':.9 }, 
        ax=ax,
        annot=True, 
        linewidths=0.1,vmax=1.0, linecolor='white',
        annot_kws={'fontsize':12 }
    )
    
    plt.title('Pearson Correlation of Features', y=1.05, size=15)

correlation_heatmap(data1)

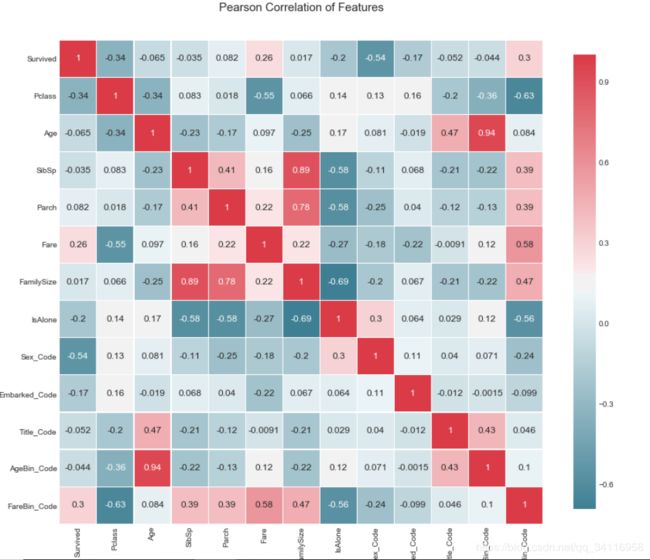
由热图可分析出各个特征值与目标生存值间的相关性。绝对值越接近1说明相关性越强。

模型的构造

目前存在许多的机器学习方法，然而可分为四类：分类、回归、聚类和降维。这里针对分类和回归问题，这里广泛的理解，目标变量是连续性的为回归问题，目标变量是离散的为分类问题。另一方面逻辑回归问题虽然名字里有回归但是其实际上是分类问题，目标值为两个。因为我们的问题是生存和死亡，因此为分类问题。
对于初学者来说，经常会问那种模型最好，这里需要声明的是没有超级完美的模型能够适应任何问题。最好的方法就是尝试多种模型，对其进行微调比较性能好坏。对于初学者来说，首先从Trees, Bagging, Random Forests, and Boosting开始是比较好的。它们基本上是决策树的不同实现，这是最容易学习和理解的概念。下面将讨论它们，它们比SVC之类的东西更容易调优。下面，我将概述如何运行和比较几个MLAs，但是这个内核的其余部分将集中于通过决策树及其衍生物学习数据建模。

MLA=[
    #Ensemble Methods 集成方法
    ensemble.AdaBoostClassifier(),
    ensemble.BaggingClassifier(),
    ensemble.ExtraTreesClassifier(),
    ensemble.GradientBoostingClassifier(),
    ensemble.RandomForestClassifier(),
    
    #Gaussian Process  高斯过程
    gaussian_process.GaussianProcessClassifier(),
    
    #GLM   广义线性模型
    linear_model.LogisticRegressionCV(),
    linear_model.PassiveAggressiveClassifier(),
    linear_model.RidgeClassifierCV(),
    linear_model.SGDClassifier(),
    linear_model.Perceptron(),
    
    #Navies Bayes  朴素贝叶斯
    naive_bayes.BernoulliNB(),
    naive_bayes.GaussianNB(),
    
    #Nearest Neighbor  #最近邻法
    neighbors.KNeighborsClassifier(),
    
    #SVM
    svm.SVC(probability=True),
    svm.NuSVC(probability=True),
    svm.LinearSVC(),
    
    #Trees    
    tree.DecisionTreeClassifier(),
    tree.ExtraTreeClassifier(),
    
    #Discriminant Analysis   判别分析
    discriminant_analysis.LinearDiscriminantAnalysis(),
    discriminant_analysis.QuadraticDiscriminantAnalysis(),

    
    #xgboost: 
    XGBClassifier()
]

#30%作为验证集，60%作为训练集，10%预留
cv_split = model_selection.ShuffleSplit(n_splits = 10, test_size = .3, train_size = .6, random_state = 0 )
#n_splits:int, 划分训练集、测试集的次数，默认为10
#test_size:float, int, None, default=0.1； 测试集比例或样本数量，该值为[0.0, 1.0]内的浮点数时，表示测试集占总样本的比例；该值为整型值时，表示具体的测试集样本数量；train_size不设定具体数值时，该值取默认值0.1，train_size设定具体数值时，test_size取剩余部分
#train_size:float, int, None； 训练集比例或样本数量，该值为[0.0, 1.0]内的浮点数时，表示训练集占总样本的比例；该值为整型值时，表示具体的训练集样本数量；该值为None(默认值)时，训练集取总体样本除去测试集的部分
#random_state:int, RandomState instance or None；随机种子值，默认为None
#新建一个表来比较算法的性能
MLA_columns = ['MLA Name', 'MLA Parameters','MLA Train Accuracy Mean', 'MLA Test Accuracy Mean', 'MLA Test Accuracy 3*STD' ,'MLA Time']
MLA_compare = pd.DataFrame(columns = MLA_columns)
MLA_predict = data1[Target]
row_index=0
for alg in MLA:
    #设置名字和参数
    MLA_name=alg.__class__.__name__
    MLA_compare.loc[row_index,"MLA Name"]=MLA_name
    MLA_compare.loc[row_index,"MLA Parameters"]=str(alg.get_params())
    #使用交叉验证的模型分数
    cv_results=model_selection.cross_validate(alg,data1[data1_x_bin],data1[Target],cv=cv_split)
    MLA_compare.loc[row_index,"MLA_Time"]=cv_results["fit_time"].mean()
    MLA_compare.loc[row_index, 'MLA Train Accuracy Mean'] = cv_results['train_score'].mean()
    MLA_compare.loc[row_index, 'MLA Test Accuracy Mean'] = cv_results['test_score'].mean()   
    MLA_compare.loc[row_index, 'MLA Test Accuracy 3*STD'] = cv_results['test_score'].std()*3
    #在测试集上进行测试
    alg.fit(data1[data1_x_bin], data1[Target])
    MLA_predict[MLA_name] = alg.predict(data1[data1_x_bin])
    row_index+=1
#
MLA_compare.sort_values(by = ['MLA Test Accuracy Mean'], ascending = False, inplace = True)
MLA_compare

对不同的算法模型的准确率进行比较，绘制出下面的柱状图。

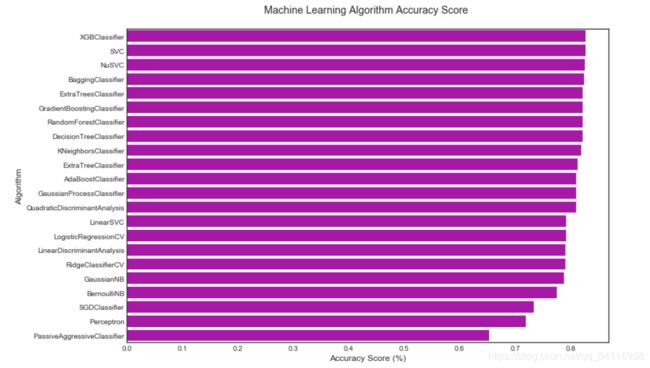
由结果图可看出XGBClassifier分类器的准确率最高，前几种的准确率差不多。
对模型的性能进行评价
经过数据清洗，分析和机器学习算法后我们可以得到82%的预测准确率，看起来还不错，但是我们如何知道该算法性能的好坏呢，这时我们需要得到一个基准准确率。这是一个逻辑回归问题，只有生存和死亡两种情况，因此最简单的也有50%的准确率，如果我们知道一些基本信息，如2224人中1502人死亡，即死亡率为67.5%，那么得到一个算法，即预测值全部为死亡，则算法准确率为67.5%，因此将68%作为最坏的模型性能。利用频率信息可以构建自己的决策树，在该假设下，决策树的准确率为82%。将82%作为基准性能，比该性能差的模型是无意义的。
使用交叉验证对模型性能优化
首先使用一个基准模型，这里采用决策树模型，其中超参数采用默认值，之后再对其进行微调，从而观察超参数对模型的影响。
决策树模型及其参数：

class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)

#采用默认参数的决策树模型
dtree=tree.DecisionTreeClassifier(random_state=0)
base_results=model_selection.cross_validate(dtree,data1[data1_x_bin],data1[Target],cv=cv_split,return_train_score=True)           #交叉验证
dtree.fit(data1[data1_x_bin], data1[Target])

print('BEFORE DT Parameters: ', dtree.get_params())
print("BEFORE DT Training w/bin score mean: {:.2f}". format(base_results['train_score'].mean()*100)) 
print("BEFORE DT Test w/bin score mean: {:.2f}". format(base_results['test_score'].mean()*100))
print("BEFORE DT Test w/bin score 3*std: +/- {:.2f}". format(base_results['test_score'].std()*100*3))
#print("BEFORE DT Test w/bin set score min: {:.2f}". format(base_results['test_score'].min()*100))
print('-'*10)
#对超参数进行微调
param_grid = {'criterion': ['gini', 'entropy'],  #特征选择标准，采用熵值或gini系数
              #'splitter': ['best', 'random'], #特征划分标准; 前者在特征的所有划分点中找出最优的划分点。后者是随机的在部分划分点中找局部最优的划分点。 默认的”best”适合样本量不大的时候，而如果样本数据量非常大，此时决策树构建推荐”random” 。
              'max_depth': [2,4,6,8,10,None], #决策树最大深度一般来说，数据少或者特征少的时候可以不管这个值。如果模型样本量多，特征也多的情况下，推荐限制这个最大深度，具体的取值取决于数据的分布。常用的可以取值10-100之间。常用来解决过拟合
              #'min_samples_split': [2,5,10,.03,.05], #内部节点再划分所需最小样本数
              #'min_samples_leaf': [1,5,10,.03,.05], #叶子节点最少样本数，如果是 int，则取传入值本身作为最小样本数； 如果是 float，则去 ceil(min_samples_leaf * 样本数量) 的值作为最小样本数，即向上取整。 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。
              #'max_features': [None, 'auto'], #max features to consider when performing split; default none or all
              'random_state': [0] #seed or control random number generator: https://www.quora.com/What-is-seed-in-random-number-generation
             }

#print(list(model_selection.ParameterGrid(param_grid)))

#choose best model with grid_search: #http://scikit-learn.org/stable/modules/grid_search.html#grid-search
#http://scikit-learn.org/stable/auto_examples/model_selection/plot_grid_search_digits.html
tune_model = model_selection.GridSearchCV(tree.DecisionTreeClassifier(), param_grid=param_grid, scoring = 'roc_auc', 
                                          cv = cv_split,return_train_score=True)    #采用网格搜索来确定最优参数
tune_model.fit(data1[data1_x_bin], data1[Target])

#print(tune_model.cv_results_.keys())
#print(tune_model.cv_results_['params'])
print('AFTER DT Parameters: ', tune_model.best_params_)
#print(tune_model.cv_results_['mean_train_score'])
print("AFTER DT Training w/bin score mean: {:.2f}". format(tune_model.cv_results_['mean_train_score'][tune_model.best_index_]*100)) 
#print(tune_model.cv_results_['mean_test_score'])
print("AFTER DT Test w/bin score mean: {:.2f}". format(tune_model.cv_results_['mean_test_score'][tune_model.best_index_]*100))
print("AFTER DT Test w/bin score 3*std: +/- {:.2f}". format(tune_model.cv_results_['std_test_score'][tune_model.best_index_]*100*3))
print('-'*10)

有结果可知，经过参数微调后模型性能有所提高。
特征选择
正如之前所说，更多的预测变量不会让模型的性能提高，但是正确的预测算子会提高算法性能，因此下一步是特征选择。

#基准模型
print('BEFORE DT RFE Training Shape Old: ', data1[data1_x_bin].shape) 
print('BEFORE DT RFE Training Columns Old: ', data1[data1_x_bin].columns.values)

print("BEFORE DT RFE Training w/bin score mean: {:.2f}". format(base_results['train_score'].mean()*100)) 
print("BEFORE DT RFE Test w/bin score mean: {:.2f}". format(base_results['test_score'].mean()*100))
print("BEFORE DT RFE Test w/bin score 3*std: +/- {:.2f}". format(base_results['test_score'].std()*100*3))
print('-'*10)
#特征选择
dtree_rfe=feature_selection.RFECV(dtree,step=1,scoring="accuracy",cv=cv_split)
dtree_rfe.fit(data1[data1_x_bin],data1[Target])
X_rfe = data1[data1_x_bin].columns.values[dtree_rfe.get_support()]
rfe_results = model_selection.cross_validate(dtree, data1[X_rfe], data1[Target], cv  = cv_split,return_train_score=True)
print('AFTER DT RFE Training Shape New: ', data1[X_rfe].shape) 
print('AFTER DT RFE Training Columns New: ', X_rfe)

print("AFTER DT RFE Training w/bin score mean: {:.2f}". format(rfe_results['train_score'].mean()*100)) 
print("AFTER DT RFE Test w/bin score mean: {:.2f}". format(rfe_results['test_score'].mean()*100))
print("AFTER DT RFE Test w/bin score 3*std: +/- {:.2f}". format(rfe_results['test_score'].std()*100*3))
print('-'*10)
#对特征选择后的模型进行微调
rfe_tune_model = model_selection.GridSearchCV(tree.DecisionTreeClassifier(), param_grid=param_grid, 
                                              scoring = 'roc_auc', cv = cv_split,return_train_score=True)
rfe_tune_model.fit(data1[X_rfe], data1[Target])

#print(rfe_tune_model.cv_results_.keys())
#print(rfe_tune_model.cv_results_['params'])
print('AFTER DT RFE Tuned Parameters: ', rfe_tune_model.best_params_)
#print(rfe_tune_model.cv_results_['mean_train_score'])
print("AFTER DT RFE Tuned Training w/bin score mean: {:.2f}". format(rfe_tune_model.cv_results_['mean_train_score'][tune_model.best_index_]*100)) 
#print(rfe_tune_model.cv_results_['mean_test_score'])
print("AFTER DT RFE Tuned Test w/bin score mean: {:.2f}". format(rfe_tune_model.cv_results_['mean_test_score'][tune_model.best_index_]*100))
print("AFTER DT RFE Tuned Test w/bin score 3*std: +/- {:.2f}". format(rfe_tune_model.cv_results_['std_test_score'][tune_model.best_index_]*100*3))
print('-'*10)

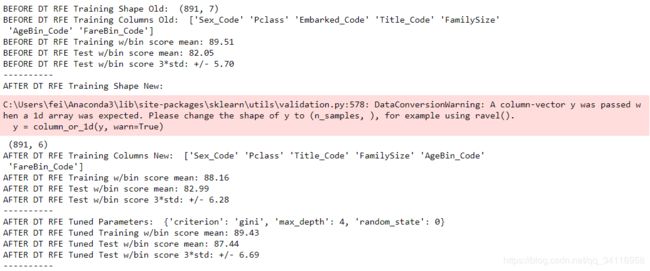
由结果可知特征选择后少了Embarked特征值，结果比特征选择前略微增大。
集成模型
既然可以使用集成模型中的投票分类器为何还要用单一的模型呢，接下来使用投票分类器进行建模。
投票分类器原理是使用多个算法模型进行建模，其有两种决策方式，Hard和soft，前者为少数服从多数原则，后者为权值投票方式。

vote_est = [
    #Ensemble Methods
    ('ada', ensemble.AdaBoostClassifier()),
    ('bc', ensemble.BaggingClassifier()),
    ('etc',ensemble.ExtraTreesClassifier()),
    ('gbc', ensemble.GradientBoostingClassifier()),
    ('rfc', ensemble.RandomForestClassifier()),

    #Gaussian Processes
    ('gpc', gaussian_process.GaussianProcessClassifier()),
    
    #GLM
    ('lr', linear_model.LogisticRegressionCV()),
    
    #Navies Bayes
    ('bnb', naive_bayes.BernoulliNB()),
    ('gnb', naive_bayes.GaussianNB()),
    
    #Nearest Neighbor
    ('knn', neighbors.KNeighborsClassifier()),
    
    #SVM
    ('svc', svm.SVC(probability=True)),
    
    #xgboost
   ('xgb', XGBClassifier())

]
#Hard Vote or majority rules   Hard投票或少数服从多数原则
vote_hard = ensemble.VotingClassifier(estimators = vote_est , voting = 'hard')
vote_hard_cv = model_selection.cross_validate(vote_hard, data1[data1_x_bin], data1[Target], cv = cv_split,return_train_score=True)
vote_hard.fit(data1[data1_x_bin], data1[Target])

print("Hard Voting Training w/bin score mean: {:.2f}". format(vote_hard_cv['train_score'].mean()*100)) 
print("Hard Voting Test w/bin score mean: {:.2f}". format(vote_hard_cv['test_score'].mean()*100))
print("Hard Voting Test w/bin score 3*std: +/- {:.2f}". format(vote_hard_cv['test_score'].std()*100*3))
print('-'*10)


#Soft Vote or weighted probabilities
vote_soft = ensemble.VotingClassifier(estimators = vote_est , voting = 'soft')
vote_soft_cv = model_selection.cross_validate(vote_soft, data1[data1_x_bin], data1[Target], cv = cv_split, return_train_score=True)
vote_soft.fit(data1[data1_x_bin], data1[Target])

print("Soft Voting Training w/bin score mean: {:.2f}". format(vote_soft_cv['train_score'].mean()*100)) 
print("Soft Voting Test w/bin score mean: {:.2f}". format(vote_soft_cv['test_score'].mean()*100))
print("Soft Voting Test w/bin score 3*std: +/- {:.2f}". format(vote_soft_cv['test_score'].std()*100*3))
print('-'*10)

结果中该方法似乎效果并不好，这里只是让大家了解该分类方法。
以上只是采用模型中的默认参数来进行投票分类，接下来对多个模型进行微调，让后再进行投票分类，注意接下来可能会消耗些时间。

#对集成模型进行超参数微调
import time
grid_n_estimator = [10, 50, 100, 300]
grid_ratio = [.1, .25, .5, .75, 1.0]
grid_learn = [.01, .03, .05, .1, .25]
grid_max_depth = [2, 4, 6, 8, 10, None]
grid_min_samples = [5, 10, .03, .05, .10]
grid_criterion = ['gini', 'entropy']
grid_bool = [True, False]
grid_seed = [0]


grid_param = [
            [{
            #AdaBoostClassifier 
            'n_estimators': grid_n_estimator, #default=50
            'learning_rate': grid_learn, #default=1
            #'algorithm': ['SAMME', 'SAMME.R'], #default=’SAMME.R
            'random_state': grid_seed
            }],
       
    
            [{
            #BaggingClassifier 
            'n_estimators': grid_n_estimator, #default=10
            'max_samples': grid_ratio, #default=1.0
            'random_state': grid_seed
             }],

    
            [{
            #ExtraTreesClassifier
            'n_estimators': grid_n_estimator, #default=10
            'criterion': grid_criterion, #default=”gini”
            'max_depth': grid_max_depth, #default=None
            'random_state': grid_seed
             }],


            [{
            #GradientBoostingClassifier 
            #'loss': ['deviance', 'exponential'], #default=’deviance’
            'learning_rate': [.05], #default=0.1 -- 12/31/17 set to reduce runtime -- The best parameter for GradientBoostingClassifier is {'learning_rate': 0.05, 'max_depth': 2, 'n_estimators': 300, 'random_state': 0} with a runtime of 264.45 seconds.
            'n_estimators': [300], #default=100 -- 12/31/17 set to reduce runtime -- The best parameter for GradientBoostingClassifier is {'learning_rate': 0.05, 'max_depth': 2, 'n_estimators': 300, 'random_state': 0} with a runtime of 264.45 seconds.
            #'criterion': ['friedman_mse', 'mse', 'mae'], #default=”friedman_mse”
            'max_depth': grid_max_depth, #default=3   
            'random_state': grid_seed
             }],

    
            [{
            #RandomForestClassifier 
            'n_estimators': grid_n_estimator, #default=10
            'criterion': grid_criterion, #default=”gini”
            'max_depth': grid_max_depth, #default=None
            'oob_score': [True], #default=False -- 12/31/17 set to reduce runtime -- The best parameter for RandomForestClassifier is {'criterion': 'entropy', 'max_depth': 6, 'n_estimators': 100, 'oob_score': True, 'random_state': 0} with a runtime of 146.35 seconds.
            'random_state': grid_seed
             }],
    
            [{    
            #GaussianProcessClassifier
            'max_iter_predict': grid_n_estimator, #default: 100
            'random_state': grid_seed
            }],
        
    
            [{
            #LogisticRegressionCV 
            'fit_intercept': grid_bool, #default: True
            #'penalty': ['l1','l2'],
            'solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga'], #default: lbfgs
            'random_state': grid_seed
             }],
            
    
            [{
            #BernoulliNB 
            'alpha': grid_ratio, #default: 1.0
             }],
    
    
            #GaussianNB - 
            [{}],
    
            [{
            #KNeighborsClassifier 
            'n_neighbors': [1,2,3,4,5,6,7], #default: 5
            'weights': ['uniform', 'distance'], #default = ‘uniform’
            'algorithm': ['auto', 'ball_tree', 'kd_tree', 'brute']
            }],
            
    
            [{
            #SVC 
            #'kernel': ['linear', 'poly', 'rbf', 'sigmoid'],
            'C': [1,2,3,4,5], #default=1.0
            'gamma': grid_ratio, #edfault: auto
            'decision_function_shape': ['ovo', 'ovr'], #default:ovr
            'probability': [True],
            'random_state': grid_seed
             }],

    
            [{
            #XGBClassifier 
            'learning_rate': grid_learn, #default: .3
            'max_depth': [1,2,4,6,8,10], #default 2
            'n_estimators': grid_n_estimator, 
            'seed': grid_seed  
             }]   
        ]

start_total = time.perf_counter() 
for clf, param in zip (vote_est, grid_param): 

    #print(clf[1]) #vote_est is a list of tuples, index 0 is the name and index 1 is the algorithm
    #print(param)
    
    
    start = time.perf_counter()        
    best_search = model_selection.GridSearchCV(estimator = clf[1], param_grid = param, cv = cv_split, scoring = 'roc_auc')
    best_search.fit(data1[data1_x_bin], data1[Target])
    run = time.perf_counter() - start

    best_param = best_search.best_params_
    print('The best parameter for {} is {} with a runtime of {:.2f} seconds.'.format(clf[1].__class__.__name__, best_param, run))
    clf[1].set_params(**best_param) 


run_total = time.perf_counter() - start_total
print('Total optimization time was {:.2f} minutes.'.format(run_total/60))

print('-'*10)

grid_hard = ensemble.VotingClassifier(estimators = vote_est , voting = 'hard')
grid_hard_cv = model_selection.cross_validate(grid_hard, data1[data1_x_bin], data1[Target], cv  = cv_split)
grid_hard.fit(data1[data1_x_bin], data1[Target])

print("Hard Voting w/Tuned Hyperparameters Training w/bin score mean: {:.2f}". format(grid_hard_cv['train_score'].mean()*100)) 
print("Hard Voting w/Tuned Hyperparameters Test w/bin score mean: {:.2f}". format(grid_hard_cv['test_score'].mean()*100))
print("Hard Voting w/Tuned Hyperparameters Test w/bin score 3*std: +/- {:.2f}". format(grid_hard_cv['test_score'].std()*100*3))
print('-'*10)

#对微调后的模型使用投票分类器
#Soft Vote or weighted probabilities w/Tuned Hyperparameters
grid_soft = ensemble.VotingClassifier(estimators = vote_est , voting = 'soft')
grid_soft_cv = model_selection.cross_validate(grid_soft, data1[data1_x_bin], data1[Target], cv  = cv_split)
grid_soft.fit(data1[data1_x_bin], data1[Target])

print("Soft Voting w/Tuned Hyperparameters Training w/bin score mean: {:.2f}". format(grid_soft_cv['train_score'].mean()*100)) 
print("Soft Voting w/Tuned Hyperparameters Test w/bin score mean: {:.2f}". format(grid_soft_cv['test_score'].mean()*100))
print("Soft Voting w/Tuned Hyperparameters Test w/bin score 3*std: +/- {:.2f}". format(grid_soft_cv['test_score'].std()*100*3))
print('-'*10)

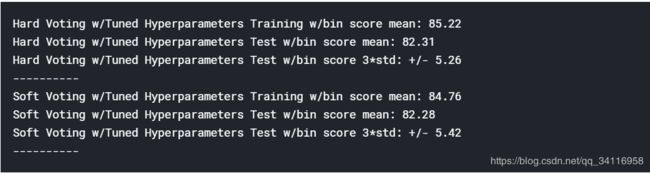
结果可知微调后的效果好像并不明显，不过在这里也算对该投票分类有所了解。
终于到最后一步了，对测试集进行训练提交。

print(test_data.info())
print("-"*10)
test_data['Survived'] = grid_hard.predict(test_data[data1_x_bin])
submit = test_data[['PassengerId','Survived']]
submit.to_csv("predictions/result", index=False)

print('Validation Data Distribution: \n', test_data['Survived'].value_counts(normalize = True))
submit.sample(10)

采用最后训练的模型grid_hard模型进行测试，预测结果存储于result中，提交。

最终的提交分数为0.7655，emmm,搞了这么半天分数好像很低?，说明还有很大的进步空间啊，同时在绘图模型方面应该都涉及到了，剩下的就是靠自己去摸索了。