卡尔曼滤波MatLab实例一:房间温度
卡尔曼滤波简介
最近接触到卡尔曼滤波,查阅了图书馆以及网上的一些资料,稍微有点收获,在此记录一下,方便之后用到。
我主要参考了以下内容:
①https://blog.csdn.net/u010720661/article/details/63253509
这一篇博客讲的非常形象,强烈推荐先看;
博主翻译自:
http://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
②https://blog.csdn.net/victor_zy/article/details/82862904
卡尔曼滤波的一种推导,类似的推导博客上有很多,可以都来了解一下;
③《卡尔曼滤波原理及应用——MatLab仿真》黄小平 王岩
有线性卡尔曼滤波、扩展卡尔曼滤波、无迹卡尔曼滤波等很多在MatLab上实现的例子。
我理解的卡尔曼滤波的作用就是处理噪声,通过状态方程预测,观测修正的的方法,把噪声的影响降到最低。卡尔曼滤波中最简单的情况是线性卡尔曼滤波,应用于线性系统,即系统的状态方程可以表示成如下形式的系统:
![]()
其中x、u、w分别为系统的状态变量、控制变量、输入噪声;A、B、C分别为状态转移矩阵、控制矩阵、噪声控制矩阵。
系统的观测方程可以表示成如下形式:
![]()
其中y、v为传感器观测到的变量、观测噪声;H为观测矩阵。
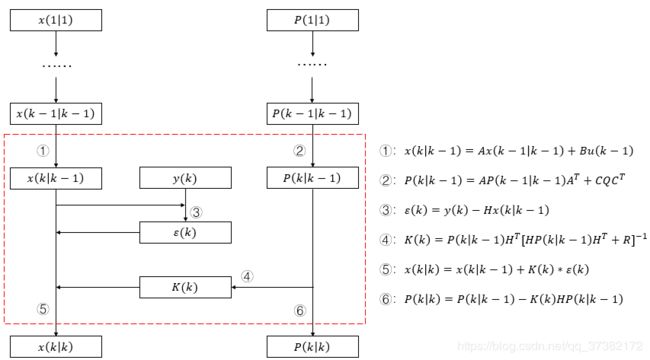
为了方便理解和代码实现,我把卡尔曼滤波的迭代过程整理成以下的形式。红色虚线框展示了由(k-1)到(k)的实现过程。其中P为x的协方差矩阵,K为卡尔曼增益,?为新息序列(观测值与预测的观测值之差),Q为输入噪声的协方差矩阵,R为观测噪声的协方差矩阵。沿用了推导中(k|k)的记号,含义如下:x(k|k-1)为由k-1时刻预测的k时刻的值,x(k|k)为由k时刻观测量修正后的k时刻的值,P为对应x的协方差矩阵。
MatLab实例:房间温度
问题描述为有一个房间,里面有一个温度计,还有一个人想要估计房间的温度。问题分析如下:
①状态变量只有一个温度,为一维问题,上述矩阵其实都是标量;
②房间没有开空调或者通暖气,不存在刻意驱使房间温度变化的力量,所以A=1,B=0,u=0;
③房间没有完全密封,温度会受到随机的太阳照射和通风的微量影响,假设温度变动w服从高斯分布,取其方差为0.09,即Q=0.09;
④温度计和房间温度均以摄氏度为单位,所以测量矩阵H=1;
⑤温度计存在随机的测量误差,假设测温误差服从高斯分布,取其方差为0.25,即R=0.25;
⑥假设初始时实际温度为25℃,迭代初始温度也取25℃,并假设此前卡尔曼滤波得到的温度方差为0(也可以取其他值),所以P=0。
代码如下:
close all; clear
% Temperature in a room
%---------------------------------
% define time span
dt = 1; % unit: s
n = 100;
% define x
x_act = zeros(1,n); %actual x
x_cor = zeros(1,n); %correctional x
x_pre = zeros(1,n); %predicted x
x_obs = zeros(1,n); %observed x
t = zeros(1,n);
% define Kalman Gain
K = 0;
epsilon = 0;
% define Matrix and Vector A B...
A = 1;
B = 0;
C = 1;
H = 1;
% define w v u
Q = 0.09;
w = normrnd(0,sqrt(Q),1,n);
R = 0.25;
v = normrnd(0,sqrt(R),1,n);
u = zeros(1,n);
% initialize
x_act(1) = 25;
x_cor(1) = 25;
x_obs(1) = 25;
x_pre(1) = 25;
t(1) = dt;
P_cor = 0;
P_pre = 0;
%---------------------------------
% loop
for k = 2:n
% predict x
t(k) = t(k-1)+dt;
x_pre(k) = A*x_cor(k-1)+B*u(k-1);
x_act(k) = x_pre(k)+C*w(k);
x_obs(k) = H*x_act(k)+v(k);
P_pre = A*P_cor*A'+C*Q*C';
% correct
epsilon = x_obs(k)-H*x_pre(k);
K = P_pre*H'/(H*P_pre*H'+R);
x_cor(k) = x_pre(k)+K*epsilon;
P_cor = P_pre-K*H*P_pre;
end
%---------------------------------
% analyze
figure;
plot(t,x_act,'k-',t,x_pre,'g--',t,x_obs,'b--',t,x_cor,'r-');
legend('Actual T','Predicted T','Observed T','Correctional T','Location','best');
title('KF example: Tempurate');
xlabel('Time/s');
ylabel('Tempurate/^oC');
figure;
error_KF = x_cor-x_act;
error_obs = x_obs-x_act;
error_pre = x_pre-x_act;
plot(t,error_KF,'r-',t,error_pre,'g-',t,error_obs,'b-');
legend('KF Error','Predict Error','Observe Error','Location','best');
title('KF example: Tempurate');
xlabel('Time/s');
ylabel('Error/^oC');
运行得到的结果如下:(温度曲线和误差曲线)
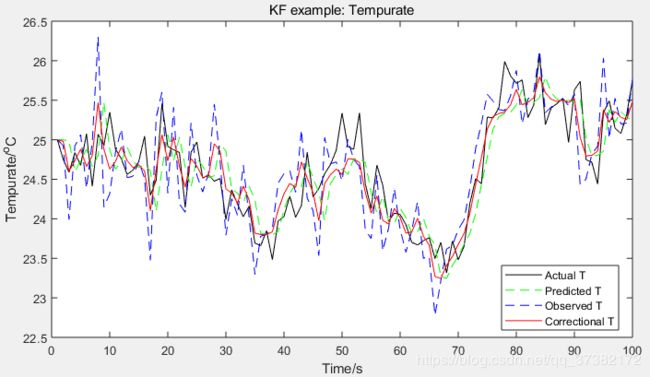
黑色线为实际温度曲线,红色线为卡尔曼滤波修正后的温度曲线。

个人理解:
①卡尔曼滤波是通过让状态变量的方差最小,实现最优估计的,方差信息包含在协方差矩阵中,所以要不断地更新协方差矩阵P;
②卡尔曼滤波中的Q和R可以描述输入噪声和测量噪声的性状,可以影响修正过程中预测和观测所占的比重,因此根据噪声和传感器情况确定合适的Q和R是十分重要的。