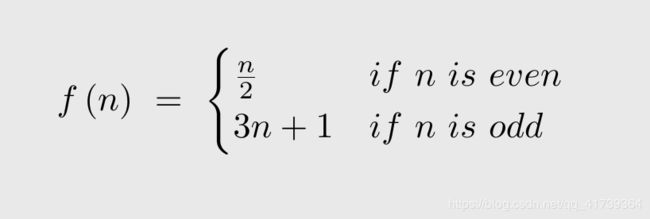尚未解决的10个最困难的数学问题
《尚未解决的10个最困难的数学问题》
- 1.科拉兹猜想
- 2.哥德巴赫猜想
- 3.双素猜想
- 4.黎曼假设
- 5.Birch和Swinnerton-Dyer猜想
- 6.接吻数问题
- 7.难题
- 8.大型基数计划
- 9.与? + e有何关系?
- 10. ?理性吗?
尚未解决的10个最困难的数学问题
世界上最聪明的人无法破解他们。也许您会有更好的运气。
对于我们在数学领域取得的最新进展,例如超级计算机如何最终解决了困扰数学家65年的“三次求和”问题,我们一直在努力进行计算,以寻求更深入的数值知识。几个世纪以来,一些数学问题一直在挑战着我们,尽管像随后的那些大脑破坏者似乎不可能,但最终有人一定会解决它们。也许。
现在,先解决男人,女人和机器已知的最棘手的数学问题。
1.科拉兹猜想
本月初,得益于多产的数学家陶伦斯·陶(Terence Tao),有关这个已有82年历史的问题的新闻爆出。尽管陶行长的突破故事是个好消息,但问题仍未完全解决。
关于Collatz猜想的更新:上面显示的是函数f(n)的全部内容,该函数取偶数并将其减半,而奇数取三倍,然后加到1。取任何自然数,应用f,然后一次又一次地应用f。我们最终检查过的每个数字最终都会落在1上。猜想是,所有自然数都是如此。
陶最近的工作在某种程度上是对科拉兹猜想的一个接近解决方案。但是,正如他随后解释的那样,他的方法很可能无法适应该问题的完整解决方案。因此,我们可能会为此工作数十年。
猜想属于数学学科,称为动态系统,或者是研究以半可预测的方式随时间变化的情况。它看起来像一个简单,无害的问题,但这就是它与众不同的原因。为什么这样一个基本问题很难回答?它是我们理解的基准;一旦解决,我们就可以处理更复杂的事情。
对动力系统的研究可能会比今天任何人所想像的都要强大。但是,我们需要解决科拉兹猜想才能使该学科蓬勃发展。
2.哥德巴赫猜想
数学上最大的未解之谜之一也很容易写。哥德巴赫的猜想是:“每个偶数(大于2)是两个质数的和。”您在脑海中检查了较小的数字:18是13 + 5,而42是23 + 19。计算机已经检查了猜想中的数值是否达到一定程度。但是我们需要证明所有自然数。
哥德巴赫猜想源于1742年德国数学家克里斯蒂安·哥德巴赫(Christian Goldbach)和传奇的瑞士数学家莱昂哈德·欧拉(Leonhard Euler)之间的信件,被认为是数学史上最伟大的猜想之一。正如欧拉所说:“尽管我无法证明它,但我仍将其视为完全确定的定理。”
欧拉可能已经感觉到是什么使直觉上的问题难以解决。当您查看较大的数字时,它们有更多的质数之和而不是更少的写法。就像3 + 5是将8分解成两个素数的唯一方法一样,但是42可以分解成5 + 37、11 + 31、13 + 29和19 + 23。因此,感觉像哥德巴赫的猜想对于很多人来说都是轻描淡写的。
尽管如此,直到今天,数学家仍无法证明所有数字都是猜想的。它是所有数学中最古老的开放式问题之一。
3.双素猜想
孪生素数猜想与哥德巴赫猜想一道,在数学学科中最著名,称为数论,即对自然数及其性质的研究,通常涉及素数。由于您从小学起就已经知道这些数字,因此陈述这些猜测很容易。
当两个素数之差为2时,它们称为孪生素数。因此11和13是双质数,而599和601都是双质数。现在,第1天数论事实表明存在无限多个质数。那么,有无限多个双素数吗?双生素数猜想是肯定的。
让我们更深入一点。一对双素数中的第一个素数总是比6的倍数小1。因此,第二个双素数素数总是比6的倍数大1。您可以理解为什么,如果您准备好遵循一些数论。
2之后的所有素数都是奇数。偶数始终比6的倍数大0、2或4,而奇数始终比6的倍数大1、3或5。好吧,这三种奇数可能性之一引起了问题。如果数字3大于6的倍数,则其系数为3。系数为3表示数字不是质数(唯一的例外是3本身)。这就是为什么每个第三个奇数都不是质数的原因。
那段时间过后你的头怎么样?现在,想象一下在过去170年中试图解决此问题的每个人的头痛。
好消息是,过去十年来我们取得了可喜的进展。数学家已经设法解决越来越接近的孪生素数猜想。这就是他们的想法:难于证明有多少个质数相差2?如何证明有无数个质数相差70,000,000的质数。2013年,新罕布什尔大学的Yitang Zhang巧妙地证明了这一点。
在过去的六年中,数学家一直在用张的证明来提高这个数字,从数百万减少到数百。将其降低到2将是Twin Prime Conjecture的解决方案。根据一些细微的技术假设,我们得出的最接近的数字是6。时间将证明从6到2的最后一步是否即将到来,或者该最后一步是否会挑战数学家数十年。
4.黎曼假设
当今的数学家可能会同意,黎曼假设是所有数学中最重要的开放问题。它是七个“ 千年奖”问题之一,并为其解决方案悬赏一百万美元。它对数学的各个分支都有着深远的影响,但是它也很简单,我们可以在这里解释其基本概念。
上图中编写了一个称为Riemann zeta函数的函数。
对于每个s,此函数给出一个无穷大的和,这需要一些基本演算才能求出s的最简单值。例如,如果s = 2,则?(s)是众所周知的级数 1 + 1/4 + 1/9 + 1/16 +…,这奇怪地加起来恰好是?² / 6。当s是一个复数(一个看起来像a +b?的复数)时,使用虚数?查找?是很棘手的。
如此棘手,实际上,它已成为最终的数学问题。具体地说,黎曼假设大约是当?(s)= 0时;正式声明是:“黎曼zeta函数的每个非平凡零都具有实部1/2。”在复数平面上,这意味着该函数沿特殊的垂直线具有一定的行为。您可以在上面的函数的可视化效果中看到这一点-它沿着彩虹和红色的边界。假设是行为无限地沿着那条线继续。
假设和zeta函数来自德国数学家Bernhard Riemann,他们在1859年对其进行了描述。Riemann在研究素数及其分布时开发了它们。自从160年来,我们对质数的理解一直在蓬勃发展,而黎曼(Riemann)从未想象过超级计算机的力量。但是,缺乏解决黎曼假设的方法是一个重大的挫折。
如果黎曼假设在明天得到解决,它将掀起进一步发展的雪崩。这将是整个数论与分析学科的重大新闻。直到那时,黎曼假设仍然是数学研究之河上最大的水坝之一。
5. Birch和Swinnerton-Dyer猜想
该桦木和斯维讷代尔猜想是另一个六项未解千禧年大奖难题,而且它是唯一另外一个我们可以用简单的英语远程描述。此猜想涉及称为椭圆曲线的数学主题。
当我们最近撰写有关已解决的最棘手的数学问题的文章时,我们提到了20世纪数学的最大成就之一:费马最后定理的解决方案。它由安德鲁·威尔斯爵士使用椭圆曲线解决。因此,您可以称其为非常强大的数学新分支。
简而言之,椭圆曲线是一种特殊的功能。它们采用看起来没有威胁的形式y²=x³+ ax + b。事实证明,像这样的函数具有某些属性,这些属性使人们对诸如代数和数论之类的数学主题有了深刻的了解。
英国数学家Bryan Birch和Peter Swinnerton-Dyer在1960年代发展了他们的猜想。它的确切陈述是非常技术性的,并且经过多年的发展。这种演变的主要管理者之一就是威尔斯。要了解其当前状态和复杂性,请查看Wells在2006年发布的这一著名更新。
6.接吻数问题
数学中的一类广泛的问题称为“ 球体堆积问题”。它们的范围从纯粹的数学到实际应用,通常将数学术语引入在给定空间中堆叠多个球体(例如杂货店的水果)的想法。本研究中的某些问题具有完整的解决方案,而一些简单的问题则使我们感到困惑,例如“接吻数问题”。
当一堆球体堆积在某个区域中时,每个球体都有一个“接吻数”,即它所接触的其他球体的数量;如果您要触摸6个相邻的球体,那么您的接吻数为6。一堆球体将具有一个平均接吻数,这有助于从数学上描述情况。但是有关接吻号码的基本问题尚未得到解答。
首先,要注意尺寸。尺寸在数学上有特定含义:它们是独立的坐标轴。x轴和y轴显示坐标平面的二维。当科幻节目中的角色说他们要去一个不同的维度时,这在数学上是没有意义的。您无法转到x轴。
一维物体是线,二维物体是平面。对于这些较低的数字,数学家已经证明了这么多尺寸的球体的最大可能接吻数。在1-D线上时为2,即一个球在您的左侧,另一个球在您的右侧。尽管直到1950年代才有3个维度的确切数字的证明。
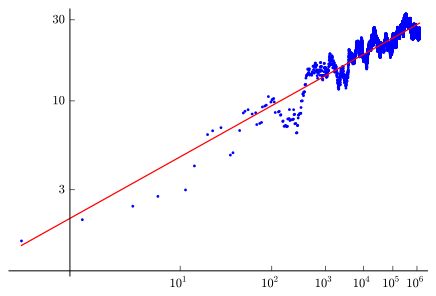
超过3个维度,接吻问题大部分尚未解决。数学家慢慢地将可能性缩小到了多达24个维度的相当窄的范围,其中一些确切已知,如您在此图表中所见。对于较大的数字或一般形式,问题是普遍存在的。完整解决方案有几个障碍,包括计算限制。因此,预计未来几年将在此问题上取得逐步进展。
7.难题
最简单的“ 解开问题”版本已解决,因此该故事已经取得了一些成功。解决问题的完整版本将是更大的胜利。
您可能还没有听说过数学科目“结理论”。几乎没有高中和几所大学都教过它。这个想法是尝试将形式上的数学思想(如证明)应用于打结(例如……),将鞋子绑在一起。
例如,您可能知道如何打结“方结”和“ gr结”。它们的步骤相同,只是从方结到奶奶结的扭转是相反的。但是,您能证明那些结是不同的吗?结理论家可以。
结理论家的圣杯问题是一种算法,该算法可以确定是否纠结了一些纠结的乱七八糟的东西,或者它是否可以解开。好消息是,这已经完成了!在过去的20年中,已经为此编写了几种计算机算法,其中一些甚至使该过程更加活跃。
未知问题仍然存在的地方是计算的。用技术术语来说,众所周知“解结问题”在NP中,而我们不知道它是否在P中。这大致意味着我们知道我们的算法能够解开任何复杂的结,但是随着它们变得越来越复杂,它开始花费很长时间。目前。
如果有人提出了一种算法,该算法可以在所谓的多项式时间内消除任何打结,那么就可以完全解决“打结问题”。另一方面,有人可以证明这是不可能的,并且“解开问题”的计算强度不可避免地是深远的。最终,我们会找到答案。
8.大型基数计划
如果您从未听说过大型红衣主教,请准备学习。在19世纪末,一位名叫Georg Cantor的德国数学家发现无穷大的大小不同。实际上,某些无穷集在深度数学上比其他无穷集具有更多的元素,而Cantor证明了这一点。
有第一个无穷大,最小无穷大,记为ℵ₀。那是希伯来语字母aleph;它的读数为“ aleph-零”。它是一组自然数的大小,因此被写为|ℕ| =ℵ₀。
接下来,一些常见集合大于大小ℵ₀。Cantor证明的主要示例是实数集更大,用|ℝ|>ℵ₀表示。但是,实际收益并不大。我们才刚刚开始使用无限大小。
对于真正的大东西,数学家不断发现越来越大的尺寸,或者我们称之为大红衣主教。这是一个纯数学的过程,如下所示:有人说:“我想到了一个红衣主教,我可以证明这个红衣主教比所有已知的红衣主教还大。”然后,如果他们的证明是好的,那就是新的最大的已知主教。直到有人提出更大的建议。
在整个20世纪,已知的大型枢机主教的边界稳步向前发展。现在甚至有一个美丽的维基百科,以著名的红衣主教命名,以纪念Cantor。那么,这将永远结束吗?答案是肯定的,尽管它变得非常复杂。
从某种意义上说,大型主教层级的顶端已可见。一些定理已经被证明,对大红衣主教的可能性施加了某种限制。但是仍然存在许多悬而未决的问题,新的枢机主教已在2019年确定下来。很可能我们会在未来几十年内发现更多的枢机。希望我们最终能得到所有大型红衣主教的详尽清单。
9. 与? + e有何关系?
鉴于我们对数学中最著名的两个常数?和e所了解的一切,这真让人惊讶,将它们加在一起时我们迷失了多少。
这个奥秘全是关于代数实数的。定义:如果实数是某些具有整数系数的多项式的根,则实数是代数的。例如,x²-6是具有整数系数的多项式,因为1和-6是整数。x²-6= 0的根是x =√6和x =-√6,这意味着√6和-√6是代数数。
所有有理数和有理数的根都是代数的。因此,可能感觉“最”的实数是代数的。原来实际上是相反的。代数的反义词是超验的,事实证明,几乎所有实数都是超验的,因为“几乎所有”的某些数学含义都是如此。那么谁是代数的,谁是超验的呢?
实数real可以追溯到古代数学,而数字e自17世纪以来一直存在。您可能已经听说过这两种方法,并且您认为我们知道有关它们的每个基本问题的答案,对吗?
好吧,我们确实知道?和e都是先验的。但是不知道? + e是代数的还是超验的。同样,我们不了解?e,? / e及其它们的其他简单组合。因此,关于我们几千年来知道的数字仍然存在着令人难以置信的基本问题,这些问题仍然是神秘的。
10. ?理性吗?
这是另一个很容易编写但很难解决的问题。您只需要记住有理数的定义。
有理数可以p / q的形式编写,其中p和q是整数。因此42和-11/3是有理数,而?和√2不是有理数。这是一个非常基本的属性,因此您认为我们可以轻松判断数字何时是有理数,对吗?
满足Euler-Mascheroni常数 ?,它是小写的希腊伽马。它是一个实数,大约为0.5772,其闭合形式并不难看。它看起来像上面的图片。
在这些符号上加上单词的流畅方式是“伽马是谐波序列和自然对数之差的极限。”因此,它是两个非常容易理解的数学对象的组合。它具有其他简洁的封闭形式,并以数百种公式出现。
但是不知何故,我们甚至都不知道?是否合理。我们已经将其计算为半万亿位数,但没有人能证明它是否合理。普遍的预测是?是非理性的。与前面的示例? + e一起,我们还有另一个问题,即众所周知的数字的简单属性,甚至无法回答。