介绍一下如何用一维卷积来做序列模型,基于Keras的详细代码解析
点击上方“AI公园”,关注公众号,选择加“星标“或“置顶”
导读作者:Nils Ackermann
编译:ronghuaiyang
许多文章关注二维卷积神经网络,主要是用于图像相关的问题。一维cnn在一定程度上也包括在内了,例如自然语言处理(NLP)。但是,对于你可能面临的其他机器学习问题,很少有文章提供关于如何构建1D CNN的解释性的操作。本文试图弥补这一差距。
介绍
许多文章关注二维卷积神经网络,主要是用于图像相关的问题。一维cnn在一定程度上也包括在内了,例如自然语言处理(NLP)。但是,对于你可能面临的其他机器学习问题,很少有文章提供关于如何构建1D CNN的解释性的操作。本文试图弥补这一差距。
什么时候使用1D CNN?
CNN可以很好地识别数据中的简单模式,然后将其用于在更高的层中形成更复杂的模式。当你希望从整个数据集中较短(固定长度)的片段中获得特征,并且该特征在片段中的位置相关性不高时,一维CNN非常有效。
这可以很好地应用于分析传感器数据的时间序列(如陀螺仪或加速度计数据)。它也适用于分析任何类型的信号数据在固定长度的周期(如音频信号)。另一个应用程序是NLP(尽管这里LSTM更有前途,因为单词的接近程度可能并不总是可训练模式的良好指示器)。
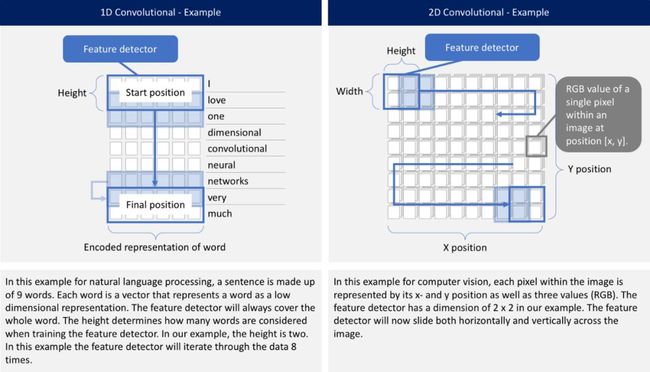
1D CNN和2D CNN之间有什么差别?
无论是一维、二维还是三维,CNNs都具有相同的特性,并遵循相同的方法。关键的区别在于输入数据的维数,以及特征检测器(或过滤器)如何在数据之间滑动:
问题描述
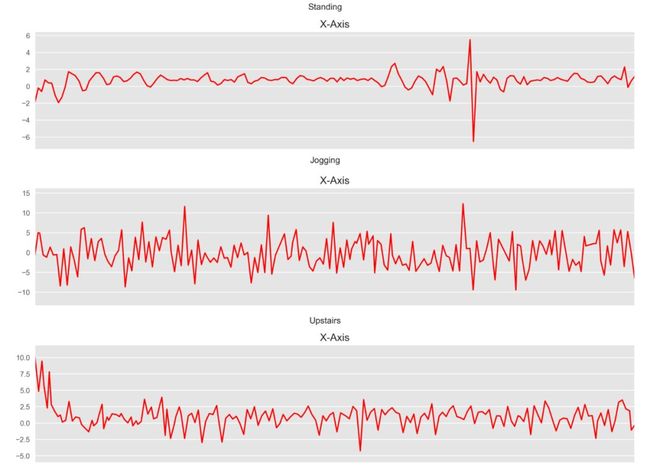
在这篇文章中,我们将专注于自于智能手机的时间切片的加速度计和传感器数据。根据x轴、y轴和z轴的加速度计数据,1D CNN可以预测用户正在进行的活动类型(如“散步”、“慢跑”或“站立”)。对于各种活动,数据的每个时间间隔都类似于此。
如何在Python中构建1D CNN?
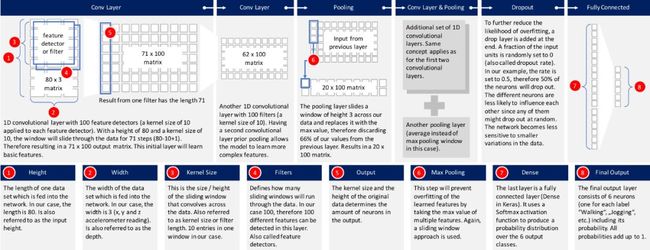
有许多标准的CNN模型可用。我选择了Keras网站上描述的一个模型(https://keras.io/getting-started/sequential-model-guide/),并对其进行了轻微修改,以适应上面描述的问题。下图提供了构建模型的高层概览。每一层都将作进一步解释。
我们先看看Python代码:
model_m = Sequential()
model_m.add(Reshape((TIME_PERIODS, num_sensors), input_shape=(input_shape,)))
model_m.add(Conv1D(100, 10, activation='relu', input_shape=(TIME_PERIODS, num_sensors)))
model_m.add(Conv1D(100, 10, activation='relu'))
model_m.add(MaxPooling1D(3))
model_m.add(Conv1D(160, 10, activation='relu'))
model_m.add(Conv1D(160, 10, activation='relu'))
model_m.add(GlobalAveragePooling1D())
model_m.add(Dropout(0.5))
model_m.add(Dense(num_classes, activation='softmax'))
print(model_m.summary())运行此代码将产生如下深度神经网络:
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
reshape_45 (Reshape) (None, 80, 3) 0
_________________________________________________________________
conv1d_145 (Conv1D) (None, 71, 100) 3100
_________________________________________________________________
conv1d_146 (Conv1D) (None, 62, 100) 100100
_________________________________________________________________
max_pooling1d_39 (MaxPooling (None, 20, 100) 0
_________________________________________________________________
conv1d_147 (Conv1D) (None, 11, 160) 160160
_________________________________________________________________
conv1d_148 (Conv1D) (None, 2, 160) 256160
_________________________________________________________________
global_average_pooling1d_29 (None, 160) 0
_________________________________________________________________
dropout_29 (Dropout) (None, 160) 0
_________________________________________________________________
dense_29 (Dense) (None, 6) 966
=================================================================
Total params: 520,486
Trainable params: 520,486
Non-trainable params: 0
_________________________________________________________________
None让我们深入每一层看看发生了什么:
输入数据:数据经过预处理,每个数据记录包含80个时间片(数据以20赫兹采样率记录,因此每个时间间隔包含加速度计读取的4秒数据)。在每个时间间隔内,存储x轴、y轴和z轴的三个加速度计值。这就得到了一个80x3矩阵。由于我通常在iOS中使用神经网络,所以数据必须作为长度为240的平面向量传递到神经网络中。网络的第一层必须将其重塑为原来的形状,即80 x 3。
第一个一维CNN层: 一个高度为10(也称为内核大小)的过滤器(或也称为特征检测器)。只定义一个过滤器将允许神经网络学习第一层中的一个单一特征。这可能还不够,因此我们将定义100个过滤器。这允许我们在网络的第一层训练100个不同的特征。第一个神经网络层的输出是一个71 x 100的神经元矩阵。输出矩阵的每一列包含一个过滤器的权重。根据定义的内核大小和考虑输入矩阵的长度,每个过滤器将包含71个权重。
第二个一维CNN层:第一个CNN的结果将被输入第二个CNN层。我们将再次定义100个不同的过滤器在这个级别上进行训练。按照与第一层相同的逻辑,输出矩阵的大小将为62 x 100。
最大池化层:通常在CNN层之后使用池化层,以降低输出的复杂度,防止数据过拟合。在我们的示例中,我们选择了尺寸为3。这意味着该层的输出矩阵的大小仅为输入矩阵的三分之一。
第三和第四个一维CNN层:下面是一维CNN层的另一个序列,以便学习更高层次的特征。这两层之后的输出矩阵是一个2x160矩阵。
平均池化层:多一个池化层,进一步避免过拟合。这次不是取最大值,而是取神经网络中两个权值的平均值。输出矩阵的大小为1 x 160个神经元。每个特征检测器在这一层的神经网络中只剩下一个权值。
Dropout层: Dropout层将随机分配权值0给网络中的神经元。因为我们选择了0.5的概率,50%的神经元将获得0权值。通过这种操作,网络对数据中较小的变化不那么敏感。因此,它应该进一步提高我们对不可见数据的准确性。这一层的输出仍然是1×160个神经元矩阵。
使用Softmax激活的全连接层:最后一层将高度160的向量减少到6,因为我们要预测6个类(“慢跑”、“坐下”、“行走”、“站立”、“上楼”、“下楼”)。这由一个矩阵乘法完成。使用Softmax作为激活函数。它使神经网络的所有6个输出加起来等于1。因此,输出值将表示这六个类中的每个类的概率。
训练和测试神经网络
下面是Python代码,用于训练批处理大小为400、训练和验证大小为80到20的模型。
callbacks_list = [
keras.callbacks.ModelCheckpoint(
filepath='best_model.{epoch:02d}-{val_loss:.2f}.h5',
monitor='val_loss', save_best_only=True),
keras.callbacks.EarlyStopping(monitor='acc', patience=1)
]
model_m.compile(loss='categorical_crossentropy',
optimizer='adam', metrics=['accuracy'])
BATCH_SIZE = 400
EPOCHS = 50
history = model_m.fit(x_train,
y_train,
batch_size=BATCH_SIZE,
epochs=EPOCHS,
callbacks=callbacks_list,
validation_split=0.2,
verbose=1)该模型对训练数据的准确率达到97%。
...
Epoch 9/50
16694/16694 [==============================] - 16s 973us/step - loss: 0.0975 - acc: 0.9683 - val_loss: 0.7468 - val_acc: 0.8031
Epoch 10/50
16694/16694 [==============================] - 17s 989us/step - loss: 0.0917 - acc: 0.9715 - val_loss: 0.7215 - val_acc: 0.8064
Epoch 11/50
16694/16694 [==============================] - 17s 1ms/step - loss: 0.0877 - acc: 0.9716 - val_loss: 0.7233 - val_acc: 0.8040
Epoch 12/50
16694/16694 [==============================] - 17s 1ms/step - loss: 0.0659 - acc: 0.9802 - val_loss: 0.7064 - val_acc: 0.8347
Epoch 13/50
16694/16694 [==============================] - 17s 1ms/step - loss: 0.0626 - acc: 0.9799 - val_loss: 0.7219 - val_acc: 0.8107将其与测试数据进行比较,准确率为92%。
Accuracy on test data: 0.92
Loss on test data: 0.39考虑到我们使用的是一个标准的一维CNN模型,这是一个很好的数字。我们的模型在精确度、召回率和f1分上也得分很高。
precision recall f1-score support
0 0.76 0.78 0.77 650
1 0.98 0.96 0.97 1990
2 0.91 0.94 0.92 452
3 0.99 0.84 0.91 370
4 0.82 0.77 0.79 725
5 0.93 0.98 0.95 2397
avg / total 0.92 0.92 0.92 6584下面简要回顾一下这些分数的含义:
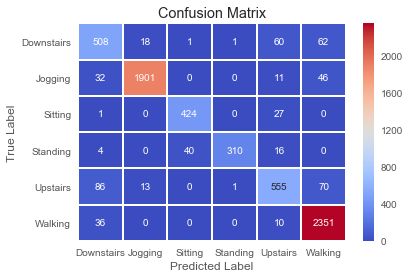
与测试数据相关联的混淆矩阵如下所示。
总结
在本文中,你可以看到如何使用1D CNN训练网络,演示了一个根据智能手机上的一组加速度计数据预测用户行为的示例。完整的Python代码可以在github:https://github.com/ni79ls/har-keras-cnn上找到。
英文原文:https://blog.goodaudience.com/introduction-to-1d-convolutional-neural-networks-in-keras-for-time-sequences-3a7ff801a2cf
![]()
请长按或扫描二维码关注本公众号
喜欢的话,请给我个好看吧!![]()