Kaggle项目实战1——Digit Recognizer——排名Top10%
一、kaggle介绍
Kaggle是一个大数据的众包平台,也是一个很好的项目实践场所。Kaggle的项目分为练习项目和奖励项目。今天写的Digit Recognizer属于练习项目,最后的结果只按照测试集的正确率计算排名,没有奖励。解决方案的python代码在Github开源平台上。
二、Digit Recognizer任务
此任务是在MNIST(一个带Label的数字像素集合)上训练一个数字分类器,训练集的大小为42000个training example,每个example是28*28=784个灰度像素值和一个0~9的label。最后的排名以在测试集合上的分类正确率为依据排名。
三、工具准备
这个项目在python环境下做,需要安装的库有ipython,numpy,matplotlib,pandas,scikit-learn,theano。在window环境下其中ipython,numpy,matplotlib,pandas库可以通过安装Canopy集成开发环境完成并且省去了环境变量的配置。Canpy的下载在这里,在校学生注册认证可以获得学术版本的Canopy。ipython负责提供交互式的开发调试环境,numpy负责科学计算库,matplotlib负责绘图和数据可视化,pandas库负责数据的转换和导入导出。scikit-learn是python下比较成熟的机器学习库,其文档多而规范。theano库是deeplearning的库,在Canopy中安装theano库需要在Canopy的Package Manager中事先安装libpython和mingw。
四、第一次尝试:Random Forest
一看是分类问题,第一个想法就是利用随机森林。随机森林本质是一种bagging的方法,其bagging的对象是(层数比较深,叶节点上example比较少的)决策树分类器,既然层数比较深所以带有比较多的variance,bagging方法通过两次Random取样降低了variance:第一次是Random地取training example来构建独立的决策树,第二次是在决策树选split point时Random地取一些feature的子集。通过这两次Random就使得每棵决策树Remember了training example的一部分而不是整个的训练集,带来的bias就trade off了深层决策树带来的high variance。随机森林算法的优点是:1、既可以包含binary的feature也可以同时包含标量的feature。2、算法hyperparameters比较少,参数的选取调试对结果的影响不大。3、算法的精度较高。随机森林算法最突出的缺点是由于使用了ensemble,所以算法的速度比较慢。
一般的数据挖掘问题feature engineering十分重要,但是在这个例子里面,给的数据集已经是规范的按像素排列的灰度值,并不需要过多的处理。首先读入数据:
def readCSVFile(file):
rawData=[]
trainFile=open(path+file,'rb')
reader=csv.reader(trainFile)
for line in reader:
rawData.append(line)#42001 lines,the first line is header
rawData.pop(0)#remove header
intData=np.array(rawData).astype(np.int32)
return intData
def loadTrainingData():
intData=readCSVFile("train.csv")
label=intData[:,0]
data=intData[:,1:]
data=np.where(data>0,1,0)#replace positive in feature vector to 1
return data,label
def loadTestData():
intData=readCSVFile("test.csv")
data=np.where(intData>0,1,0)
return data
然后通过scikit-learn的RandomForestClassifier来训练分类器:
def handwritingClassTest():
#load data and normalization
trainData,trainLabel=loadTrainingData()
testData=loadTestData()
testLabel=loadTestResult()
#train the rf classifier
clf=RandomForestClassifier(n_estimators=1000,min_samples_split=5)
clf=clf.fit(trainData,trainLabel)#train 20 objects
m,n=np.shape(testData)
errorCount=0
resultList=[]
for i in range(m):#test 5 objects
classifierResult = clf.predict(testData[i])
resultList.append(classifierResult)
saveResult(resultList)
其中的hyperparameter是通过crossvaildation选出来的,最后输出到csv文件并submit,正确率为96.3%,也不是非常糟糕。
五、第二次尝试:Multi-Layer-Perceptron
由于是图像问题,意识到神经网络应该会有不错的表现,为了防止overfitting,我们先构造一个比较浅层的网络分类器。这里用theano库做一个一层感知机级联一个softmax分类器,为了以后的程序复用性最好把感知机和softmax分类器分别封装成类。首先用pandas库读入DataFrame,并且把42000个example分裂为35000+7000,其中的35000个用于训练,另外的7000个用于validation set(用于early-stop防止overfitting,后面细说)。
def shared_dataset(data_xy,borrow=True):
"""
speed up the calculation by theano,in GPU float computation.
"""
data_x,data_y=data_xy
shared_x=theano.shared(np.asarray(data_x,dtype=theano.config.floatX),borrow=borrow)
shared_y=theano.shared(np.asarray(data_y,dtype=theano.config.floatX),borrow=borrow)
# When storing data on the GPU it has to be stored as floats
# therefore we will store the labels as ``floatX`` as well
# (``shared_y`` does exactly that). But during our computations
# we need them as ints (we use labels as index, and if they are
# floats it doesn't make sense) therefore instead of returning
# `shared_y`` we will have to cast it to int. This little hack
# lets ous get around this issue
return shared_x,T.cast(shared_y,'int32')
def load_data(path):
print '...loading data'
train_df=DataFrame.from_csv(path+'train.csv',index_col=False).fillna(0).astype(int)
test_df=DataFrame.from_csv(path+'test.csv',index_col=False).fillna(0).astype(int)
if debug_mode==False:
train_set=[train_df.values[0:35000,1:]/255.0,train_df.values[0:35000,0]]
valid_set=[train_df.values[35000:,1:]/255.0,train_df.values[35000:,0]]
else:
train_set=[train_df.values[0:3500,1:]/255.0,train_df.values[0:3500,0]]
valid_set=[train_df.values[3500:4000,1:]/255.0,train_df.values[3500:4000,0]]
test_set=test_df.values/255.0
#print train_set[0][:10][:10],'\n',train_set[1][:10],'\n',valid_set[0][-10:][:10],'\n',valid_set[1][-10:],'\n',test_set[0][10:][:10]
test_set_x=theano.shared(np.asarray(test_set,dtype=theano.config.floatX),borrow=True)
valid_set_x,valid_set_y=shared_dataset(valid_set,borrow=True)
train_set_x,train_set_y=shared_dataset(train_set,borrow=True)
rval=[(train_set_x,train_set_y),(valid_set_x,valid_set_y),test_set_x]
return rval
支持符号运算和支持GPU运算加速是theano库的两大亮点。由于要在GPU中计算所以要存为floatX类型,存为shared可以保证只存在变量的一个引用,对于大的数据集十分经济。具体的theano函数参看官网的说明文档,这里不再赘述。
接下来构建一个多类的Logistic Regression(softmax)类:
class LogisticRegression(object):
"""Multi-class Logistic Regression Class"""
def __init__(self,input,n_in,n_out,p_drop_logistic):
"""
:type input: theano.tensor.TensorType
:param input: symbolic variable that describes the input of the architecture(one minibatch)
:type n_in: int
:param n_in: number of input units,data dimension.
:type n_out: int
:param n_out: number of output units,label dimension.
:type p_drop_logistic:float
:param p_drop_logistic: add some noise by dropout by this probability
"""
input=dropout(input,p_drop_logistic)
self.W=theano.shared(value=np.zeros((n_in,n_out),dtype=theano.config.floatX),name='W',borrow=True)
self.b=theano.shared(value=np.zeros((n_out,),dtype=theano.config.floatX),name='b',borrow=True)
self.p_y_given_x=T.nnet.softmax(T.dot(input,self.W)+self.b)
self.y_pred=T.argmax(self.p_y_given_x,axis=1)
self.params=[self.W,self.b]
def negative_log_likelihood(self,y):
"""
The cost function of multi-class logistic regression
:type y:theano.tensor.TensorType
:param y: corresponds to a vector that gives for each example the correct label
"""
# y.shape[0] is (symbolically) the number of rows in y, i.e.,
# number of examples (call it n) in the minibatch
# T.arange(y.shape[0]) is a symbolic vector which will contain
# [0,1,2,... n-1]. T.log(self.p_y_given_x) is a matrix of
# Log-Probabilities (call it LP) with one row per example and
# one column per class. LP[T.arange(y.shape[0]),y] is a vector
# v containing [LP[0,y[0]], LP[1,y[1]], LP[2,y[2]], ...,
# LP[n-1,y[n-1]]] and T.mean(LP[T.arange(y.shape[0]),y]) is
# the mean (across minibatch examples) of the elements in v,
# i.e., the mean log-likelihood across the minibatch.
return -T.mean(T.log(self.p_y_given_x)[T.arange(y.shape[0]),y])
def errors(self,y):
"""
Return a float number of error rate: #(errors in minibatch)/#(total minibatch)
:type y:theano.tensor.TensorType
:param y: corresponds to a vector that gives for each example the correct label
"""
if y.ndim!=self.y_pred.ndim:
raise TypeError('y should have the same shape as self.y_pred')
if y.dtype.startswith('int'):
return T.mean(T.neq(self.y_pred,y))
else:
raise NotImplementedError()
def predict(self):
return self.y_preddef dropout(X,p=0.):
"""
Add some noise to regularize by drop out by probility p
so to prevent overfitting
"""
if p>0:
retain_prob=1-p
srng=RandomStreams()
X*=srng.binomial(X.shape,p=retain_prob,dtype=theano.config.floatX)
X/=retain_prob
return X接下来构造一个由Perceptron构成的HiddenLayer类,其中的Activation function(激励函数)是可以指定的,在2010年以前大范围使用的都是sigmoid function,但是近年来的paper中激励函数更多的是取的tanh和rectify function。我们这里数据量并不大所以暂时不采用求导容易的rectify function。HiddenLayer的代码如下:
class HiddenLayer(object):
def __init__(self,rng,input,n_in,n_out,W=None,b=None,activation=T.tanh,p_drop_perceptron=0.2):
"""
Typical hidden layer of a MLP:units are fully-connected and have
tanh activation function.Weight matrix W is of shape (n_in,n_out),
the bias vector b is of shape(n_out)
:type rng: numpy.random.RandomState
:param rng: a random number generator used to initialize weights
:type input: theano.tensor.dmatrix
:param input: a symbolic tensor of shape (n_examples, n_in)
:type n_in: int
:param n_in: dimensionality of input
:type n_out: int
:param n_out: number of hidden units
:type activation: theano.Op or function
:param activation: Non linearity to be applied in the hidden layer
:type p_drop_perceptron:float
:param p_drop_perceptron: add some noise by dropout by this probability
"""
self.input=dropout(input,p_drop_perceptron)
if W is None:
W_values=np.asarray(rng.uniform(low=-np.sqrt(6./(n_in+n_out)),
high=np.sqrt(6./(n_in+n_out)),size=(n_in,n_out)),
dtype=theano.config.floatX)
if activation==theano.tensor.nnet.sigmoid:
W_values*=4
W=theano.shared(value=W_values,name='W',borrow=True)
if b is None:
b_values=np.zeros((n_out,),dtype=theano.config.floatX)
b=theano.shared(value=b_values,name='b',borrow=True)
self.W=W
self.b=b
lin_output=T.dot(input,self.W)+self.b
self.output=(lin_output if activation is None else activation(lin_output))
self.params=[self.W,self.b]为了使用的方便我们这里把HiddenLayer和LogistRegression类级联的神经网络也封装成一个MLP类,类中的计算全部都是符号运算,MLP类的cost function沿用较后层的softmax分类器的cost function,代码如下:
class MLP(object):
"""Multi-Layer Perceptron Class
A multilayer perceptron is a feedforward artificial neural network model
that has one layer or more of hidden units and nonlinear activations.
Intermediate layers usually have as activation function tanh or the
sigmoid function (defined here by a ``HiddenLayer`` class) while the
top layer is a softamx layer (defined here by a ``LogisticRegression``
class).
"""
def __init__(self,rng,input,n_in,n_hidden,n_out,p_drop_perceptron=0.2,p_drop_logistic=0.2):
"""
:type rng: numpy.random.RandomState
:param rng: a random number generator used to initialize weights
:type input: theano.tensor.TensorType
:param input: symbolic variable that describes the input of the
architecture (one minibatch)
:type n_in: int
:param n_in: number of input units, the dimension of the space in
which the datapoints lie
:type n_hidden: int
:param n_hidden: number of hidden units
:type n_out: int
:param n_out: number of output units, the dimension of the space in
which the labels lie
"""
#We are now dealing with "one hidden layer+ logistic regression" ---Old Network
self.hiddenLayer=HiddenLayer(rng=rng,input=input,n_in=n_in,n_out=n_hidden,activation=T.tanh,p_drop_perceptron=p_drop_perceptron)
self.logRegressionLayer=LogisticRegression(input=self.hiddenLayer.output,n_in=n_hidden,n_out=n_out,p_drop_logistic=p_drop_logistic)
#L1 regularization
self.L1=abs(self.hiddenLayer.W).sum()+abs(self.logRegressionLayer.W).sum()
#L2 regularization
self.L2_sqr=(self.hiddenLayer.W**2).sum()+(self.logRegressionLayer.W**2).sum()
self.negative_log_likelihood=self.logRegressionLayer.negative_log_likelihood
self.errors=self.logRegressionLayer.errors
self.params=self.hiddenLayer.params+self.logRegressionLayer.params
self.predict=self.logRegressionLayer.predict有了几个基本的类以后就可以开始真正的模型的构建过程了,无非就是类的实例化并且调用类中的符号运算计算出的变量来生成theano函数,这里生成的train_model才是我们真正构建的训练模型。而 validate_model是用来利用validation set来early stop防止overfitting的模型,模型构建的代码如下:
def train_old_net():
learning_rate=0.001
L1_reg=0.00
L2_reg=0.0001
n_epochs=100
batch_size=20
n_hidden=500
datasets=load_data(path)
train_set_x,train_set_y=datasets[0]
valid_set_x,valid_set_y=datasets[1]
test_set_x=datasets[2]
#compute number of minibatches
n_train_batches=train_set_x.get_value(borrow=True).shape[0]/batch_size
n_valid_batches=valid_set_x.get_value(borrow=True).shape[0]/batch_size
n_test_batches=test_set_x.get_value(borrow=True).shape[0]/batch_size
print '...building the model'
index=T.lscalar()
x=T.matrix('x')
y=T.ivector('y')
rng=np.random.RandomState(1234567890)
#construct the MLP class
#Attention!!!
#this line to set p_drop_perceptron and p_drop_logistic
#if set no dropout then decrease the early stop threshold
#improvement_threshold on line 292
classifier=MLP(rng=rng,input=x,n_in=28*28,n_hidden=n_hidden,n_out=10,p_drop_perceptron=0,p_drop_logistic=0)
# the cost we minimize during training is the negative log likelihood of
# the model plus the regularization terms (L1 and L2); cost is expressed
# here symbolically
cost=classifier.negative_log_likelihood(y)+L1_reg*classifier.L1+L2_reg*classifier.L2_sqr
#compiling a theano function that computes the mistake rate that
#made by the validate_set on minibatch
validate_model=theano.function(inputs=[index],outputs=classifier.errors(y),
givens={x:valid_set_x[index*batch_size:(index+1)*batch_size],
y:valid_set_y[index*batch_size:(index+1)*batch_size]})
#symbolicly compute the gradient of cost respect to params
#the resulting gradient will be stored in list gparams
gparams=[]
for param in classifier.params:
gparam=T.grad(cost,param)
gparams.append(gparam)
#compiling a Theano function 'train_model' that returns the cost
#but in the same time updates the parameter of the model based on
#the rules defined in 'updates'
train_model=theano.function(inputs=[index],outputs=cost,updates=RMSprop(gparams,classifier.params,learning_rate=0.001),
givens={x:train_set_x[index*batch_size:(index+1)*batch_size],
y:train_set_y[index*batch_size:(index+1)*batch_size]
})#using RMSprop(scaling the gradient based on running average)
#to update the parameters of the model as a list of (variable,update expression) pairs
def RMSprop(gparams,params,learning_rate,rho=0.9,epsilon=1e-6):
"""
param:rho,the fraction we keep the previous gradient contribution
"""
updates=[]
for p,g in zip(params,gparams):
acc=theano.shared(p.get_value()*0.)
acc_new=rho*acc+(1-rho)*g**2
gradient_scaling=T.sqrt(acc_new+epsilon)
g=g/gradient_scaling
updates.append((acc,acc_new))
updates.append((p,p-learning_rate*g))
return updates接下来的就是具体的训练工作,训练的何时停止呢?我们在规定一个阈值的同时采用了early-stop的技术。这是一个十分普遍的技术,下面我们结合代码看一下它是如何工作的:
#early-stopping parameters
patience=10000 #look as this many examples regardless
patience_increase=2 #wait the iter number longer when a new best is found
#improvement_threshold=0.995 # a relative improvement of this much on validation set
# considered as not overfitting
# if have added drop-out noise,we can increase the value
improvement_threshold=0.995
validation_frequency=min(n_train_batches,patience/2)
# every this much interval check on the validation set
# to see if the net is overfitting.
# patience/2 because we want to at least check twice before getting the patience
# include n_train_batches to ensure we at least check on every epoch
best_validation_error_rate=np.inf
epoch=0
done_looping=False
while(epochclassifier.p_drop_perceptron=0
classifier.p_drop_logistic=0
y_x=classifier.predict()
model_predict=theano.function(inputs=[index],outputs=y_x,givens={x:test_set_x[index*batch_size:(index+1)*batch_size]})
digit_preds=Series(np.concatenate([model_predict(i) for i in xrange(n_test_batches)]))
image_ids=Series(np.arange(1,len(digit_preds)+1))
submission=DataFrame([image_ids,digit_preds]).T
submission.columns=['ImageId','Label']
submission.to_csv(path+'submission_sample.csv',index=False)
由于网络比较浅(只有两层),所以运行还是很快的,半小时出结果,提交后错误率97.5%,比随机森林的96%提升了不少。
六、第三次尝试:LeNet5
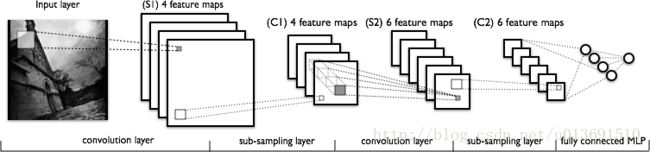
上面的MLP可以看出神经网络确实十分适合用于计算机视觉方面的工作,查阅文献后发现MNIST的识别现在最好的已经可以做到99.5%以上的正确率,看来MLP还有很大的提升空间。提升的空间在哪儿呢,初步判断是layer只有两层导致参数较少underfitting,所以加深网络才是正道。Convolution neural network公认是解决图像识别的最有效的方法之一,我们这里就构建LeCun文章中的LeNet5。LeNet的具体架构如下:
一个卷积层(Convolution layer)和一个池化层(Pooling layer,图中是sub-sampling layer)作为一个LeConvPoolLayer,则LeNet5是两个级联的LeConvPoolLayer级联上一个全连接的Perceptron再级联上一个softmax分类器。与多层感知机的参数是乘法运算的转移weight矩阵不同,卷积层的参数是用于卷积的filter map,这个filter map是学习获得的,初始化时是随机数。所以卷积层的本质是取feature,之所以使用比较小的filter map来取特征是因为这样能够保证在原图像经历了一定的平移时filter出相同的特征。池化层则可以看做是降低分辨率的一步,将临近的几个pixel做平均或者取最大时既保留了主要的feature,又减少了neurons的数目,使得最后全连接感知机的weight参数不至于太多造成计算量大或者overfitting。如此一来,代码实现就比较清楚了:
class LeNetConvPoolLayer(object):
"""
A layer consists of a convolution layer and a pooling layer
"""
def __init__(self,rng,input,filter_shape,image_shape,poolsize=(2,2),p_drop_cov=0.2):
"""
:type rng: numpy.random.RandomState
:param rng: a random number generator used to initialize weights
:type input:theano.tensor.dtensor4
:param input: symbolic image tensor,of shape image_shape
:type filter_shape: tuple or list of length 4
:param filter_shape: (number of filters, num input feature maps,
filter height,filter width)
:type image_shape:tuple or list of length 4
:param image_shape: (batch size,num input feature maps(maps from different channels),
image height, image width)
:type poolsize:tuple or list of length 2
:param poolsize: the downsampling(pooling) factor(#rows,#cols)
"""
assert image_shape[1]==filter_shape[1]
self.input=dropout(input,p_drop_cov)
#there are "num input feature maps(channels) * filter height * filter width"
#input to each hidden unit
fan_in=np.prod(filter_shape[1:])
#each unit in the lower layer receives a gradient from:
#"num output feature maps * filter height * filter width"
# / pooling size
fan_out=(filter_shape[0]*np.prod(filter_shape[2:])/np.prod(poolsize))
#initialize weights with random weights
W_bound=np.sqrt(6./(fan_in+fan_out))
self.W=theano.shared(np.asarray(rng.uniform(
low=-W_bound,high=W_bound,size=filter_shape),
dtype=theano.config.floatX),borrow=True)
#the bias is a 1D tensor-- one bias per output feature map
b_values=np.zeros((filter_shape[0],),dtype=theano.config.floatX)
self.b=theano.shared(value=b_values,borrow=True)
#convolve input feature maps with filters
conv_out=conv.conv2d(input=input,filters=self.W,filter_shape=filter_shape,image_shape=image_shape)
#pooling each feature map individually,using maxpooling
pooled_out=downsample.max_pool_2d(input=conv_out,ds=poolsize,ignore_border=True)
#add the bias term.Since the bias is a vector (1D array),we first
#reshape it to a tensor of shape(1,n_filters,1,1).Each bias will thus
#be broadcasted across mini-batches and feature map width& height
self.output=T.tanh(pooled_out+self.b.dimshuffle('x',0,'x','x'))
#store parameters of this layer
self.params=[self.W,self.b]
def return_output():
return self.output这里需要注意的一点是在卷积之后池化之前我们需要在feature map上加上一个bias量(上述类中用b表示),feature map是一个4维的tensor,而bias是一个一维的tensor,这里就需要用到tensor的广播机制,这一点上theano库算是充分发挥了python的优势,具体的用法可以参加theano库dimshuffle函数的说明。有了LeConvPoolLayer之后构建实际的模型就按照LeNet5的图示级联即可:
def train_lenet():
learning_rate=0.001
#if not using RMSprop learn_rate=0.1
#if using RMSprop learn_rate=0.001
nkerns=[20,50]
batch_size=500
"""
:type nkerns:list of ints
:param nkerns: nkerns[0] is the number of feature maps after 1 LeCovPoollayer
nkerns[1] is the number of feature maps after 2 LeCovPoolllayer
"""
rng=np.random.RandomState(1234567890)
datasets=load_data(path)
train_set_x,train_set_y=datasets[0]
valid_set_x,valid_set_y=datasets[1]
test_set_x=datasets[2]
#compute number of minibatches
n_train_batches=train_set_x.get_value(borrow=True).shape[0]
n_valid_batches=valid_set_x.get_value(borrow=True).shape[0]
n_test_batches=test_set_x.get_value(borrow=True).shape[0]
n_train_batches/=batch_size
n_valid_batches/=batch_size
n_test_batches/=batch_size
#allocat symbolic variables for the data
index=T.lscalar() #index to minibatch
x=T.matrix('x') #image
y=T.ivector('y') #labels
ishape=(28,28) #MNIST image size
p_drop_cov=0.
p_drop_perceptron=0.
p_drop_logistic=0. #probablities of drop-out to prevent overfitting
#########################
# Building actual model #
#########################
print '...building the model'
#reshape matrix of images of shape (batch_size,28,28)
#to a 4D tensor, compatible with our LeNetConvPoolLayer
layer0_input=x.reshape((batch_size,1,28,28)) #batch_size* 1 channel* (28*28)size
#Construct the first convolutional pooling layer:
#filtering reduces the image size to (28-5+1,28-5+1)=(24,24)
#maxpooling reduces this further to (24/2,24/2)=(12,12)
#4D output tensor is thus of shape (batch_size,nkerns[0],12,12)
layer0=LeNetConvPoolLayer(rng,input=layer0_input,
image_shape=(batch_size,1,28,28),
filter_shape=(nkerns[0],1,5,5),poolsize=(2,2),p_drop_cov=p_drop_cov)
# Construct the second convolutional pooling layer:
# filtering reduces the image size to (12-5+1,12-5+1)=(8,8)
# maxpooling reduces this further to (8/2,8/2) = (4,4)
# 4D output tensor is thus of shape (batch_size,nkerns[1],4,4)
layer1 = LeNetConvPoolLayer(rng, input=layer0.output,
image_shape=(batch_size, nkerns[0], 12, 12),
filter_shape=(nkerns[1], nkerns[0], 5, 5), poolsize=(2, 2),p_drop_cov=p_drop_cov)
#the HiddenLayer being fully-connected,it operates on 2D matrices shape
#(batch_size,num_pixels)
#This will generate a matrix of shape (batch_size,nkerns[1]*4*4)=(500,800)
layer2_input=layer1.output.flatten(2)
#construct a fully-connected perceptron layer
layer2=HiddenLayer(rng,input=layer2_input,n_in=nkerns[1]*4*4,n_out=500,activation=T.tanh,p_drop_perceptron=p_drop_perceptron)
#classify the values of the fully connected softmax layer
layer3=LogisticRegression(input=layer2.output,n_in=500,n_out=10,p_drop_logistic=p_drop_logistic)
#the cost we minimize during training
cost=layer3.negative_log_likelihood(y)
#create a function to compute the error rate on validation set
validate_model=theano.function([index],layer3.errors(y),
givens={x:valid_set_x[index*batch_size:(index+1)*batch_size],
y:valid_set_y[index*batch_size:(index+1)*batch_size]})
#create a list of gradients for all model parameters
params=layer3.params+layer2.params+layer1.params+layer0.params
grads=T.grad(cost,params)
#using RMSprop(scaling the gradient based on running average)
#to update the parameters of the model as a list of (variable,update expression) pairs
def RMSprop(gparams,params,learning_rate,rho=0.9,epsilon=1e-6):
"""
param:rho,the fraction we keep the previous gradient contribution
"""
updates=[]
for p,g in zip(params,gparams):
acc=theano.shared(p.get_value()*0.)
acc_new=rho*acc+(1-rho)*g**2
gradient_scaling=T.sqrt(acc_new+epsilon)
g=g/gradient_scaling
updates.append((acc,acc_new))
updates.append((p,p-learning_rate*g))
return updates
#iterate to get the optimal solution using minibatch SGD
#updates=[]
#for param,grad in zip(params,grads):
#updates.append((param,param-learning_rate*grad))
train_model=theano.function([index],cost,updates=RMSprop(grads,params,learning_rate),
givens={ x:train_set_x[index* batch_size:(index+1)*batch_size],
y:train_set_y[index* batch_size:(index+1)*batch_size]
})这里同样加入了drop-out防止overfitting,加入了RMSprop加速SGD的迭代收敛速度。训练的过程与MLP相仿,也采用early-stop防止overfitting,这里不再赘述。由于LetNet5是一个包含5层的网络,参数比较多,所以训练的速度比MLP要慢的多,可以采用theano库的GPU运算配置加速5倍左右。最后在我的laptop上大概2小时出结果,从log中看出大概30个epoch时就基本收敛了,最后Kaggle上提交正确率99.1%,排名在28/554,前5%的名次。之所以没有达到99.5%的理论值可能是由于training example不够多,可以考虑对training example做左(右)旋5度来获得更多的training example或许会进一步提高正确率,由于手头事情多我没有做。但是个人觉得上下或者左右的平移并不会带来正确率的提升,因为在平移变化下取得的卷积特征是不变的。
七、本文所需的一些背景
1、机器学习基础知识:Adrew Ng的Coursera课程,目前已经结课但是资料可以看。里面有一些编程左右,我自己做了一份提交验证过的答案。
2、机器学习基础知识:Adrew Ng的UFLDL网页,我自己也做了一份答案。
3、theano教程,我在github上fork了一个branch,大家有兴趣可以看看。
4、我做的本文的项目python代码。