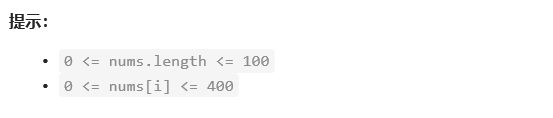动态规划:力扣198. 打家劫舍,以及这系列题的解题方法和思路(包括打家劫舍 II、打家劫舍 III)
力扣198打家劫舍
1、题目描述:
2、题解:
动态规划:
1、状态定义;
2、状态转移方程;
3、初始化;base case
4、输出;
5、思考状态压缩。
可以用递归去求,但是会存在重叠子问题,加个备忘录可以解决重复问题。
1)先用递归+备忘录来求:
一个位置可以抢也可以不抢,如果抢了,那么下一个位置不能抢;不过不抢则下一个位置可以抢。当走到最后一个房间时 ,就不可以抢了,也就是能抢到的钱为0.
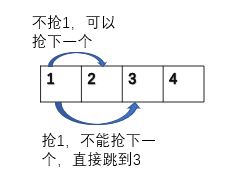
写出递归函数:
class Solution:
def rob(self, nums: List[int]) -> int:
def dp (nums,start):
if start >= len(nums):
return 0
#(不抢,抢)
res = max(dp(nums,start + 1),dp(nums,start + 2) + nums[start])
return res
return dp(nums,0)这个由于存在重复子问题,可能会超时,我们加个备忘录:
class Solution:
def rob(self, nums: List[int]) -> int:
def dp (nums,start):
if start >= len(nums):
return 0
if memo[start] != -1 :
return memo[start]
#(不抢,抢)
memo[start] = max(dp(nums,start + 1),dp(nums,start + 2) + nums[start])
return memo[start]
#初始化备忘录
memo = [-1] * len(nums)
#从0间房子开始抢
return dp(nums,0)2}动态规划:
状态定义:
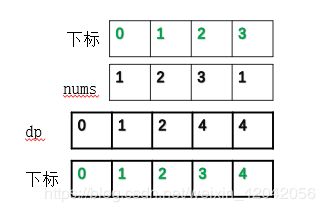
dp[i]为偷前i个房间的最大金额
状态转移方程:
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i-1])
#解释:dp[i]的值为下面两种情况的最大值:
#不偷nums[i-1]和偷nums[i-1],分别对应dp[i - 1], dp[i - 2] + nums[i-1]
#dp比nums的长度大1base case:
定义初始时dp都为0,i=0时代表前0个房子,dp[0] = 0;i=1时为前1个房子的最大金额,应该为nums[0]class Solution:
def rob(self, nums: List[int]) -> int:
#动态规划
n = len(nums)
if n == 0:
return 0
dp = [0] * (n + 1)
dp[0] = 0
dp[1] = nums[0]
for i in range(2,n + 1):
dp[i] = max(dp[i-1],dp[i-2] + nums[i-1])
return dp[n]当然我们也可以这样:
class Solution:
def rob(self, nums: List[int]) -> int:
#动态规划
n = len(nums)
if n == 0:
return 0
if n == 1:
return nums[0]
dp = [0] * n
dp[0] = nums[0] #当有一个值时,偷它,就是最大金额
dp[1] = max(nums[0],nums[1])#当有两个值时,偷其中最大的
for i in range(2,n):
dp[i] = max(dp[i-1],dp[i-2] + nums[i])
return dp[n-1]空间优化:
class Solution:
def rob(self, nums: List[int]) -> int:
#动态规划
n = len(nums)
if n == 0:
return 0
pre = 0
cur = 0
for num in nums:
temp = cur
cur = max(cur,pre + num)
pre = temp
return cur3、复杂度分析:
空间未优化前:
时间复杂度和空间复杂度都是O(N)
空间优化后:
时间复杂度是O(N)
空间复杂度是O(1)
213. 打家劫舍 II
1、题目描述:
2、题解:
此题和上题的思路差不多,只不过是环形的,也就是说第一个房间和最后一个房间只能有一个被偷:
第一个房间被偷为my_rob(nums[:-1]),最后一个房间被偷ya_rob(nums[1:])。
class Solution:
def rob(self, nums: List[int]) -> int:
def my_rob(nums):
pre,cur = 0,0
for num in nums:
cur ,pre = max(cur,pre + num),cur
return cur
n = len(nums)
if n == 0:
return 0
if n == 1:
return nums[0]
return max(my_rob(nums[:-1]),my_rob(nums[1:]))337. 打家劫舍 III
1、题目描述:
2、题解:
”抢劫“的对象变成了二叉树,我们在递归时,要加一个备忘录
class Solution:
def rob(self, root: TreeNode) -> int:
def my_rob(root):
if not root:
return 0
#如果备忘录里,直接返回备忘录里的值
if root in hashmap:
return hashmap[root]
#抢,然后去下下家
rob_it = root.val + ((my_rob(root.left.left) + my_rob(root.left.right)) if root.left != None else 0) + \
((my_rob(root.right.left) + my_rob(root.right.right)) if root.right != None else 0)
#不抢,然后去下家
not_rob = my_rob(root.left) + my_rob(root.right)
hashmap[root] = max(rob_it,not_rob)
return hashmap[root]
#备忘录
hashmap = {}
return my_rob(root)或者,
我们换一种办法来定义此问题:
每个节点可选择偷或者不偷两种状态,根据题目意思,相连节点不能一起偷
当前节点选择偷时,那么两个孩子节点就不能选择偷了
当前节点选择不偷时,两个孩子节点只需要拿最多的钱出来就行(两个孩子节点偷不偷没关系)
我们使用一个大小为 2 的数组来表示 res = []*2 0 代表不偷,1 代表偷
任何一个节点能偷到的最大钱的状态可以定义为:
当前节点选择不偷:当前节点能偷到的最大钱数 = 左孩子能偷到的钱 + 右孩子能偷到的钱
当前节点选择偷:当前节点能偷到的最大钱数 = 左孩子选择自己不偷时能得到的钱 + 右孩子选择不偷时能得到的钱 + 当前节点的钱数
root[0] = max(my_rob(root.left)[0],my_rob(root.left)[1]) + max(my_rob(root.right)[0],my_rob(root.right)[1])
root[1] = root.val + my_rob(root.left)[0] + my_rob(root.right)[0] def my_rob(root):
if not root:
return [0,0]
left = my_rob(root.left)
right = my_rob(root.right)
#不抢root,下家可抢可不抢,取决于收益大小
not_rob = max(left[0],left[1]) + max(right[0],right[1])
#抢root,下家就不能抢了
rob_it = root.val + left[0] + right[0]
return [not_rob,rob_it]
res = my_rob(root)
return max(res[0],res[1])