二叉堆详解实现优先级队列
开篇
今天说一种在排序方面有很大作用的数据结构。我们都知道在排序方面最快的算法应该是快速排序,时间复杂度为O(nlogn),但这个算法不稳定,如果数组本身就有序的话会浪费很多时间。还有一种无论在空间和时间角度都很稳定且快速的排序方法——堆排序。堆排序利用的数据结构就是一个优先队列。所以这次我们就详述一下用二叉堆来实现一个优先队列。
二叉堆概述
首先我们说一下二叉堆和二叉树的关系。为什么总有人把二叉堆画出二叉树呢?
因为二叉堆其实就是一种特殊的二叉树(完全二叉树),只不过存储在数组里。(所以我们的排序过程应该是在数组中原地进行的)。一般的链表二叉树,我们操作节点的指针,而在数组里,我们用数组的索引当作指针即可:
//父节点的指针
int parent(int root)
{
return root/2;
}
//左孩子的索引
int left(int root)
{
return root*2;
}
//右孩子的索引
int parent(int root)
{
return root*2+1;
}我们初始化根节点的索引为1,所以左孩子应该是2root,右孩子是2root+1.
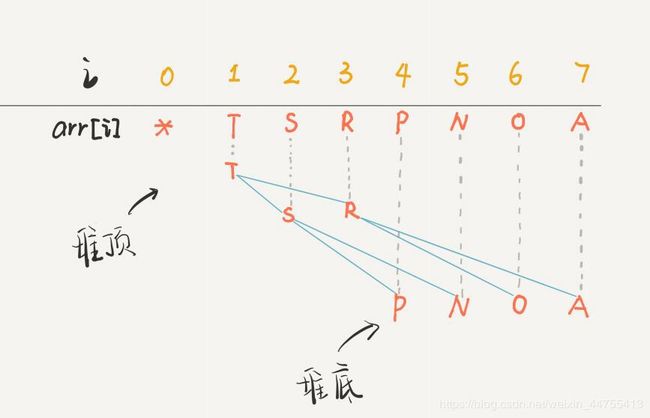
二叉堆还分为最大堆和最小堆,最大堆的性质是:每个结点都大于等于它的子节点。类似的,最小堆的性质是:每个节点都小于等于它的子节点。
两种堆核心思路是一样的,本文以最大堆为例讲解。
对于一个最大堆,根据其性质,显然堆顶也就是arr[1]一定是所有元素中最大的元素。
优先队列概述
优先队列的最主要的特点就是:内部有序。
而主要功能就是在我们插入或删除任何一个节点,元素都会在堆中自动排序,这底层原理就是二叉堆的操作。
优先级队列有主要两个API,分别是insert插入一个元素和delMax删除最大元素(如果底层是一个最小堆,那么就是delMin).
下面我们就来实现一个简化的优先级队列,先看下代码框架,我们以节点数据类型为int举例:
class MaxPQ{
private:
int pq[];//存储元素的数组
int N = 0;//当前优先队列中的元素个数
//上浮第k个元素以维护最大堆的性质
void swim(int k){.....}
//下沉第k个元素以维护最大堆的性质
void sink(int k){....}
//交换数组的两个元素
void exch(int i,int j)
{
int temp = pq[i];
pq[i] = pq[j];
pq[j] = temp;
}
//pq[i]是否小于pq[j]
bool less(int i,int j)
{
return pq[i] < pq[j];
}
public:
MaxPQ(int cap)
{
//索引0不用,所有多分配一个内存空间
pq = new int[cap+1];
}
//返回当前队列中最大的元素
int max()
{
return pq[1];//最大堆的根节点最大
}
//插入元素
void insert(int e){.....}
//删除并返回当前队列中最大元素
int delMax(){.....} 空出来的方法就是二叉堆实现优先级队列的精髓所在,下面我们来具体实现一下这四个位置。
实现swim和sink
为什么要上浮swim和下沉?为了堆结构。我们要讲的是最大堆,每个结点都比它的两个子结点大,但是在插入元素和删除元素时,难免会破坏堆的性质,这就需要通过这两个操作来恢复堆的性质了,它们可以在我们完成插入和删除后自动对堆进行调整,从而使堆仍然具有最大堆的性质。
破坏最大堆性质有两种情况:
1.如果某个结点A比它的子节点(中的一个)小,那么A就不配做父节点,应该处于下面,找下面那个更大的上来做父节点,这个操作就是对A结点的下沉操作。
2.如果某个结点大于它的父节点,那么这个结点就不应该做子节点,应与其父节点交换,自己去做父节点,这个操作叫做上浮。
我们可以看出上浮和下沉两个操作是对应的,上浮的过程必然伴随着下沉,下沉的过程也必然伴随着上浮,只是二者操作的对象不同。
当然啦,如果一个很大的结点A在堆的最下面,那么A一定会上浮好多次,所以这里我们应该写一个while循环来持续上浮,直到A的父节点比它大。
这里相信很多朋友都会有一个疑问,既然这两个操作是互逆的,我们为什么要写两个呢?写一个不就全都解决了吗?没错,这两个操作时互逆的没错,我们也说了上浮伴随着下沉,下沉伴随着上浮。但是那只是在堆中某个结点的操作,但是请注意我们现在是一个最大堆,我们的操作只会在堆顶和堆底发生,所以我们应该让堆顶元素下沉,堆底元素上浮,从而塑造出一个最大堆。之所以会在堆顶和堆底操作,具体原因后面会说明。
上浮代码的实现
void swim(int k)
{
//如果浮到了堆顶,就不能再上浮了
while(k>1&&less(parent(k),k))
{
//如果第k个元素比上层大
//将k换上去
exch(parent(k),k);
k = parent(k);下沉代码的实现
下沉稍微复杂一点,因为上浮某个结点A,只需要A和其父节点比较大小即可,而下沉需要和左右两个孩子结点比较大小,找一个最大的与父节点交换,如果父节点就是最大的,就不用交换了。
void sink(int k)
{
//如果沉到了堆底,就沉不下去了
while(left(k)<=N)
{
//先假设左边结点较大
int older=left(k);
//如果右边结点存在,比一下大小
if(right(k)<=N && less(older,right(k)))
older = right(k);
//再比较一下父节点和两个孩子结点,如果父节点大就不用下沉了
if(less(older,k))
break;
//否则,不符合最大堆的结构,下沉k结点
exch(k,older);
k = older;
}
}二叉堆的主要操作说完了,我们已经塑造好了一个最大堆,下面就是利用这个二叉堆来实现优先级队列了。
实现delMax和insert
insert方法先把要插入的元素添加到堆底的最后,然后让其上浮到正确位置
这就是我们所说的只在堆顶和堆底操作的原因,我们总是把元素先放在堆底,如果该元素大于堆顶的元素,我们就将其于堆顶交换,然后再将插入位置的元素(即原堆顶元素)上浮至其应该的位置。如果插入的元素小于堆顶元素,直接上浮就完事了。
void insert(int e)
{
N++;
//先把新元素加到最后
pq[N] = e;
//然后让它上浮到正确的位置
swim(N);
}delMax方法先把对顶元素A和堆底最后的元素B对调,然后删除A,最后让B下沉到正确的位置。
int delMax()
{
//最大堆的堆顶就是最大元素
int max = pq[1];//索引从1开始,我们规定好的
//把这个最大元素换到最后删除
exch(1,N);
pq[N] = NULL;
N--;
//让pq[1]下沉到正确的位置
sink(1);
return max;至此一个优先级队列就完成了,插入和删除元素的时间复杂度为O(logK),K为当前二叉堆中的元素总数,我们大多数的时间花费在sink和swim操作上,不管上浮还是下沉,最多也就操作树的高度次,也就是log级别的。
总结
OK,二叉堆和优先级队列我们就说完了,这是一个非常常用且有效的数据结构,因为它可以存储在数组中,通过索引直接访问,所以十分方便。
最主要的仍然是我们开头就说明的,它可以自动维护堆的性质,所以我们可以肆意地插入和删除,最大堆和最小堆的性质都不会改变。