编码和可靠性编码

编码的主要目的

因为电路是二进制的,而平时使用的一般都是十进制,所以需要一种快捷可靠的编码作为转换以更简明的方式传达信息.同时,由于数据传输中不可避免地存在错误(对于二进制是0/1翻转),编码的校验也十分重要.

BCD码:8421,2421,余3

8421

用4位二进制码表示一位十进制字符的一种有权码，4位二进制码从高位 至低位的权依次为为8、4、2、1。每一位DEC强制占4位HEX.比如9的8421码就是(1001)
需要注意的是,8421码虽然表达方便,但有冗余空间即存在无关解,若产生错误难以修正.8421的冗余位有1010～1111六种.
另外,十进制数字符0～9的8421码与相应ASCII码的低四位相同，有利于简化输入输出过程中BCD码与字符代码的转换。

2421

2421码为了消除8421中的冗余项,最高项权值变成2.但由于不具备单值性(1000=0010=2),所以不出现0101～1010.(至于为什么,参照最下面2421的性质.)
注意,有一条重要的性质决定在有多重取值的时候用哪一种:数和其对9的补应为互为反码.这个在进行减法运算时十分有用.

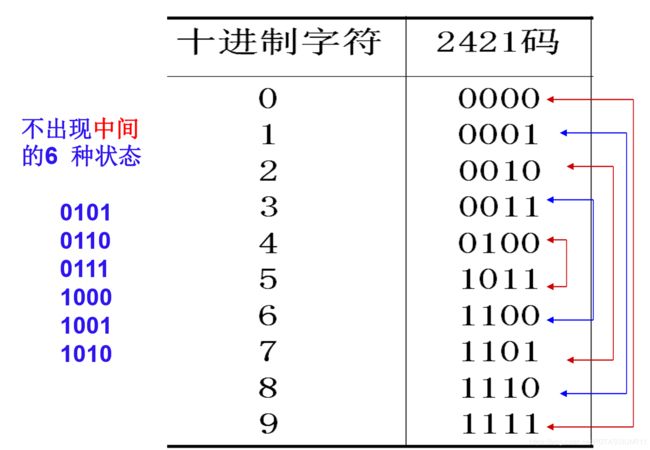
0-9的2421码

余3码

• 在8421码基础上通过加3(0011)形成的一种无权码。也就是说不会小于3.
• 余3码中不允许出现0000、0001、0010、1101、1110、1111六种组合；
• 是一种对9的自补代码,跟2421一样.

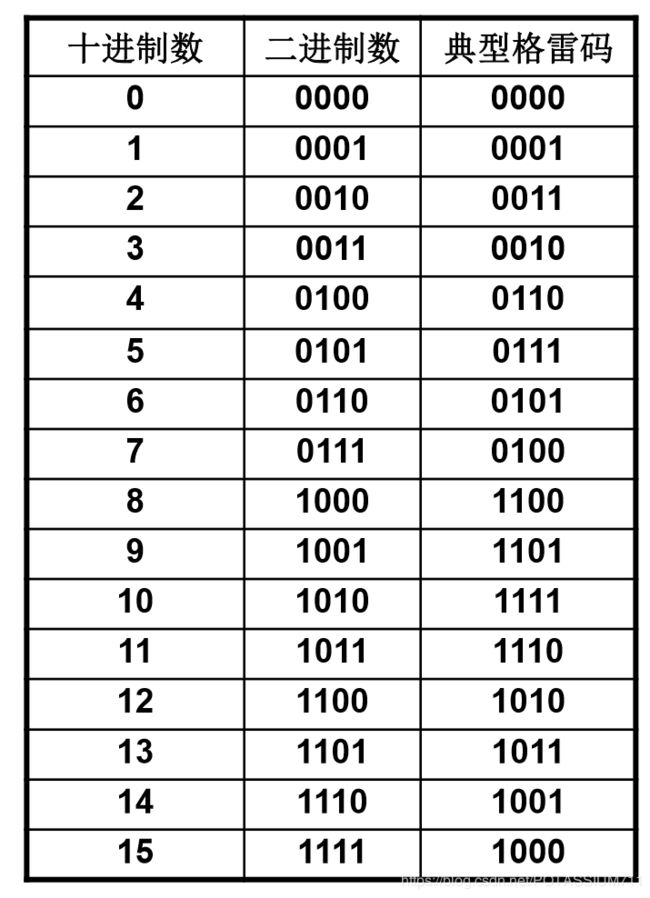
下面是三种编码方式的码表.

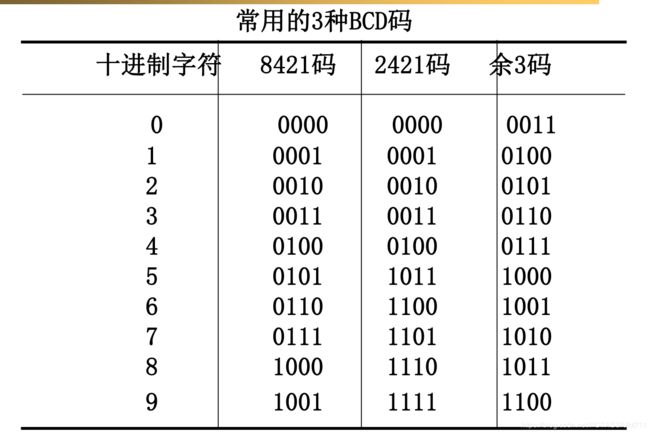
Ref: http://www.elecfans.com/dianzichangshi/2009101396359.html

格雷码:相邻码

格雷码最大的特点是两个十进制数的编码表示是[相邻]的(具体定义见之前的文章),也就是有且只有某一位的数字不同.但从严格意义上来说,格雷码的特点不在于此.
格雷码的生成依赖于异或运算.即:如下真值表:

Column 1	Column 2
0,0	0
0,1	1
1,0	1
1,1	0

异或运算的本质就是对于相同的两个输入输出0,否则为1.
也可理解为二进制在Single digit上的加法运算.
而格雷码的生成按照如下规则:
对于一个十进制数的二进制,

• 最高位不变;
• 剩下每一位的格雷编码为该位和上一位的异或.

用下面一张图可以辅助理解:

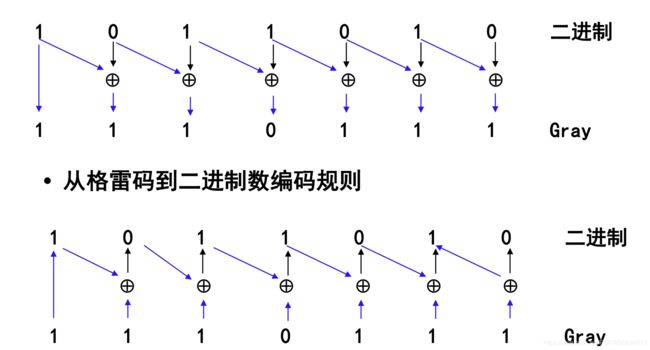
而解码则是完全一样的过程.
因为由异或的规则可知a异或b异或b=a.

格雷码的电路实现.

借助异或门,格雷码的编码和解码都很简单,而且可以复用.

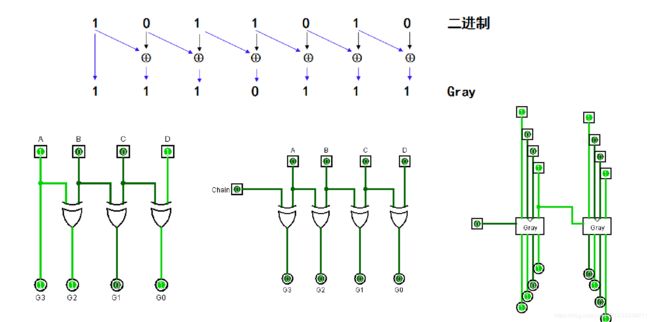
注意如果是要求可扩展的格雷码编码封装元件,最高的一个异或门要设扩展位.

格雷码的意义

格雷码任意两个相邻数仅有一位不同,为了防止代码形成或变换过程中因时延产生的错误.

---

可靠性编码

为什么需要可靠性编码?

• 自然界存在很多干扰
• 二进制数据在被处理、传输、存储的过程中受干扰易发生错误
• 数据是被处理、传输和存储的直接对象;
• 当直接对象出现错误时若不能检测，高层检测将会付出更大的代 价！(将问题解决在基层)
• 编码与数据在同一层,可以提供参考对象,便于检错与纠错。

校验的基本原理

一个有可靠性的编码在传输过程中应包括k位有效信息和r位校验信息.发送方对有效信息编码后传输,接收方用这两部分信息进行校验即可确定传输数据的可信度,或者进行纠错(某些可靠性编码的确可以这么干)

码距

码距就是同一编码中，任意两个合法编码之间不同二进数位数的最小值.比如0001和0000,只有一位不同,码距为1所以当最后一位发生错误时(可靠性永远考虑最坏的情况)无法识别.再如 0000、0011、0101、0110、1001、1010、1100、1111等编码码距为2。任何一位发生改变，如0000变成1000就从有效编码变 成了无效编码，容易检测到这种错误。
简而言之,码距代表了该编码方案检错和纠错的能力.
码距可以通过添加冗余项来增大.但这也会造成传输效率的大幅下降.这一点需要仔细权衡.

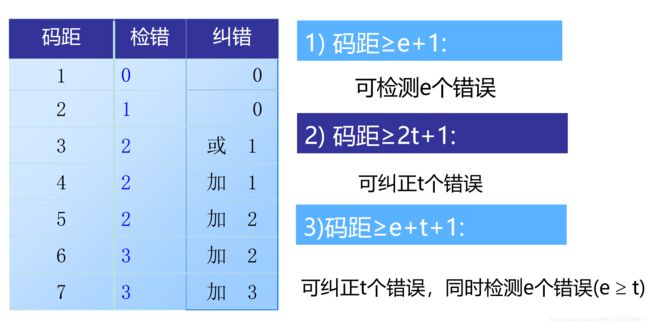
码距与检错或纠错能力的关系

奇偶校验

奇偶校验是一种常用的简单的可靠性编码方案,有k位有效信息和1位校验信息.

编码方案

根据有效信息计算校验信息位，使校验码（数据＋1位 校验信息）中1的个数满足奇/偶校验的要求.比如:
有效信息1000->奇校验=1000 0/偶校验=1000 1
用逻辑表达式来表述:
由异或的性质,奇数个1异或得到1,偶数个是0.那么:
对于奇数校验:式为:所有项异或并取反
对于偶数校验,式为:所有项异或.

校验方案:

检查位数是否与声称的编码方案一致.依然是对所有位(包含校验位)异或,如果为1,则应为奇数校验;如果为0,则应为偶数校验.

性能分析

• 编码与检错简单
• 编码效率高
• 不能检测偶数位错误, 无错结论不可靠，是一种错误检测码 (也就是说当出现偶数位错误时无法检测)
• 不能定位错误，因此不具备纠错能力

对于二进制编码来说,定位到错误就可以纠错.
一般在同步传输方式中常采用奇校验，异步传输方式中常采用偶校验.

---

此外还有汉明码和CRC校验,具体见下面的参考链接,在此不做赘述.
https://www.wikiwand.com/zh-hans/汉明码
https://baike.baidu.com/item/CRC校验