【软件分析学习笔记】2:数据流分析及示例,半格和偏序
1 简述数据流分析
数据流(dataflow)分析将程序看成数据和数据的流动转移,而将转移的控制条件忽略掉,只关注数据在转移过程中的变化。
例如,对于上一节的停机问题的反例程序:
void Evil() {
if(Halt(Evil)==False)
return;
else
while(True);
}
其中的if-else就是控制条件,将它忽略掉,抽象成一对非确定选择(即在这里程序随机选择一条路走)向左走 ⊓ \sqcap ⊓向右走:
void Evil() {
向左走 return;
向右走 while(True);
}
即使没有了if-else,停机问题的反例程序还可以单纯用循环给出:
void Evil() {
while(Halt(Evil))
;
}
这里的循环条件也属于控制条件,将它也抽象成非确定选择:
void Evil() {
AGAIN:
向左走 goto AGAIN;
向右走 return;
}
像这样将原始程序中的控制条件都抽象成非确定选择,忽略程序的条件判断,认为所有分支都可能到达,就得到了抽象程序。原始程序只有一条执行路径,抽象程序上有多条执行路径。原始程序的执行路径一定包含在抽象程序的执行路径中,所以对原始程序的问题判定可以转换成对抽象程序的判定。
如对停机问题,原始程序上要求存在自然数n,使程序执行路径长小于n。而对于抽象程序,是存在自然数n,使程序所有路径长度都小于n。
注意,抽象程序上的判定问题,得到的是上/下近似的解而不是确定解。如对停机问题而言,实际上就是将抽象程序绘制成流程图,如果流程图中没有环,那么可以说原始程序一定停机;如果流程图中有环,那么要返回[不知道],因为不存在自然数n使得所有路径长度都小于n(抽象程序的流程图中已经没有条件控制了,环路长度就是无穷)。
2 例:符号分析
符号判定问题的数据流分析。
2.1 简述
回顾笔记1中第6部分的符号判定问题。对于给定的程序,去掉分支判断和条件循环之后,得到的抽象程序会有很多分支。使用抽象符号域上作运算的方法,引入[不知道],在 n n n个不同的分支上分别得到结果 v 1 , v 2 , . . . , v n ∈ { 正 , 负 , 零 , 不 知 道 } v_1,v_2,...,v_n \in \{正,负,零,不知道\} v1,v2,...,vn∈{正,负,零,不知道},最终判定的输出就是:
⊓ ( v 1 , v 2 , . . . , v n ) \sqcap(v_1,v_2,...,v_n) ⊓(v1,v2,...,vn)
如果 v i v_i vi和 v j v_j vj一样,非确定选择 ⊓ \sqcap ⊓合并的结果就是 v i v_i vi,否则结果就是[不知道]。
为了减少计算量,不必在每条路径结尾做合并,可以在控制流结束汇合的地方提前合并,再将合并结果向下运算,如对于:
xxx
if(xxx)
xxx
else
xxx
while(xxx)
xxx
xxx
xxx
...
那么只要在while循环结束的地方(即是控制流汇合的地方)提前合并即可。
2.2 算法过程
3 例:活跃变量分析
活跃变量判定问题的数据流分析。
3.1 简述
给出程序中的变量 x x x和程序点 p p p,如果 x x x会在从 p p p出发的某条路径上使用,那么 x x x对于 p p p点而言就是活跃变量,否则就不是。活跃变量的分析可以用来做寄存器的换出,对于不活跃的变量没必要再占用寄存器资源。
3.2 算法过程
逆向计算路径上的活跃变量,见这篇文章。
4 半格和偏序
4.1 半格(Semilattice)
半格是二元组 ( S , ⊓ ) (S,\sqcap) (S,⊓),其中 S S S是一个集合, ⊓ \sqcap ⊓是一个交汇运算(也就是集合中若干元素经过这个运算会聚合成一个)。要求对 S S S中的任意元素,在运算 ⊓ \sqcap ⊓上是幂等、交换、结合的,而且 S S S中要存在一个最大元(或者叫顶元素) T T T使得任意 x ∈ S x\in S x∈S有 x ⊓ T = x x \sqcap T = x x⊓T=x。
例如,正整数集合上的"求最小公倍数"的运算就是一个半格,其中最大元 T = 1 T=1 T=1。
半格的笛卡尔积还是半格:
( S 1 , ⊓ 1 ) × ( S 2 , ⊓ 2 ) = ( S 1 × S 2 , ⊓ 1 × ⊓ 2 ) (S_1, \sqcap_1) \times (S_2, \sqcap_2) = (S_1 \times S_2, \sqcap_1 \times \sqcap_2) (S1,⊓1)×(S2,⊓2)=(S1×S2,⊓1×⊓2)
4.2 偏序(Partial Order)
偏序是二元组 ( S , ⊑ ) (S,\sqsubseteq) (S,⊑),其中 S S S是一个集合, ⊑ \sqsubseteq ⊑是一个二元关系,要求这个二元关系 ⊑ \sqsubseteq ⊑是自反、传递、反对称的。
例如,实数集合上的小于等于关系就是一个偏序关系。
4.3 半格和偏序的关系
每个半格 ( S , ⊓ ) (S,\sqcap) (S,⊓)都定义了同一集合 S S S上的一个偏序关系 ( S , ⊑ ) (S,\sqsubseteq) (S,⊑),具体是:
x ⊑ y 当 且 仅 当 x ⊓ y = x x \sqsubseteq y 当且仅当 x \sqcap y = x x⊑y当且仅当x⊓y=x
例如,正整数集合上的"求最小公倍数运算"是半格,而"整除关系"是对应的偏序。
又如,任意集合和"交集操作"组成了一个半格,顶元素是全集,而"子集关系"是对应的偏序。
又如,任意集合和"并集操作"组成了一个半格,顶元素是空集,而"超集关系"是对应的偏序。
4.4 半格的例子——抽象符号域的交汇操作
对于2的符号分析,在2.2中可以看到扩展的抽象符号域是:
{ 正 , 负 , 零 , 未 知 , T } \{正,负,零,未知,T\} {正,负,零,未知,T}
那么这个集合上的交汇操作就是一个半格了,其中最大元就是 T T T,而从:
未 知 ⊓ 正 = 未 知 正 ⊓ T = 正 . . . 未知 \sqcap 正 = 未知 \\ 正 \sqcap T = 正 \\ ... 未知⊓正=未知正⊓T=正...
这些交汇操作规则可以导出这个半格对应的偏序关系:
未 知 ⊑ 正 正 ⊑ T . . . 未知 \sqsubseteq 正 \\ 正 \sqsubseteq T \\ ... 未知⊑正正⊑T...
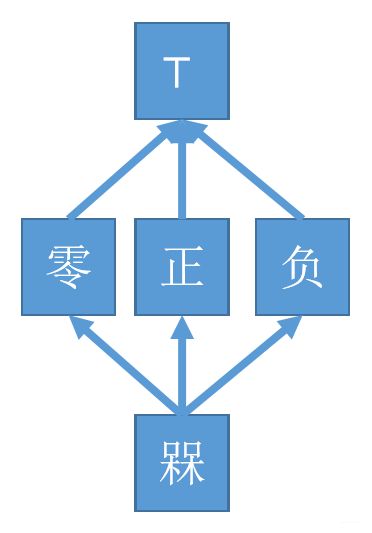
可以将这些偏序关系整合成偏序图:
可以看到从下往上画偏序图的话,偏序关系对应的半格的顶元素(最大元)就是在最顶上的。
4.5 半格的高度
半格的高度是对应偏序关系的偏序图中任意两个结点的最大距离+1,例如4.4抽象符号域的交汇操作的半格,高度就是3。
又如,集合和交集/并集操作组成的半格,高度是集合大小+1。
又如,活跃变量分析中,半格高度为变量总数+1。
4.6 单调(递增)函数
单调函数是定义在偏序关系上的。给定偏序关系 ( S , ⊑ ) (S,\sqsubseteq) (S,⊑),称一个定义在 S S S上的函数是单调递增的,当且仅当对任意 x , y ∈ S x,y \in S x,y∈S有:
x ⊑ y ⇒ f ( x ) ⊑ f ( y ) x \sqsubseteq y \Rightarrow f(x) \sqsubseteq f(y) x⊑y⇒f(x)⊑f(y)
例如,对2符号分析中的加减乘除操作(固定一个参数)都是单调函数。
和3活跃变量分析有关的是, 在集合和交/并操作构成的半格中,给定任意两个集 合 G E N , K I L L GEN, KILL GEN,KILL,函数 f ( S ) = ( S − K I L L ) ∪ G E N f(S)=(S-KILL) \cup GEN f(S)=(S−KILL)∪GEN为单调函数。
5 数据流分析单调框架
对于2和3是同一类问题,可以用数据流分析通用的框架(数据流分析单调框架)导出不同的算法。对于逆向分析,变换控制流图方向再应用单调框架即可。

算法伪代码: