数据结构练习程序

今天朋友托我写一份程序，大二本科生的数据结构课程实验。要是以前的话，肯定先要定义图的邻接表结构，图的输入输出操作，图的遍历，写了很多代码。但是现在也仅仅越简洁越实用越好，这可能是由于时过境迁，人的心境也就变了。

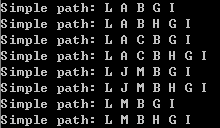
问题描述：图的路径遍历要比结点遍历具有更为广泛的应用。写一个路径遍历算法，求出从结点L到结点I中途不过结点K的所有简单路径。（图的存储结构没有要求）

/* ==============================================
*   Simple path
*   Author:[email protected]
*    2015.12.14
*/
#include 
#include 
#include 

using namespace std;

typedef struct
{
    char data[13];              
    int  matrix[13][13];            
}Graph;

Graph g = {
    {'A','B','C','D','E','F','G','H','I','J','K','L','M'},
    {
        {0,1,1,0,0,1,0,0,0,0,0,1,0},
        {1,0,1,1,0,0,1,1,0,0,0,0,1},
        {1,1,0,0,0,0,0,0,0,0,0,0,0},
        {0,1,0,0,1,0,0,0,0,0,0,0,0},
        {0,0,0,1,0,0,0,0,0,0,0,0,0},
        {1,0,0,0,0,0,0,0,0,0,0,0,0},
        {0,1,0,0,0,0,0,1,1,0,1,0,0},
        {0,1,0,0,0,0,1,0,0,0,1,0,0},
        {0,0,0,0,0,0,1,0,0,0,0,0,0},
        {0,0,0,0,0,0,0,0,0,0,0,1,1},
        {0,0,0,0,0,0,0,1,0,1,0,0,0},
        {1,0,0,0,0,0,0,0,0,1,0,0,1},
        {0,1,0,0,0,0,0,0,0,1,0,1,0} 
    }
};

deque<int> path;

//i是出发,j是目标，k是不经过节点
void dfs(Graph g,int i,int j,int k)
{
    if(i == k || (path.end()!=find(path.begin(),path.end(),i)))
        return;

    path.push_back(i);

    if(i == j)
    {
        cout<<"Simple path: ";
        for(int n = 0;n< path.size(); n++)
        {   
            cout<" ";
        }
        cout<return;
    }

    for(int n = 0;n<13;n++)
    {
        if(g.matrix[i][n] == 1)
        {   
            dfs(g,n,j,k);
        }
    }

    path.pop_back();
}

int main()
{
    dfs(g,11,8,10);
    getchar();
}

运行结果是只有8条简单路径，简单路径是指没有回路的路径。