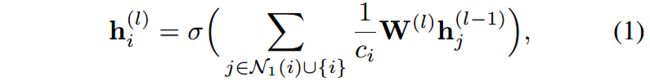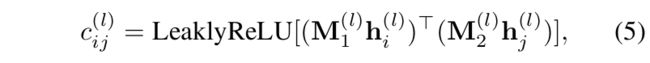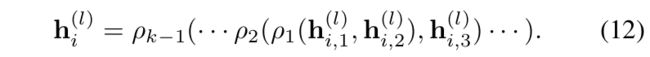【论文解读 AAAI2020|AliNet】KnowledgeGraph Alignment Network with Gated Multi-hop Neighborhood Aggregation

论文题目：Knowledge Graph Alignment Network with Gated Multi-hop Neighborhood Aggregation

论文来源：AAAI 2020 南京大学，阿里巴巴

论文链接：https://arxiv.org/abs/1911.08936

代码链接：https://github.com/nju-websoft/AliNet

关键词：知识图谱，嵌入学习，实体对齐，GNN，注意力机制，门机制

---

---

1 摘要

本文研究的是知识图谱的实体对齐问题。

由于GNN具有识别出同构子图的能力，因此应用于许多基于嵌入的实体对齐方法。

然而在知识图谱（KG）中，副本实体（counterpart entities）通常具有非同构的邻居结构，导致GNN为它们产生不同的表示。

为了解决这一问题，本文提出一个新的KG对齐网络，称为AliNet，旨在以端到端的方式缓解邻居结构的非同构问题。

由于模式（schema）的异质性，副本实体的直接邻居通常是不相似的。AliNet引入了远距离的（distant）邻居以扩展邻居结构的重叠部分。还使用了注意力机制强调有帮助的远距离邻居并减少噪声。然后使用门机制，对直接邻居和远距离邻居的信息进行聚合。

作者还提出了关系损失（relation loss）以改善实体的表示。

在5个实体对齐数据集上进行了实验，并进行了消融实验，证明了AliNet的有效性。

2 引言

（1）实体对齐

实体对齐是指从不同的KGs中找到指向真实世界中同一事物的实体。

近期，研究人员越来越关注于使用KG表示学习的方法来处理实体对齐问题，而不使用符号形式学习的方法。

表示学习指的是将KG编码到向量空间中，实体的语义关系信息可以通过嵌入操作学习到。嵌入操作有针对特定关系的translation，rotation等。

对于基于嵌入的实体对齐，通常使用实体嵌入间的距离来衡量实体间的相似性。

这种方法已经证明可以有效处理符号异质的问题，有助于单语言的和跨语言的实体对齐任务。

---

（2）GNN与实体对齐

GNN是可以对图结构的数据进行表示学习的强有力的模型，通过迭代地聚合目标节点自身以及节点邻居的表示以得到目标节点的表示。

近期有学者证明[1]GNN在识别同构的子图方面，具有和WL test（Weisfeiler-Lehman）相同的能力。

这为利用GNN实现不同KGs之间的实体对齐提供了理论依据，因为相似的实体通常具有相似的邻域。

已经有一些使用GNN进行基于嵌入的实体对齐的方法，并且取得了不错的效果。

---

（3）现有的基于GNN的实体对齐模型的缺点

不同的KGs有着异质的模式，并且有的KG是不完全的，因此副本实体（counterpart entities）通常有着并不相似的邻居结构，以图 1为例。

图 1中指向Kobe Bryant的两个实体的邻域是不一致的，邻居实体集合也是不同的。

有学者在基于BDpedia的基线数据集上进行了统计，结果表明大部分的对齐实体对都具有不同的邻域实体。

由于要对齐的实体具有不同的邻域结构，使用GNN就容易导致为这些实体生成不同的表示。

即使假定两个KGs是完全的，但由于模式的异质性，还是会使得副本实体具有不相似的邻域结构。如图 1中的United States of America，在Wikidata中是Kobe Bryant的一阶邻居，但在DBpedia中是Kobe Bryant的二阶邻居。

---

（4）作者提出

作者发现语义关联的信息可出现在副本实体的直接邻居或远距离邻居中，于是提出AliNet将直接邻居和远距离邻居的信息进行聚合。

每层AliNet都有多个函数来聚合多跳内的邻域信息。

为了减少噪声信息，作者进一步使用了注意力机制用于远距离邻居信息的聚合，以端到端的方式找到那些更重要的远距离邻居。

最终使用了门机制来组合多个聚合函数的输出表示，以得到当前层的隐层表示。

还设计了关系损失以调整实体的表示，并使得AliNet可以捕获到更特殊的结构信息，例如三角形的关系结构。

3 准备工作

3.1 GNN

GNN的主要思想是递归地聚合邻居的特征向量，以得到目标节点的表示。可使用不同的聚合策略对GNN进行各种变形。

（1）GCN

GNN的一个有名的变形就是Kipf等人提出的vanilla GCN。节点$i$在第$l$层的隐层表示定义为${\mathbf{h}}_i^{(l)}$，计算如下：

其中${\mathcal{N}}_1(\cdot )$表示给定实体的一阶邻居；${\mathbf{W}}^{(l)}$是第$l$层的权重矩阵；$c_i$是归一化常数；$\sigma (\cdot )$是激活函数。

vanilla GCN对目标节点自身在上一层的表示和当前层其邻居节点的表示进行mean pooling，来对目标节点进行编码。

---

（2）R-GCN

传统的GNN只考虑图中node-wise的连通性，忽视了边的标签，例如KG中的关系。R-GCN通过使用特定关系的权重矩阵对不同的邻居进行区分，解决了这一问题。节点的隐层表示计算如下：

其中${\mathbf{W}}_0^{(l)}$是节点自身的权重矩阵；${\mathbf{W}}_r^{(l)}$是用于有关系$r$的邻居${\mathcal{N}}_r(i)$的权重矩阵；$\mathcal{R}$是关系集合；$c_{i,r}$用于归一化。

3.2 知识图谱的实体对齐

将给定的KG记为$\mathcal{G}=(\mathcal{E},\mathcal{R},\mathcal{T})$，三个元素分别表示实体集合、关系集合以及三元组集合，其中$\mathcal{T}=\mathcal{E}\times \mathcal{R}\times \mathcal{E}$。

针对两个KG间的实体对齐问题，先给定两个KG：${\mathcal{G}}_1=({\mathcal{E}}_1,{\mathcal{R}}_1,{\mathcal{T}}_1)$和${\mathcal{G}}_2=({\mathcal{E}}_2,{\mathcal{R}}_2,{\mathcal{T}}_2)$，然后给定部分预对齐的实体对${\mathcal{A}}^{+}=\{(i,j)\in {\mathcal{E}}_1\times {\mathcal{E}}_2|i\equiv j\}$，其中$\equiv$表示对齐关系。这一任务的目的是通过实体的嵌入，找到剩余实体的对齐方式。

3.3 用于实体对齐的GNN

有GCN-Align, GMNN, MuGNN, RDGNN, AVR-GCN。

GCN-Align和GMNN是基于vanilla GCN设计的；RDGCN引入了对偶的关系图以增强vanilla GCN；AVG-GCN使用类似TransE的特定关系的translation操作，对R-GCN进行了扩展。

在聚合之前，使用关系向量从尾实体translate成头实体的表示。

作者认为这样针对特定关系的translation和R-GCN需要训练的参数量太大，计算成本高。而且上述模型均没有考虑到KG结构的非同构问题。

MuGNN考虑到了KG的结构不完全性，并提出了一个两步的操作：1）基于规则的KG补全；2）用于实体对齐的多通道GNN。但是学习到的规则依赖于关系对齐以缓解模式的异质性问题。

---

（1）Isomorphic structures are beneficial

若实体的邻域是同构的，GNN将会为实体学习到相同的表示。

作者发现在某些情况下，若两实体具有同构的邻域结构和仅部分预对齐的邻居表示，GNN也能构捕获到要对齐的其他邻域的相似性。图 2给出了一个例子：

为了简化我们考虑单层的GCN。通过最小化预对齐的实体间的欧式距离，我们可以使得预对齐的实体有相同的表示，例如${\mathbf{h}}_a^{(0)}={\mathbf{h}}_{a^{{}^{\prime }}}^{(0)},{\mathbf{h}}_b^{(0)}={\mathbf{h}}_{b^{{}^{\prime }}}^{(0)},{\mathbf{h}}_d^{(0)}={\mathbf{h}}_{d^{{}^{\prime }}}^{(0)}$，在理想情况下也有${\mathbf{h}}_a^{(1)}={\mathbf{h}}_{a^{{}^{\prime }}}^{(1)},{\mathbf{h}}_b^{(1)}={\mathbf{h}}_{b^{{}^{\prime }}}^{(1)},{\mathbf{h}}_d^{(1)}={\mathbf{h}}_{d^{{}^{\prime }}}^{(1)}$。

通过基于mean-pooling的聚合，有${\mathbf{h}}_b^{(1)}=\sigma ({\mathbf{W}}^{(1)}({\mathbf{h}}_b^{(0)}+{\mathbf{h}}_a^{(0)}+{\mathbf{h}}_c^{(0)})/3)$和${\mathbf{h}}_{b^{{}^{\prime }}}^{(1)}=\sigma ({\mathbf{W}}^{(1)}({\mathbf{h}}_{b^{{}^{\prime }}}^{(0)}+{\mathbf{h}}_{a^{{}^{\prime }}}^{(0)}+{\mathbf{h}}_{c^{{}^{\prime }}}^{(0)})/3)$，${\mathbf{h}}_c^{(0)}={\mathbf{h}}_{c^{{}^{\prime }}}^{(0)}$。最终副本实体会用相同的表示。

这就表示着，当给定部分预对齐的邻居时，实体间的对齐信息可以在不同的GNN层中以及不同的同构图中进行传播。

但是对于不同KG间的实体对齐，由于模式的异质性，让KG有同构的结构是不可能的。**图 2(ii)**就给出了非同构图结构的例子，其中$c$和$c^{{}^{\prime }}$由于它们的邻域结构不同，将会得到不同的表示。

---

（2）只有结构还不够

传统的GNN不能识别出特殊的子图结构，例如三角形图。**图 2(iii)**展示了一个简单的例子。

此例中使用mean-pooling聚合，由于4个实体有同构的邻居结构，应该得到$\mathbf{h}^{(1)}_a = \mathbf{h}^{(1)}_{a{’}} = \mathbf{h}^{(1)}_b = \mathbf{h}^{(1)}_{b{’}} $。

但是实际上，$a$和$b$在给定一个关系后是不同的实体，我们需要将关系纳入考虑。

尽管R-GCN在聚合函数中考虑到了关系，但它仍依赖于关系对齐，以用于识别相似的实体。

从（2）式可知，R-GCN需要为每个关系学习到一个权重矩阵。如果两个KG的关系没有预先对齐，则R-GCN中针对特定关系的聚合函数将不能传播实体的对齐信息。

---

（3）Compensation with distant neighborhood and relations

不同KG的模式异质性通常会使得副本实体的直接邻居和远距离邻居相混合。

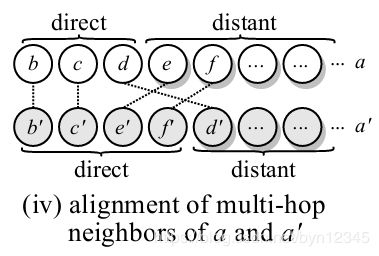
为了减少邻域结构中非同构性的影响，作者引入远距离邻居的信息，例如图 2 iv所示：

要对齐的两个实体$a$和$a^{{}^{\prime }}$的一阶邻居是不同的，只包含两对副本（counterpart）实体对$(b,b^{{}^{\prime }}),(c,c^{{}^{\prime }})$。$a$的一阶邻居$d$实际上是$a^{{}^{\prime }}$的远距离邻居$d^{{}^{\prime }}$，$a$的远距离邻居$e,f$可与$a^{{}^{\prime }}$的一阶邻居$e^{{}^{\prime }},f^{{}^{\prime }}$相对齐。

因此可以很容易地想到，如果我们能在聚合邻居信息以得到$a$的表示时考虑到$e,f$，在聚合邻居信息以得到$a^{{}^{\prime }}$的表示时考虑到$d^{{}^{\prime }}$，则GNN能学习到$a,a^{{}^{\prime }}$更相似的表示。

当然，不是所有的远距离邻居都是有帮助的，因此聚合时要使用注意力机制有所选择。

为了进一步增强AliNet的表示能力，还在不引入关系向量的前提下，考虑到了关系语义信息。

4 知识图谱对齐网络

在AliNet中，通过使用门机制控制$k$跳内邻居信息的聚合，来学习得到实体的表示。

接下来以$k=2$为例，即聚合一阶邻居和二阶邻居信息，实际中可以扩展到多跳。AliNet的网络结构如图 3所示。

4.1 Gated Multi-hop Neighborhood Aggregation

聚合一阶邻居信息使用vanilla GCN，进行式（1）所示的计算即可。

但是不能只聚合一阶邻居的信息。虽然有$L$层的GCN可以捕获到实体的$L-hop$的邻居信息，但这样一层一层地传播是低效的。

对于2-hop邻居的聚合，为了避免原始的GCN聚合在逐层传播中带来的噪声，我们引入了注意力机制。将给定实体的2-hop内的邻居集合表示为${\mathcal{N}}_2(\cdot )$。在第$l$层聚合实体$i$的2-hop邻居，得到隐层表示${\mathbf{h}}_{i,2}^{(l)}$计算如下：

其中${\alpha }_{ij}^{(l)}$是对于实体$i$和其邻居$j$的可学习的注意力权重。下一小节将介绍注意力权重的计算。

受神经网络中跳跃连接（skip connections）的启发，作者提出使用门机制以结合1-hop邻居和2-hop邻居。实体$i$在第$l$层的隐层表示${\mathbf{h}}_i^{(l)}$计算如下：

其中$g({\mathbf{h}}_{i,2}^{(l)})=\sigma (\mathbf{M}{\mathbf{h}}_{i,2}^{(l)}+\mathbf{b})$就像一个用来控制1-hop邻居和2-hop邻居相结合的门（gate）；$\mathbf{M},\mathbf{b}$分别是权重矩阵和偏置向量。

4.2 Attention for Distant Neighborhood

和实体距离较远的邻居数量和其一阶邻居数成指数关系。当然不是每个远距离邻居都对中心实体产生贡献，因此对于2-hop的邻居聚合，我们计算实体间的注意力权重，以强调那些有用的邻居。

GAT对每个注意力函数中的实体应用了一个共享的线性变换。然而，KG中的中心实体和其邻居可能是非常不同的，这样的共享变换会对区别它们带来负面影响。

因此，作者使用了两个矩阵${\mathbf{M}}_1^{(l)},{\mathbf{M}}_2^{(l)}$分别用于中心实体和其邻居的线性变换。

在第$l$层，实体$i,j$间的注意力权重$c_{ij}^l\in \mathbb{R}$计算如下：

使用softmax函数归一化注意力权重，以使得不同实体间可进行比较：

4.3 Contrastive Alignment Loss

最小化contrastive alignment loss使得对齐实体的表示距离小，非对齐的实体表示间的距离大：

其中${\mathcal{A}}^{-}$是随机替换预对齐的2个实体中的一个得到的负样本。$[\cdot {]}_{+}=max(0,\cdot )$。我们希望负样本实体的表示之间的距离大于$\lambda$。

已有的方法通常将最后一层的输出当做实体最终的表示，但是由于每一层都对传播对齐信息有所贡献，因此，作者使用了所有层的隐层表示，于是有：

其中$\oplus$表示拼接操作，$norm(\cdot )$是$L_2$正则化，以减少人为增加向量范数的繁琐优化过程。

4.4 Relation Semantics Modeling

KG提供了实体间的语义关联，我们要将关系事实中的语义信息合并到实体建模中。

如第3节中讨论的那样，为了进行实体对齐，R-GCN需要两个KG的结构高度相似或者关系是对齐的。作者借鉴了TransE中的translation assumption。为了避免参数过多，作者没有引入针对特定关系的嵌入。关系$r$的表示$\mathbf{r}$，可以通过和它相关的实体嵌入得到：

其中${\mathcal{T}}_r$是对于关系$r$的subject-object实体对。

然后最小化如下的关系损失，其中$\mathcal{R}$是两个KG的关系的总集合。

4.5 实现细节

（1）目标函数

AliNet最终的目标函数是contrastive alignment loss和relation loss的组合，目的是将关系语义信息整合到图结构中：

---

（2）向k-hop邻居的泛化

令${\rho }_1({\mathbf{h}}_{i,1}^{(l)},{\mathbf{h}}_{i,2}^{(l)})$为1-hop和2-hop邻居的结合，如式（4）。可使用$k-1$个门函数来递归地结合信息：

---

（3）邻居的增加

提出的gated multihop邻居聚合以端到端的方式扩展了实体的直接邻居。为了进一步实现此思想，作者提出了一个启发式的方法在预对齐的实体间添加边。特别地，如果$K{G}_1$中的两个实体$i,j$有一个边，但是它们对应的实体$i^{{}^{\prime }},j^{{}^{\prime }}$在$K{G}_2$中没有边，我们就添加一个边连接着两个实体。目的是希望通过添加这样的平衡边，以缓解非同构的问题。

---

（4）对齐预测

一旦训练AliNet，我们就可以基于cross-KG范围内实体表示之间的最近邻搜索来预测实体对齐。

给定一个$K{G}_1$中要被对齐的源实体$i$，它在$K{G}_2$中对应的副本实体为$i^{{}^{\prime }}=argmi{n}_{j\in {\mathcal{E}}_2}\pi ({\mathbf{h}}_i,{\mathbf{h}}_j)$。其中$\pi ()$是距离度量，例如欧式距离。我们使用结合的表示来衡量实体嵌入的距离。

5 实验

1、数据集

2、对比方法

（1）最近的基于嵌入的实体对齐模型

MTransE, IPTransE, JAPE, AlignE, GCN-Align, SEA, RSN, MuGNN.

最近的一些基于GNN的模型，比如GMNN和RDGCN将实体的surface信息纳入考虑，由于本文只依赖于结构的信息，因此不和这些方法进行比较。

---

（2）AliNet的变形

• AliNet (w/o rel. loss)：不优化关系损失；
• AliNet (w/o rel. loss & augment.)：不使用关系损失和邻居的增加。

---

（3）使用一些KG嵌入模型和GNN的变形作为baselines

1）KG嵌入模型：TransE, ConvE, RotatE

2）GNN：GCN, GAT, R-GCN

3、实验结果

实体对齐实验结果如表 1所示，AliNet在Hits@1和MRR上超越state-of-the-art。

6 总结

本文提出AliNet用于处理实体对齐任务，目的是缓解副本实体的邻域结构不同构的问题。

AliNet通过在每一层使用门机制，捕获到了多跳范围内的邻居信息。还使用了注意力机制用于聚合多跳的邻居信息以减少噪声。作者还提出了关系损失以增强AliNet的表达能力。

未来工作：将其他模态的副信息（side information）纳入考虑。

---

本文解决的是实体对齐问题，提出了AliNet。

（1）本文针对的问题

由于不同的KG模式不同，而且均有不完全性，要对齐的实体的邻居通常不是同构的，因此使用GNN会为中心实体生成不同的嵌入表示，因此无法实现实体对齐。

（2）提出的方法

作者认为即使不同KG中副本实体间的邻域不是同构的，但和实体有关的语义信息会在一定范围内的邻域中出现。例如在某个KG中中心实体的一阶邻居，可能是另一个KG中相对应的实体的二阶邻居。

基于上述思想，作者将一阶邻居和远距离邻居的信息聚合起来。以2-hop内的邻居为例（即远距离邻居指的是二阶邻居），对AliNet的pipeline进行回顾：

首先，使用GCN的公式得到聚合一阶邻居后的隐层表示，然后再对2-hop内所有的邻居信息进行聚合。注意与聚合一阶邻居不同的是，聚合2-hop内所有邻居时为每个邻居都分配了一个注意力权重，以衡量不同邻居的重要性，减少噪声。

接着使用门机制，对上述操作得到的两个隐层表示进行聚合，得到中心节点在该层网络中的最终的隐层表示。

需要注意的是，并不是直接使用网络最后一层输出的隐层表示作为KG中实体的最终表示，而是对所有层的隐层表示都进行了利用，得到KG中实体最终的表示。

在损失方面还考虑到了KG中关系的语义信息，引入了关系损失。

（3）引入注意力机制与GAT相比的不同

GAT在计算注意力权重时，对所有的实体共享一个线性变换。作者考虑到KG中中心实体和邻居有着很大的不同，于是对中心实体和其邻居使用了两个不同的线性变换。

（4）思考

在引入关系损失的部分，关系的嵌入就是通过三元组中两个实体的嵌入相减得到的（等式（9）），目标函数（等式（10））中还要最小化两个实体的嵌入之差再减去关系的嵌入，这里总感觉有点问题。但是实验结果显示优化关系损失后效果也确实提升了。

k-hop一般指的是k阶子图，也就是和中心节点距离小于等于k的邻居节点们组成的子图。对1-hop的邻居进行了聚合，又对2-hop的邻居进行聚合，是不是说一阶邻居被计算了两次，感觉有点信息的冗余。没看过代码，可能是我想多了。

不足：没有利用到三元组的语义信息，生成的表示缺少区分性。IJCAI2020有一篇文章以此为动机，已经超越了此模型。

这里的提到的文章忘记出处了[捂脸]，这句话应该是后来编辑上去的，忘记留下什么记录了，目前丝毫都想不起来了，甚至有点怀疑是不是编辑的时候搞错文章了。看到的朋友先忽略吧，或者知道些什么的朋友也欢迎评论留言。

参考文献

[1] Morris, C.; Ritzert, M.; Fey, M.; Hamilton, W. L.; Lenssen, J. E.; Rattan, G.; and Grohe, M. 2019. Weisfeiler and leman go neural: Higher-order graph neural networks. In AAAI, 4602–4609.