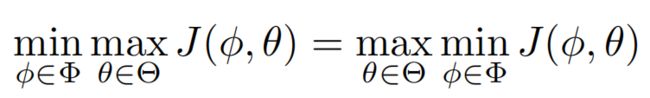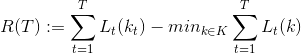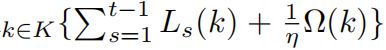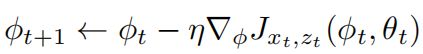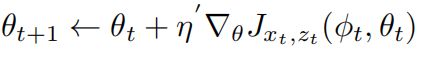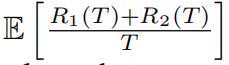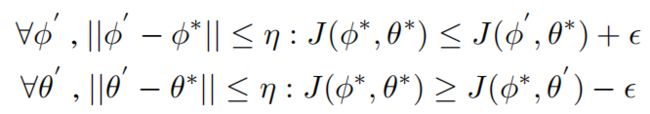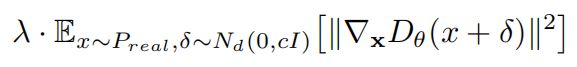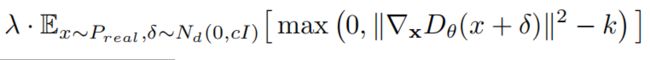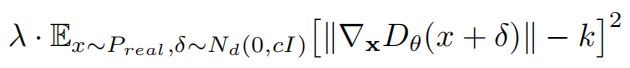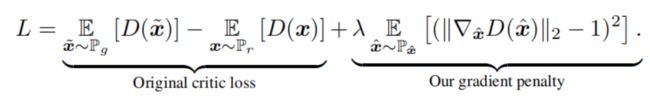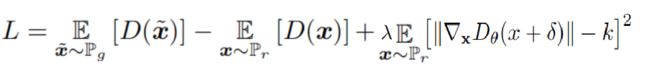On Convergence and Stability of GANs（小白学GAN ：十四）

原文链接：https://arxiv.org/pdf/1705.07215v5.pdf

简介

背景：我们在训练GAN时，常常以生成分布与训练分布的拟合程度最高（即距离最小）来作为优化的目标，然而这往往导致我们训练出的GAN仅是局部拟合，而全局上并未与目标分布靠近，于是作者基于此提出了使用regret minimization来优化的DRAGAN 。

核心思想：将原始GAN的consistent minimization改为regret minimization，来防止尖锐梯度的出现，保证GAN在优化时的稳定性。

基础结构

基础概念

Sion定理

若,且为紧凸集，为凸集，在第一个自变量中是凹的，在第二个自变量中是凸的，则有：

形象点上个图，可以看到满足上述条件后，这两个变量的优化顺序是不会影响最后得到的值的。

无悔算法

给定一系列凸损失函数，,按时间序列获得,如果,则这个序列是无悔的

                                                        

从上面的式子来看无悔算法就是在优化时，保证优化进程和得到的LOSS在同一阶上，当LOSS与迭代进程相匹配时就是无悔的。

将无悔算法与GAN的LOSS结合起来，那么视为第K轮的生成器损失函数，视为第K轮的判别器损失函数，那么T轮博弈之后：

                                       

假设是生成器与判别器的平衡值，那么当生成器与判别器分别“有悔”时，即，可以得到下面的式子：

也就是说，生成器的最佳解是,判别器的最佳解是,也就是达到“有悔”之前，我们就已经找到最佳的模型。但是，实际情况中很难做到生成器与判别器同时刚好达到“有悔”，所以我们用近似项来作为整体的“有悔”项。

正则化

使用如下的正则规则：

其中为正则函数，为学习率。

若原始的GAN目标函数表示为

那么考虑到x，z的期望，也可以表示为

判别器的优化

生成器的优化

那么在没有优化到最佳值之前，我们可以使用来作为误差边界。

局部均衡

防止模式溃散的出现。

梯度惩罚

简单来说，就是作者发现出现模式溃散时，都是判别器梯度迅速出现“尖刺”时，也就是判别器梯度迅速下降，优化速度超过生成器的速度，导致生成器将多种分布都映射到一个模式上。那么引入梯度惩罚项，来限制判别器优化速度让它等等生成器：

上述方法确实可以稳定GAN的训练，但是噪声惩罚项的引入干扰了判别器的性能导致，最终生成器的分布也会取拟合噪声，于是改进为

即对噪声的大小进行限制，当生成分布与随机分布已经在靠近时，即生成器向判别器拟合时，不引入噪声惩罚。

本文最终采用的是如下的惩罚机制，经过实验时，效果较好：

耦合惩罚

作者提到其实对判别器的梯度惩罚，在WGAN_GP中也使用了耦合惩罚项，可以使得生成器学习到更好的分布，但是他们是在全局上做的，本文是在局部数据分布上做的，那么对比下有什么区别：

WGAN_GP中判别器LOSS

作者提出的DRAGAN的判别器LOSS：

最大的不同就是，惩罚项至于真实数据有关，而不受已学习分布的影响，已学习的生成分布与已经学习的数据是相关的，所以某种意义上来说，它是与全局的样本都是相关的，而这样修改后惩罚项就仅与局部的样本相关了。

代码实践

参考链接：https://github.com/jfsantos/dragan-pytorch

# coding: utf-8

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import argparse

import numpy as np
import torch
from torch.autograd import Variable, grad
from torch.nn.init import xavier_normal
from torchvision import datasets, transforms
import torchvision.utils as vutils

def xavier_init(model):
    for param in model.parameters():
        if len(param.size()) == 2:
            xavier_normal(param)


if __name__ == '__main__':
    batch_size = 128
    z_dim = 100
    h_dim = 128
    y_dim = 784
    max_epochs = 1000
    lambda_ = 10

    train_loader = torch.utils.data.DataLoader(
        datasets.MNIST('../../data', train=True, download=True,
                       transform=transforms.Compose([
                           transforms.ToTensor()
                       ])),
        batch_size=batch_size, shuffle=True, drop_last=True)
    test_loader = torch.utils.data.DataLoader(
        datasets.MNIST('../../data', train=False, transform=transforms.Compose([
                           transforms.ToTensor()
                       ])),
        batch_size=batch_size, shuffle=False, drop_last=True)

    generator = torch.nn.Sequential(torch.nn.Linear(z_dim, h_dim),
            torch.nn.Sigmoid(),
            torch.nn.Linear(h_dim, y_dim),
            torch.nn.Sigmoid())

    discriminator = torch.nn.Sequential(torch.nn.Linear(y_dim, h_dim),
            torch.nn.Sigmoid(),
            torch.nn.Linear(h_dim, 1),
            torch.nn.Sigmoid())

    # Init weight matrices (xavier_normal)
    xavier_init(generator)
    xavier_init(discriminator)

    opt_g = torch.optim.Adam(generator.parameters())
    opt_d = torch.optim.Adam(discriminator.parameters())

    criterion = torch.nn.BCELoss()
    X = Variable(torch.FloatTensor(batch_size, y_dim))
    z = Variable(torch.FloatTensor(batch_size, z_dim))
    labels = Variable(torch.FloatTensor(batch_size))

    # Train
    for epoch in range(max_epochs):
        for batch_idx, (data, target) in enumerate(train_loader):
            X.data.copy_(data)

            # Update discriminator
            # train with real
            discriminator.zero_grad()
            pred_real = discriminator(X)
            labels.data.fill_(1.0)
            loss_d_real = criterion(pred_real, labels)
            loss_d_real.backward()

            # train with fake
            z.data.normal_(0, 1)
            fake = generator.forward(z).detach()
            pred_fake = discriminator(fake)
            labels.data.fill_(0.0)
            loss_d_fake = criterion(pred_fake, labels)
            loss_d_fake.backward()

            # gradient penalty
            alpha = torch.rand(batch_size, 1).expand(X.size())
            x_hat = Variable(alpha * X.data + (1 - alpha) * (X.data + 0.5 * X.data.std() * torch.rand(X.size())), requires_grad=True)
            pred_hat = discriminator(x_hat)
            gradients = grad(outputs=pred_hat, inputs=x_hat, grad_outputs=torch.ones(pred_hat.size()),
                    create_graph=True, retain_graph=True, only_inputs=True)[0]
            gradient_penalty = lambda_ * ((gradients.norm(2, dim=1) - 1) ** 2).mean()
            gradient_penalty.backward()

            loss_d = loss_d_real + loss_d_fake + gradient_penalty
            opt_d.step()

            # Update generator
            generator.zero_grad()
            z.data.normal_(0, 1)
            gen = generator(z)
            pred_gen = discriminator(gen)
            labels.data.fill_(1.0)
            loss_g = criterion(pred_gen, labels)
            loss_g.backward()
            opt_g.step()

            print('[%d/%d][%d/%d] Loss_D: %.4f Loss_G: %.4f'
                  % (epoch, max_epochs, batch_idx, len(train_loader),
                     loss_d.item(), loss_g.item()))

            if batch_idx % 100 == 0:
                vutils.save_image(data,
                        'samples/real_samples.png')
                fake = generator(z)
                vutils.save_image(gen.data.view(batch_size, 1, 28, 28),
                        'samples/fake_samples_epoch_%03d.png' % epoch)

minist测试结果