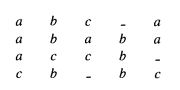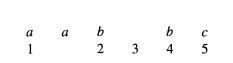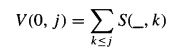生物信息学算法笔记
入门生物信息学,选了一条比较难的路,直接从底层算法开始,这种做法其实不太明智。读了"Algorithms on Strings, Trees and Sequences",一本厚厚的算法书,后半部分其实读得有些粗糙。今天读完了第一遍,总的来说还是有些收获,将笔记记录于此。
全书总共分为四部分:基本字符串算法、后缀树算法、非精确匹配算法、映射与测序。基本字符串算法以KMP为代表,这个是基本功,而且很久之前的博客竟然正好记录了这个算法;后缀树算法在前几篇博客专门进行了描述;非精确匹配以动态规划为基础,这个也算是老朋友,近期的博客也专门讨论了这个主题,本文也将继续延伸这个话题;映射与测序,也将在此进行讨论。因此本文分为两大部分:非精确匹配的进一步讨论、映射与测序。
整理得有点乱,甚至有些部分直接用的截图,以后有机会再进一步整理。本文的主要目的是记录一些核心思路,方便今后回顾。
非精确匹配的进一步讨论
Refining Core String Edits and Alignments
空间优化:Computing alignments in only linear space
那么转移方程可以写成如下形式:
由转移方程可知,空间可压缩一维。
时间优化:Faster algorithms when the number of differences is bounded
之前在后缀树的应用里讨论过 k-mismatch的问题,这里讲讨论 k-difference 的问题,区别在于:前者只允许替换,而后者还允许增删。
两类特殊的 k-difference问题:
k-difference global alignment
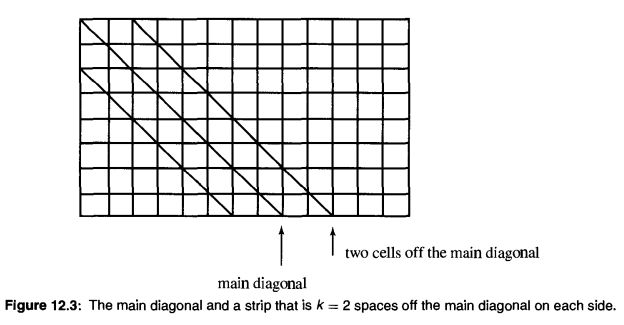
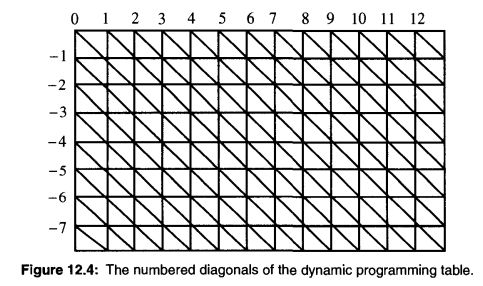
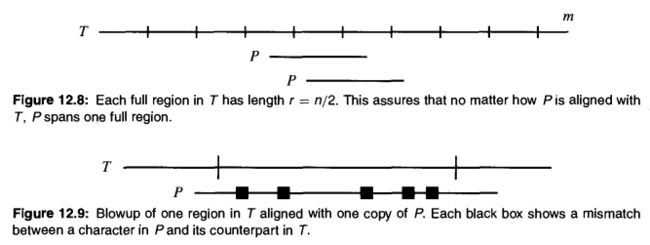
下图为动态规划转移表,(0, 0)开始的对角线为主对角线,其左下方的为负对角线,其右上方的为正对角线。若最多允许k 个不同,则最终结果必然从 -k对角线 至 k对角线 之间的条带中的状态推导而来,因为这个条带以外的状态,其匹配已经出现了超过k个不同的字符。
Exclusion methods: fast expected running time
先排除一些不可能匹配成功的片段,进而优化计算速度。总的思路如下:
具体的算法很多,这里描述两个典型的:BYP算法、CL算法。
BYP算法:
CL算法:
Yet more suffix trees and more hybrid dynamic programming
有两个典型的问题。
The P-against-all problem Given strings P and T, compute the edit distance between P and every substring T' of T.
The threshold all-against-all problem Given strings P and T and a threshold d, find every pair of substrings P' of P and T' of T such that the edit distance between P' and T' is less than d.
思路:
对于P-against-all 问题,可以先构建出T的后缀树,在这个后缀树上计算与P的编辑距离,即在后缀树上进行深度优先的动态规划。优点在于可以省去很多重复计算。对于all-against-all 问题,请参考书上相关章节(12.4.2)。
LCS 的快速算法
其实就是将LCS 问题转化为LIS 问题,而LIS 可以在O(N*logN) 内实现,因此LCS 也变成了O(N*logN)。
LIS的O(N*logN)算法
D为数字序列,D的一个cover定义为D的下降序列的集合,且这个集合涵盖了S的序列全部。cover的大小为这个集合中下降序列的个数。
如:S= 5, 3, 4, 9, 6, 2, 1, 8, 7, 10。则 {5, 3, 2, 1}; {4}; {9, 6}; {8, 7}; {10} 是S 的一个cover,这个cover的大小为5。
根据定理12.5.4可知,构建最小cover的过程可以采用二分搜索法,因此最终的时间复杂度为O(N*logN)。
如何将LCS 问题转归为LIS 问题
定义:r(i)表示S1[i]这个字符 在S2中出现过多少次,r=∑r(i)。
定义:t(x)表示x 这个字符在S2 中出现的位置的列表,并且顺序为从大到小排列。
举例:S1=abacx, S2=baabca,则 r=3+2+3+1+0=9,t(a)=(6,3,2),t(b)=(4,1)。
基于S1构建列表SS:对于S1中每个位置i,用t(S1[i])列表进行替换,最终可以得到长度为r的新列表SS。
举例:对于以上S1和S2,构建的SS为:(6,3,2,4,1,6,3,2,5)。
定理:SS的LIS 与S1和S2的LCS对应。
拓展:多个字符串的LCS问题,可以用类似的方法转换成LIS问题。
Extending the Core Problem
主要讨论了3个问题:Parametric sequence alignment 、Computing suboptimal alignments 和 Chaining diverse local alignments。此处主要看下 Parametric sequence alignment。
实际工作中,会遇到不少带参数的字符串匹配问题。
Multiple String Comparison
将字符串对齐问题(非精确匹配)从2个字符串拓展到多个字符串,即为多字符串比较问题。实际上从生物学角度来看,多个字符串的问题与两个字符串的问题是相反的。
两个生物学事实。
The first fact of biological sequence analysis: In biomolecular sequences (DNA, RNA, or amino acid sequences), high sequence similarity usually implies significant functional or structural similarity.
The second fact of biological sequence comparison: Evolutionarily and functionally related molecular strings can differ significantly throughout much of the string and yet preserve the same three-dimensional structure(s), or the same two-dimensional substructure(s) (motifs, domains), or the same active sites, or the same or related dispersed residues (DNA or amino acid).
第一个事实是两个字符串问题的生物学基础,第二个事实是间隔问题及多个字符串问题的生物学基础。
Multiple String Comparison的3大应用:蛋白家族(及超级家族)的呈现、DNA或蛋白质中与结构(或功能)相关的保守片段的识别和呈现、DNA或蛋白质的进化史的推导(进化树的形式呈现)(进化树的内容本文略去)。
Family and superfamily representation
常用的呈现方式有3种:profile representations, consensus sequence representations, and signature representations.
profile representations
定义:Given a multiple alignment of a set of strings, a profile for that multiple alignment specifies for each column the frequency that each character appears in the column. A profile is sometimes also called a weight matrix in the biological literature.
举例:下图是对齐后的结果。
对每列的各个字符计算出现频率,得到下表,即为profile representations。
对于新字符串aabbc,其相对于profile的最佳对齐方式应当如下图所示。
解决思路:
For a character y and column j, let p(y, j) be the frequency that character y appears in column j of the profile, and let S(x, j) denote ∑y[s(x, y) x p(y, j)], the score for aligning x with column j.
Let V(i, j) denote the value of the optimal alignment of substring S[l..i] with the first j columns of C.
初始条件:
转移方程:
signature representations
一些保守序列可以用类似于正则表达式的形式表示,这种表示即为signature representations。如某个motif 可表示如下:
[&H][&A]D[DE]xn[TSN]x4[QK]Gx7[&A]
"&" stands for any amino acid from the group (/, L,V, M, F, Y, W), "x" stands for any amino acid, and alternative amino acids are bracketed together. The subscript on x gives the length of a permitted substring; "n" indicates that any length substring is possible.
consensus sequence representations
找一个公认的有代表性序列,作为该蛋白家族的呈现,即为consensus sequence representations。
Steiner consensus strings
D(Si, Sj) denotes the weighted edit distance of strings Si, and Sj.
Given a set of strings S, and given another string S', the consensus error of a string S' relative to S is E(S') = ∑si∈s D(S' Si). Note that S' need not be from S.
Given a set of strings S, an optimal Steiner string S* for
Multiple string alignments 的计算
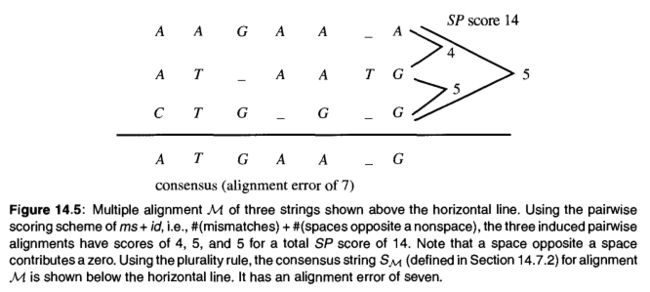
给定一种对齐方式,对于其中任意两个字符串计算分值,最后将所有分值求和,得到总分值SP(sum of pairs),目标是使得SP最小化。
这个问题虽然可以使用动态规划准确求解,但是时间复杂度是指数级的,这是个NP 完全问题。书上给出了三个字符串的SP求解示例程序(pascal语言)。
此外,书中还给出了bounded-error approximation 的方法(界定误差的近似求法)——center star法。感兴趣的请直接参考章节14.6.2。
Sequence Databases and Their Uses
这个部分介绍了常见的几个数据库 及其背后的部分算法,如:FASTA、BLAST、PAM、BLOCKS和BLOSUM 等。
本文此处不进行记录,直接看书吧,或者在实际操作中去领会。
映射与测序
Mapping
概念
以下概念摘自网络资源(具体来源不详)。
遗传图谱(genetic maps):某一物种的染色体图谱(也就是我们所知的连锁图谱),显示所知的基因和/或遗传标记的相对位置,而不是在每条染色体上特殊的物理位置。采用遗传学分析方法将基因或其它DNA标记按一定的顺序排列在染色体上,这一方法包括杂交实验,家系分析。标记间的距离(遗传图距)用减数分裂中的交换频率来表示,单位为厘摩Centi-Morgan, cM), 每单位厘摩定义为1%交换率。遗传学图谱的解像度(分辨率)低,大约只能达到100万碱基对(1Mb)的水平。
物理图谱(physical maps):顾名思义,是DNA中一些可识别的界标(如限制性酶切位点、基因等)在DNA上的物理位置,图距是物理长度单位,如染色体的带区、核苷酸对的数量等。
两者异同:
①遗传图谱是基于重组频率,物理图谱是基于直接测量的DNA结构。
②减数分裂重组的频率并不统一沿大多数染色体。有一些热点和冷点在重组和/或突变。热点和冷点会导致相当大的格律失真时,遗传图谱和物理地图并排排列时。
③遗传图谱表示的是基因或标记间的相对距离,以重组值表示,单位CM
④物理图谱表示的是基因或标记间的物理距离,距离的单位为长度单位,如μm或者碱基对数(bp或kp)等。
简而言之,前者是描述的基因相对位置,后者是具体的碱基位置。
STS是序列标记位点(sequence-tagged site)的缩写,是指染色体上位置已定的、核苷酸序列已知的、且在基因组中只有一份拷贝的DNA短片断,一般长200bp-500bp。它可用PCR方法加以验证。将不同的STS依照它们在染色体上的位置依次排列构建的图为STS图。在基因组作图和测序研究时,当各个实验室发表其DNA测序数据或构建成的物理图时,可用STS来加以鉴定和验证,并确定这些测序的DNA片段在染色体上的位置;还有利于汇集分析各实验室发表的数据和资料,保证作图和测序的准确性。
EST是表达序列标签(expressed sequence tag)的缩写,在人类基因组测序工作中,有一个区别于"全基因组战略"的"cDNA战略",即只测定转录的DNA序列。此时,须从cDNA文库中获取一些长为300-400各碱基序列作为表达序列标签,其作用相当于全基因组测序时的序列标记位点(STS),即可用来验证和整理不同实验室发表的cDNA测序资料。两端又重叠序列的EST可以装配成全长的cDNA序列。特定的EST序列有时可代表特定的cDNA。
辐射性杂交制图技术(radiation-hybrid mapping)是一种体细胞杂交技术,适用于构建人类基因组长范围内的高分辨率连续物理图谱。利用高剂量的X射线将候选染色体打断成若干片段,含有这种片段的细胞可与仓鼠细胞形成杂交克隆。在这种杂交中,人类染色体片段被插入到仓鼠染色体的中间部分,因此大部分克隆片段在进行有丝分裂时处于稳定的状态。
利用类似于遗传重组原理和最大似然性的统计学方法来计算存在于DNA片段上的多态性或非多态性标记之间的断点频率,以此估计标记之间的距离,并建立人类基因组拷贝库---体细胞杂交系统。可根据不同要求构建出断裂程度不同的多套拷贝,从而得到不同分辨率的放射杂交图。总之,辐射性杂交是建立在受到X射线照射的供体细胞与非放射线处理的受体细胞融合基础上的一种体细胞遗传学方法。
Physical mapping:STS-content mapping and ordered clone libraries
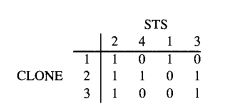
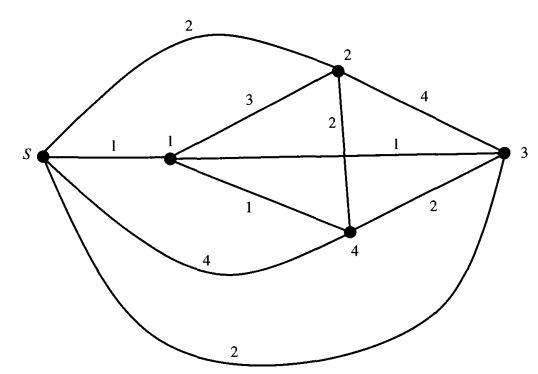
下图中有4个STS,其真实顺序如下图所示,但是这个顺序我们事先是不知道的,需要结合后面的计算去推断出来。下图还包含3个clone片段。
匹配出3个片段各自包含了哪些STS之后,可得到下图的01矩阵,由于事先并不知道各个STS的排列顺序,因此此时顺序是打乱的。
找出一种排列顺序,使得每行中的1具有连续性,成为一个独立的块。这也就实现了STS顺序的重建。
Physical mapping: radiation-hybrid mapping
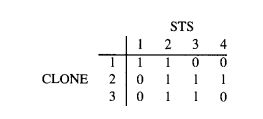
这个是加强版的STS顺序问题,每个细胞具有多个不相邻的片段,如下图所示。
由于不知道真实顺序,匹配各个STS后,得到以下的01矩阵。
重建STS顺序的方法:traveling salesman tour。
构建无向图,边 e(u ,v)表示编号为u与v的STS 列,之间有几个01值不相同。为了方便起见,此处略去5-7这3个STS,构建的无向图如下所示。
找一个从S出发且经历所有节点的路径,且经历的路径总长度(即所有e(u ,v)之和)最短,这条路径的顺序很可能就是STS的顺序。上图求得的最短路径为:S-3-1-4-2,长度为6,对应的连续块的数量为4。遗憾的是并不是真实的顺序1234(真实顺序的连续块的数量竟然更大…)。(期待更好的方法解决这个问题)
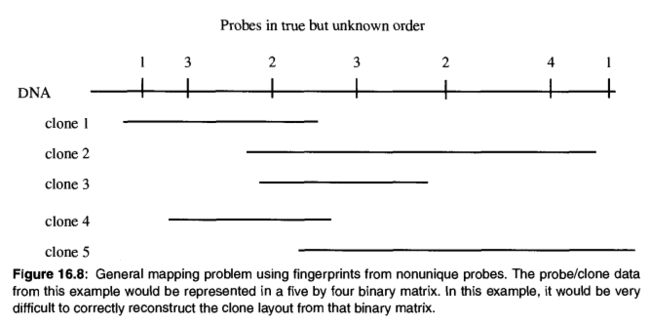
Physical mapping: fingerprinting for general map construction
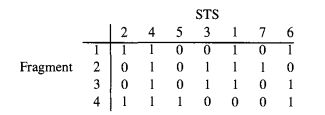
探针问题与STS问题类似,但是探针在DNA序列中可以重复出现,如下图所示。
上图最终构造的01矩阵是5*4的规模,重建出其真实顺序的难度比较大。有不少文章提出过解决方案,书中描述了一种贪心方法,请参考章节16.8。
Sequencing
引物步移(primer walking):一种长链DNA测序的策略。根据已测出的序列结构设计测序引物,按第一轮测序得出的新序列,再设计引物进行第二轮测序,如此重复,直至获得全序列。
嵌套缺失法(Nested deletion) : 该法基本原理是基因DNA链的一端与载体相连固定,另一端在核酸外切酶的作用下随着时间的延长,较匀速地消化变短。这样可人为获得一组长度不等(如依次相差200~250 bp)的从一端开始缺失的DNA片段。它们从缺失端开始的测序可读部分宛如拉杆天线的一段套管,最长片段(未被核酸外切酶作用的DNA)相当于拉杆天线的全长,它的可读部分相当于拉杆天线的最远端的套管。这些DNA片段从长至短虽然依次相差200~250 bp,但从缺失端可读取300~500 bp序列,重叠部分便可准确无误地将相邻段重合拼接。测序中,它们的引物相同因而可以很方便地首先读出引物序列,找出该DNA片段的起始,起始段DNA序列也正是前一较长DNA片段可读的后一部分序列,它们如此重叠嵌套,便可准确测出整个基因(或长DNA链)的序列。
书中还提到了 "Top-down, bottom-up sequencing( the picture using YACs)" 、"Shotgun DNA sequencing" 等方法的描述。这些东西将会重新学习一遍,之后会系统地学一下WGS的知识。
----------------------------------------------------------------------------------
2018/10/02 补充
学习路上吃了很多亏,无法及时的将所学的东西运用起来。时间不够用啊,我的专业不是这个方向,有很多事情等着我去做呢,这个时候最高效的方式是先了解如何使用,然后练习即可。学有余力再去专研其理论知识(人生苦短)。以今天的经验教训来看,本文的这些东西(包括之前字符串的非精确匹配、3篇后缀树系列博客),以后不要再纠结了,尽量不要把时间花在这方面。