推荐系统技术内幕(四):算法篇之召回与融合
基于内容的推荐算法
基于内容的推荐算法,建立在这样一个基本假设上:用户会喜欢他喜欢的物品的相似物品。
这是一个很朴素的假设,也比较符合人性,比如如果喜欢看喜剧之王,大概率也会喜欢大话西游。在这个假设的基础上,我们的推荐算法的过程就是:将找到用户喜欢的物品的相似物品,如果用户还没有消费过,就推荐给他。
原理是不是很简单。
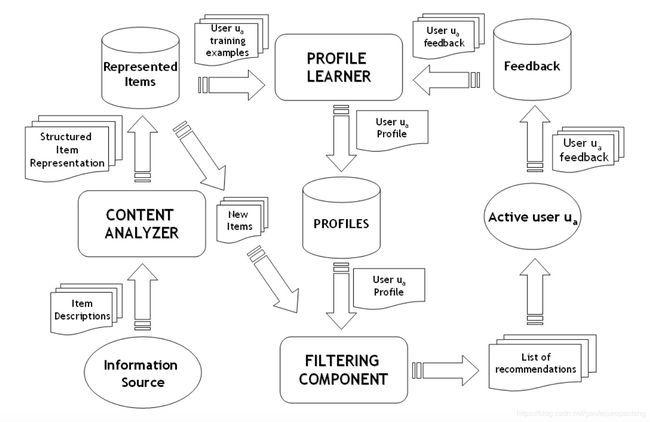
在新物品加入的时候,还没有积累任何的用户行为数据,这时候只能靠基于内容的推荐了。基于内容的推荐的基础是对物品本身信息的挖掘。
- 内容源的信息经过内容分析后,得到结构化的内容库以及内容模型,也就是物品画像;这部分算法在推荐系统技术内幕(二):算法篇之物品画像中讲解过。
- 用户的反馈数据,结合内容库,经过用户画像学习,得到用户画像,这部分的算法在推荐系统技术内幕(三):算法篇之用户画像中讲解过。
- 新物品加入后,进过内容模型的处理,得到新物品画像,结合用户画像,就可以进过推荐算法进行推荐了。得到展示的物品,有了用户反馈数据,可以用来继续训练用户画像,如此周而复始。
注意,这里说基于内容的推荐系统,不需要用户反馈数据,是指候选的物品可以没有用户相关的反馈,而不是说整个系统不需要用户反馈数据。相反,整个系统是需要用户反馈数据去学习用户画像的。
内容分析的输出,包括结构化内容库和内容模型,新物品加入后就是利用这些内容模型,得出新物品的画像信息的,这些内容模型包括:
- 分词、命名实体识别模型
- 关键词抽取模型
- 分类、聚类模型
- 主题学习模型
- 嵌入学习模型
基于内容的推荐,常采用的推荐方式是,将物品画像、用户画像,结合用户的行为日志,转换为训练样本,通过评分预估或行为预估为目标,训练出预估模型。
样本的特征包括物品画像特征,上下文特征特征,用户画像特征;样本的标注通过用户反馈日志自动标注。基于内容的推荐模型常用的有逻辑回归(Logistic Regression)和梯度提升数(GBDT).
基于协同过滤的推荐算法
协同过滤应该是推荐系统领域最著名的算法。
协同过滤算法背后的假设是:用户会喜欢与他相似用户喜欢的物品,用户会喜欢他们喜欢的物品的相似物品。对应的,协同过滤算法分两种:
- user-based: 首先找到目标用户的相似用户,然后将相似用户喜欢的、目标用户还未消费的物品,推荐给目标用户
- item-based: 首先找到目标用户消费的物品的相似物品,然后将这些物品中还未被目标用户消费过的物品,推荐给用户
协同过滤在寻找相似用户或相似物品的时候,依赖的数据并非基于内容的分析的产出,而是因为在经过内容推荐后,熬过了冷启动借点,这时候已经积累的用户反馈数据。从用户行为日志里提取的用户与物品间的关系,一般一矩阵形式存在,称为用户物品关系矩阵。关系的值可以是是否消费记录或则用户对物品的评分。
协同过滤算法是一个比较大算法范畴,一般又可以划分为:
- memory-based: 基于记忆的协同过滤是基础,直接通过用户的消费历史,推荐相似的物品,或相似用户消费的物品。
- model-based: 基于模型的系统过滤,通过用户的消费历史数据,训练出模型,通过模型推荐物品。
Memory Based
首先看比较基础的基于记忆的协同过滤,这类算法又细分为user-based和item-based。先看user-based。算法的主要步骤是:
1. 从关系矩阵构造用户向量,用户向量的纬度是物品的个数,向量的每个纬度的取值表示用户是否消费过该物品或则是否喜欢该物品。
2. 计算用户向量之间的相似度。相似度的计算方法有很多中,比如常见的有:
- 欧氏距离
d ( s , t ) = ∑ i n ( s i − t i ) 2 d(s,t)=\sqrt{\sum_{i}^{n}(s_i - t_i)^2} d(s,t)=i∑n(si−ti)2
欧氏距离的取值范围是 [ 0 , + ∞ ) [0, +\infty) [0,+∞),可以通过下面公式转化为 ( 0 , 1 ] (0,1] (0,1]之间的相似度:
s i m ( s , t ) = 1 d ( s , t ) + 1 sim(s,t) = \frac{1}{d(s,t) + 1} sim(s,t)=d(s,t)+11
- 余弦相似度:
s i m ( s , t ) = ∑ i n ( s i t i ) ∑ i n s i 2 ∑ i n t i 2 sim(s,t)=\frac{\sum_{i}^{n}(s_it_i)}{\sqrt{\sum_{i}^{n}s_i^2}\sqrt{\sum_{i}^{n}t_i^2}} sim(s,t)=∑insi2∑inti2∑in(siti)
- jaccard相似度,适用于计算两个集合相似度
s i m ( S , T ) = ∣ S ∩ T ∣ ∣ S ∪ T ∣ sim(S,T)=\frac{|S\cap T|}{|S\cup T|} sim(S,T)=∣S∪T∣∣S∩T∣
其中, S , T S,T S,T表示两用户喜欢的物品组成的集合。
- Pearson相关系数
s i m ( s , t ) = ∑ i n ( s i − s ‾ ) ( t i − t ‾ ) ∑ i n ( s i − s ‾ ) 2 ∑ i n ( t i − t ‾ ) 2 sim(s,t)=\frac{\sum_{i}^{n}(s_i-\overline s)(t_i-\overline t)}{\sqrt{\sum_{i}^n(s_i-\overline s)^2}\sqrt{\sum_{i}^n(t_i-\overline t)^2}} sim(s,t)=∑in(si−s)2∑in(ti−t)2∑in(si−s)(ti−t)
3. 每个用户会有n个相邻用户,通过相似度值选取最相似的若干用户。这个选取的过程可以是Top N选取,也可以通过设计相似度阈值。
4. 相似用户喜欢的每一个物品x,过滤掉用户已经消费过的物品,计算一个推荐分数,计算公式为:
R ( u , x ) = ∑ v k s i m ( u , v ) ⋅ R ( v , x ) ∑ v k s i m ( u , v ) R(u, x)=\frac{\sum_{v}^ksim(u,v)\cdot R(v,x)}{\sum_{v}^{k}sim(u,v)} R(u,x)=∑vksim(u,v)∑vksim(u,v)⋅R(v,x)
其中u表示推荐目标用户,有k个相邻用户。
item-Based的算法,过程比较类似,算法过程为:
1.从关系矩阵构造物品向量,向量的纬度是用户的数量,每个纬度的值表示用户是否喜欢此物品或则用户对物品的评分。
2.计算物品间的相似度,计算可以采用欧氏相似度或则余弦相似度。
3.更具物品间的相似度,为没一个物品产生一个相似物品集合,也可以为用户产生一个集合,方法是对每个物品x,计算一个推荐分数,计算方法为:
R ( u , x ) = ∑ i n s i m ( x , i ) ⋅ R ( u , i ) ∑ i n s i m ( x , i ) R(u,x)=\frac{\sum_i^nsim(x,i)\cdot R(u,i)}{\sum_i^nsim(x,i)} R(u,x)=∑insim(x,i)∑insim(x,i)⋅R(u,i)
其中,用户u有n个喜欢的物品。
Model Based
基于记忆的协同过滤,对关系矩阵的利用比较基础,关系矩阵可以是评分矩阵,也可以是消费行为矩阵。Model Based适用于评分矩阵,其基本思路是通过以后的评分数据,学习一个模型,将关系矩阵中空缺值填上。
评分预测问题最著名的就是基于矩阵分解的算法。矩阵分解的过程就是将原始的评分举证分解成两个矩阵相乘的过程:
R m × n = U m × k V n × k T R_{m\times n} = U_{m\times k}V_{n\times k}^T Rm×n=Um×kVn×kT
矩阵分解是一个算法范畴,有很多中分解算法,比较基础的SVD算法。
SVD算法的过程,基本思路就是不断调整 U m × n , V n × k U_{m\times n},V_{n\times k} Um×n,Vn×k的值,使相乘结果不断接近 R m × n R_{m\times n} Rm×n的过程,是一个标准的机器学习过程。
基础的SVD的损失函数定义为:
c o s t = ∑ u ∑ v ( r u v − p u ⋅ q v T ) 2 cost = \sum_{u}\sum_v(r_{uv}-p_u\cdot q_v^T)^2 cost=u∑v∑(ruv−pu⋅qvT)2
其中 p u p_u pu表示用户u的向量表示,纬度为 k k k,所以用户的向量表示构成矩阵 U m × k U_{m\times k} Um×k, q v q_v qv表示物品v的向量表示,纬度也为 k k k,所以物品的向量表示构成了矩阵 V n × k V_{n\times k} Vn×k.
一般的为了增强模型的泛化能力,会记上正则化项:
c o s t = ∑ u ∑ v ( r u v − p u ⋅ q v T ) 2 + λ ( ∣ ∣ ∣ p u ∣ ∣ 2 + ∣ ∣ q v ∣ ∣ 2 ) cost = \sum_{u}\sum_v(r_{uv}-p_u\cdot q_v^T)^2 + \lambda(|||p_u||^2 + ||q_v||^2) cost=u∑v∑(ruv−pu⋅qvT)2+λ(∣∣∣pu∣∣2+∣∣qv∣∣2)
有了损失函数,接下来要解决的问题就是学习算法的问题,一般会采用基于梯度的学习算法或则交替最小二乘算法。
在基础的SVD基础上,有很多扩展的算法,比如加入时间,历史,偏移等等信息的考虑。
另外,R. R. Salakhutdinov等人提出了一种使用受限玻尔兹曼机(RBM)来进行协同过滤的方法,这里就不展开介绍了。
推荐的融合
前面说过,很多推荐系统包括两个主要的阶段:召回和融合,召回阶段就是通过以上介绍和没介绍的种种推荐算法,产生候选集,融合就是对前阶段的输出进行统一的排序,产生最终的推荐结果。
推荐的融合方式分为两种:
- 基于规则: 别小看规则,前面说过,做好推荐系统,还需要很好的领域知识,领域知识的存在形式之一就是规则,最好的推荐系统一定领域知识与数据驱动算法的结合。比如可以根据具体的业务,制定多种推荐结果的加权规则、或切换规则、融合规则。例如什么情况下用内容推荐的结果,什么情况下用协同推荐的结果,或则两种推荐结果都用,怎么混合推荐结果,各取TOP多少,等等。
- 自动融合:以具体的业务指标为导向的,比如指标可以是CTR,或停留时长,等等,学习出一个模型,通过模型产生统一的推荐结果。常用的算法模型有GBDT,FM,Wide And Deep等等,关于模型的具体介绍,这里也不再展开了。
冷启动问题
推荐领域的冷启动问题,一般指代两类问题:
- 新物品:新加入系统的新物品还未被展示过,未产生任何用户的反馈数据,如何对新物品进行推荐的问题被称为物品冷启动问题。
- 新用户:类似的,新加入系统的新用户未在系统内产生任何的消费行为,如何向这类新用户推荐物品的问题被称为用户冷启动问题。
物品冷启动问题,一般采用基于内容的推荐算法,在介绍基于内容的推荐的时候,已经介绍了。而用户冷启动问题是推荐领域并未完全解决的问题,可以从下面几个层面的方法可以尝试。
算法层面:
- 兴趣试探算法,比如Bandit,增强学习等等。这类算法的思路,简单来说就是一边推荐,一边根据反馈数据修正推荐策略。
数据层面:
- 利用用户基本信息,比如用户的地域位置,使用的手机型号,等等
- 主动询问兴趣,很多个性化的产品在第一次使用的时候,都会主动让用户选择一些兴趣点或则具体的感兴趣的物品
- 引入第三方数据
领域知识层面:
- 用优质的物品:一般来说,在不知道推荐哪些物品的情况下,稳妥的策略就是推荐高质量的优质物品,这个原则在很多领域的推荐系统都是成立的,比如信息流推荐,视频推荐。
探索与利用(Explore & Exploit)
人性是复杂的,人类是好恶有一定的稳定性,同时人类也是善变的,一直为用户推荐目前喜欢的物品绝非最优策略,推荐系统需要探索和发现用户的新兴趣点。所以推荐需要除了会利用目前的兴趣点产生推荐物品外,还会为了试探用户的未知兴趣点为用户推荐试探的物品。
探索与利用问题也是推荐系统经典问题之一,目前的实现的方式不尽相同,从简单的随机试探,到基于强化学习的试探都有尝试,可以参考相关的资料,这里不展开详述了。
推荐系统的演进
目前为止介绍了很多推荐相关算法,有关于数据挖掘的,有基于内容的、协同过滤的、Bandit、增强学习等等的推荐的,林林总总。但实际当中,没有一个系统是一步到位的,都会经历一个由起步到完善的演进的过程。那么在演进的过程中就有一个重要的实际问题,也就是决定先做什么,后做什么的问题,本文给出一些建议。
- 起步阶段:百废待兴,系统的一切从零开始,包括数据的收集、处理和存储,服务间的通信,模型的训练和使用;一般来说开源社区版的工具就可以满足我们系统的需求,此阶段的重点是快速利用开源工具搭建起推荐系统的基础版本。模型可以考虑使用简单的LR模型或决策树类的模型,并且可以采用离线训练的方式。另外要做好物品的画像分析等数据挖掘工作,此阶段的推荐主要依赖的特征是数据挖掘输出的结构化的知识,也就是基于内容的推荐。
- 发展阶段:度过了起步阶段的系统,接下来的发展阶段的目标,就是提高推荐的效果;数据层面,可以精细化数据处理,包括数据的采样、去噪等;特征层面可以尝试更多的高级特征,包括预训练向量,动态特征等等。模型方面,因为积累是一定的用户数据,可以尝试更多更复杂的模型,比如基于协同过滤的和深度学习的模型,同时可以尝试在线学习模型。
- 完善阶段:一方面,随着用户量的进一步增长,开源工具难以满足越来越复杂的业务场景的需求,组件的定制化需求凸现出来。另一方面,为了进一步提高推荐的效果,领域知识与推荐算法的结合,是推荐系统发展的一个方向,尽管这个方向存在一定的争议性,争议来自于算法至上和人机结合的争论。