irober

数据科学案例4 线性回归之房价预测（代码）

数据科学案例4 房价预测（代码）

Step1:描述性统计

1、简单预处理
2、因变量（price）

1）因变量直方图
2）查看因变量的均值、中位数和标准差等更多信息
3）查看因变量最高和最低的两条观测

2、自变量

1）整体来看（连续变量与分类变量分开）
2) 变量dist
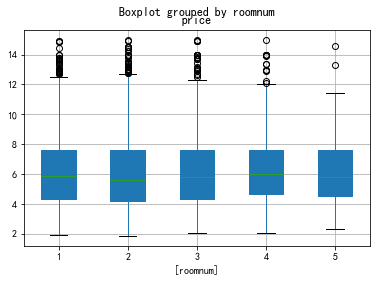
3) roomnum
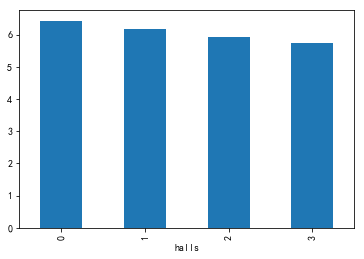
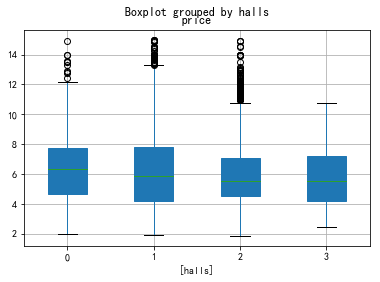
4) halls
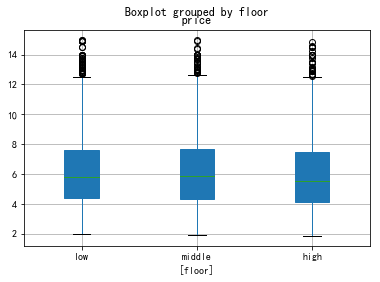
5) floor
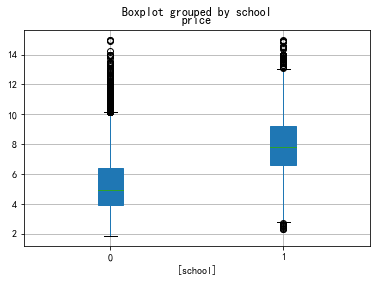
6) subway+school （stack2dim函数）
7) AREA

Steo2:建模

1、首先检验每个解释变量是否和被解释变量独立（get_sample（）函数）
3 线性回归模型
4、对数线性模型
5、有交互项的对数线性模型，城区和学区之间的交互作用

import numpy as np 
import pandas as pd
import math
import statsmodels.formula.api as ols
import seaborn as sns
from scipy import stats
from numpy import corrcoef,array
get_ipython().magic('matplotlib inline')

datall = pd.read_csv(r'.\data\sndHsPr.csv',encoding='gbk')  #读入清洗过后的数据
data0 = datall
data0['price'] = datall.price/10000 #价格单位换成万元

Step1:描述性统计

1、简单预处理

data0.describe(include='all').T #基本描述

	count	unique	top	freq	mean	std	min	25%	50%	75%	max
dist	16210	6	fengtai	2947	NaN	NaN	NaN	NaN	NaN	NaN	NaN
roomnum	16210	NaN	NaN	NaN	2.16619	0.809907	1	2	2	3	5
halls	16210	NaN	NaN	NaN	1.22141	0.532048	0	1	1	2	3
AREA	16210	NaN	NaN	NaN	91.7466	44.0008	30.06	60	78.83	110.517	299
floor	16210	3	middle	5580	NaN	NaN	NaN	NaN	NaN	NaN	NaN
subway	16210	NaN	NaN	NaN	0.827822	0.377546	0	1	1	1	1
school	16210	NaN	NaN	NaN	0.303085	0.459606	0	0	0	1	1
price	16210	NaN	NaN	NaN	6.11518	2.22934	1.8348	4.28123	5.7473	7.60998	14.9871

dict1 = {
        "chaoyang":"朝阳",
        "haidian":"海淀",
        "fengtai":"丰台",
        "dongcheng":"东城",
        "shijingshan":"石景山",
        "xicheng":"西城"
}
data0.dist = data0.dist.apply(lambda x : dict1[x])
data0.head()

	dist	roomnum	halls	AREA	floor	subway	school	price
0	朝阳	1	0	46.06	middle	1	0	4.8850
1	朝阳	1	1	59.09	middle	1	0	4.6540
2	海淀	5	2	278.95	high	1	1	7.1662
3	海淀	3	2	207.00	high	1	1	5.7972
4	丰台	2	1	53.32	low	1	1	7.1268

2、因变量（price）

import matplotlib.pyplot as plt

# 中文乱码的处理
plt.rcParams['font.sans-serif'] = [u'SimHei']
plt.rcParams['axes.unicode_minus'] = False

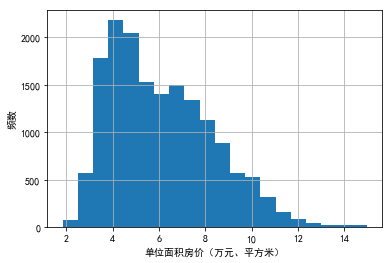
1）因变量直方图

# 法一：
data0.price.hist(bins=20)
plt.xlabel("单位面积房价（万元、平方米）")
plt.ylabel("频数")

Text(0, 0.5, '频数')

2）查看因变量的均值、中位数和标准差等更多信息

print(data0.price.agg(['mean','median','std']))
print(data0.price.quantile([0.25,0.5,0.75]))

mean      6.115181
median    5.747300
std       2.229336
Name: price, dtype: float64
0.25    4.281225
0.50    5.747300
0.75    7.609975
Name: price, dtype: float64

3）查看因变量最高和最低的两条观测

pd.concat([data0[data0.price==min(data0.price)],data0[data0.price==max(data0.price)]])

	dist	roomnum	halls	AREA	floor	subway	school	price
2738	丰台	2	2	100.83	high	0	0	1.8348
12788	西城	3	1	77.40	low	1	0	14.9871

2、自变量

（dist+roomnum+halls+floor+subway+school+AREA）

1）整体来看（连续变量与分类变量分开）

for i in range(7):
    if i != 3:  #分离出连续变量AREA
        print(data0.columns.values[i],":")
        print(data0[data0.columns.values[i]].agg(['value_counts']).T)
        print("=======================================================================")
    else:
        continue
print('AREA:')
print(data0.AREA.agg(['min','mean','median','max','std']).T)

dist :
                丰台    海淀    朝阳    东城    西城   石景山
value_counts  2947  2919  2864  2783  2750  1947
=======================================================================
roomnum :
                 2     3     1    4    5
value_counts  7971  4250  3212  675  102
=======================================================================
halls :
                  1     2    0   3
value_counts  11082  4231  812  85
=======================================================================
floor :
              middle  high   low
value_counts    5580  5552  5078
=======================================================================
subway :
                  1     0
value_counts  13419  2791
=======================================================================
school :
                  0     1
value_counts  11297  4913
=======================================================================
AREA:
min        30.060000
mean       91.746598
median     78.830000
max       299.000000
std        44.000768
Name: AREA, dtype: float64

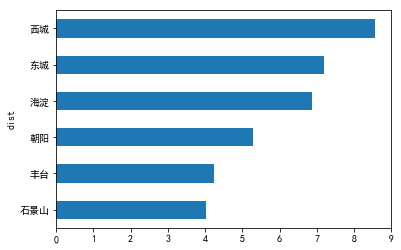
2) 变量dist

Series.plot

#频次统计
data0.dist.value_counts().plot(kind = 'pie')   #绘制柱柱形图
data0.dist.agg(['value_counts'])
#dat0.dist.value_counts()

	value_counts
丰台	2947
海淀	2919
朝阳	2864
东城	2783
西城	2750
石景山	1947

data0.price.groupby(data0.dist).mean().sort_values(ascending= True).plot(kind = 'barh')  #不同城区的单位房价面积均值情况

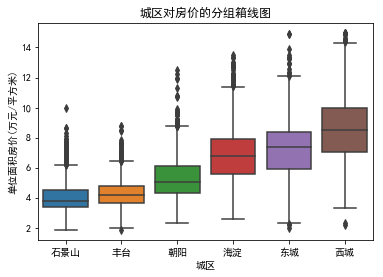
data1=data0[['dist','price']]
#在做箱线图时需要做以下操作
data1.dist=data1.dist.astype("category")
data1.dist.cat.set_categories(["石景山","丰台","朝阳","海淀","东城","西城"],inplace=True) #为了好看，按顺序画出
#dat1.sort_values(by=['dist'],inplace=True)
sns.boxplot(x='dist',y='price',data=data1)
#dat1.boxplot(by='dist',patch_artist=True)
plt.ylabel("单位面积房价(万元/平方米)")
plt.xlabel("城区")
plt.title("城区对房价的分组箱线图")

Text(0.5, 1.0, '城区对房价的分组箱线图')

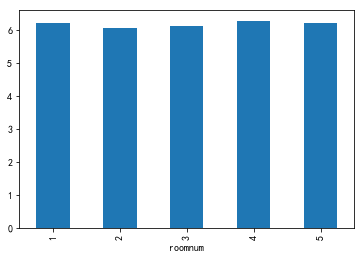
3) roomnum

#不同卧室数的单位面积房价差异不大
data2=data0[['roomnum','price']]
data2.price.groupby(data2.roomnum).mean().plot(kind='bar')
data2.boxplot(by='roomnum',patch_artist=True)

4) halls

#厅数对单位面积房价有轻微影响
data3=data0[['halls','price']]
data3.price.groupby(data3.halls).mean().plot(kind='bar')
data3.boxplot(by='halls',patch_artist=True)

5) floor

#不同楼层的单位面积房价差异不明显
data4=data0[['floor','price']]
data4.floor=data4.floor.astype("category")
data4.floor.cat.set_categories(["low","middle","high"],inplace=True)
# dat6.sort_values(by=['floor'],inplace=True)
data4.boxplot(by='floor',patch_artist=True)
# dat6=data0[['floor','price']]
# dat6.price.groupby(dat6.floor).mean().plot(kind='bar')
# dat6.boxplot(by='floor',patch_artist=True)

d:\Anaconda3\lib\site-packages\pandas\core\generic.py:5096: SettingWithCopyWarning: 
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead

See the caveats in the documentation: http://pandas.pydata.org/pandas-docs/stable/indexing.html#indexing-view-versus-copy
  self[name] = value

6) subway+school （stack2dim函数）

def stack2dim(raw, i, j, rotation = 0, location = 'upper left'):
    '''
    此函数是为了画两个维度标准化的堆积柱状图
    要求是目标变量j是二分类的
    raw为pandas的DataFrame数据框
    i、j为两个分类变量的变量名称，要求带引号，比如"school"
    rotation：水平标签旋转角度，默认水平方向，如标签过长，可设置一定角度，比如设置rotation = 40
    location：分类标签的位置，如果被主体图形挡住，可更改为'upper left'
    
    '''
    import math
    data_raw = pd.crosstab(raw[i], raw[j])
    data = data_raw.div(data_raw.sum(1), axis=0)  # 交叉表转换成比率，为得到标准化堆积柱状图
    
    # 计算x坐标，及bar宽度
    createVar = locals()
    x = [0] #每个bar的中心x轴坐标
    width = [] #bar的宽度
    k = 0
    for n in range(len(data)):
        # 根据频数计算每一列bar的宽度
        createVar['width' + str(n)] = data_raw.sum(axis=1)[n] / sum(data_raw.sum(axis=1))
        width.append(createVar['width' + str(n)])  
        if n == 0:
            continue
        else:
            k += createVar['width' + str(n - 1)] / 2 + createVar['width' + str(n)] / 2 + 0.05
            x.append(k)  
    
    # 以下是通过频率交叉表矩阵生成一列对应堆积图每一块位置数据的数组，再把数组转化为矩阵
    y_mat = []
    n = 0
    for p in range(data.shape[0]):
        for q in range(data.shape[1]):
            n += 1
            y_mat.append(data.iloc[p, q])
            if n == data.shape[0] * 2:
                break
            elif n % 2 == 1:
                y_mat.extend([0] * (len(data) - 1))
            elif n % 2 == 0:
                y_mat.extend([0] * len(data))

    y_mat = np.array(y_mat).reshape(len(data) * 2, len(data))
    y_mat = pd.DataFrame(y_mat)  # bar图中的y变量矩阵，每一行是一个y变量
    
    # 通过x，y_mat中的每一行y，依次绘制每一块堆积图中的每一块图
    createVar = locals()
    for row in range(len(y_mat)):
        createVar['a' + str(row)] = y_mat.iloc[row, :]
        if row % 2 == 0:
            if math.floor(row / 2) == 0:
                label = data.columns.name + ': ' + str(data.columns[row])
                plt.bar(x, createVar['a' + str(row)],
                        width=width[math.floor(row / 2)], label='0', color='#5F9EA0')
            else:
                plt.bar(x, createVar['a' + str(row)],
                        width=width[math.floor(row / 2)], color='#5F9EA0')
        elif row % 2 == 1:
            if math.floor(row / 2) == 0:
                label = data.columns.name + ': ' + str(data.columns[row])
                plt.bar(x, createVar['a' + str(row)], bottom=createVar['a' + str(row - 1)],
                        width=width[math.floor(row / 2)], label='1', color='#8FBC8F')
            else:
                plt.bar(x, createVar['a' + str(row)], bottom=createVar['a' + str(row - 1)],
                        width=width[math.floor(row / 2)], color='#8FBC8F')

    plt.title(j + ' vs ' + i)
    group_labels = [data.index.name + ': ' + str(name) for name in data.index]
    plt.xticks(x, group_labels, rotation = rotation)
    plt.ylabel(j)
    plt.legend(shadow=True, loc=location)
    plt.show()

print(pd.crosstab(data0.subway,data0.school))
sub_sch=pd.crosstab(data0.subway,data0.school)
sub_sch = sub_sch.div(sub_sch.sum(1),axis = 0)
sub_sch

school     0     1
subway            
0       2378   413
1       8919  4500

school	0	1
subway
0	0.852024	0.147976
1	0.664655	0.335345

stack2dim(data0, i="subway", j="school")

#地铁、学区的分组箱线图
data5=data0[['subway','price']]
data6=data0[['school','price']]
data5.boxplot(by='subway',patch_artist=True)
data6.boxplot(by='school',patch_artist=True)

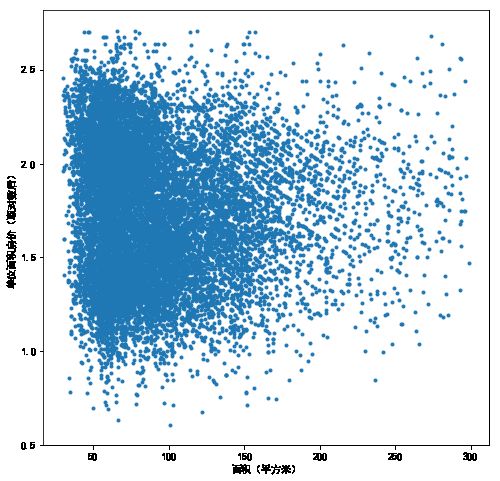
7) AREA

datA=data0[['AREA','price']]
plt.scatter(datA.AREA,datA.price,marker='.')
#求AREA和price的相关系数矩阵
dat1=array(datA['price'])
dat2=array(datA['AREA'])
datB=array([dat1,dat2])
corrcoef(datB)

array([[ 1.        , -0.07395475],
       [-0.07395475,  1.        ]])

#看到从左至右逐渐稀疏的散点图,第一反应是对Y取对数
#房屋面积和单位面积房价（取对数后）的散点图
datA['price_ln'] = np.log(datA['price'])  #对price取对数
plt.figure(figsize=(8,8))
plt.scatter(datA.AREA,datA.price_ln,marker='.')
plt.ylabel("单位面积房价（取对数后）")
plt.xlabel("面积（平方米）")

Text(0.5, 0, '面积（平方米）')

#求AREA和price_ln的相关系数矩阵
dat1=array(datA['price_ln'])
dat2=array(datA['AREA'])
datB=array([dat1,dat2])
corrcoef(datB)

array([[ 1.        , -0.05811827],
       [-0.05811827,  1.        ]])

#房屋面积和单位面积房价（取对数后）的散点图
datA['price_ln'] = np.log(datA['price'])  #对price取对数
datA['AREA_ln'] = np.log(datA['AREA'])  #对price取对数
plt.figure(figsize=(8,8))
plt.scatter(datA.AREA_ln,datA.price_ln,marker='.')
plt.ylabel("单位面积房价（取对数后）")
plt.xlabel("面积（平方米）")

#求AREA_ln和price_ln的相关系数矩阵
dat1=array(datA['price_ln'])
dat2=array(datA['AREA_ln'])
datB=array([dat1,dat2])
corrcoef(datB)

array([[ 1.       , -0.0939296],
       [-0.0939296,  1.       ]])

Steo2:建模

1、首先检验每个解释变量是否和被解释变量独立（get_sample（）函数）

由于原始样本量太大，无法使用基于P值的构建模型的方案，因此按照区进行分层抽样
#逐个检验变量的解释力度
“”"
不同卧室数的单位面积房价差异不大
客厅数越多，单位面积房价递减
不同楼层的单位面积房价差异不明显
地铁房单价高
学区房单价高
“”"
“”“大致原则如下（自然科学取值偏小、社会科学取值偏大）：
n<100 alfa取值[0.05,0.2]之间
100 500 “””

def get_sample(df, sampling="simple_random", k=1, stratified_col=None):
    """
    对输入的 dataframe 进行抽样的函数

    参数:
        - df: 输入的数据框 pandas.dataframe 对象

        - sampling:抽样方法 str
            可选值有 ["simple_random", "stratified", "systematic"]
            按顺序分别为: 简单随机抽样、分层抽样、系统抽样

        - k: 抽样个数或抽样比例 int or float
            (int, 则必须大于0; float, 则必须在区间(0,1)中)
            如果 0 < k < 1 , 则 k 表示抽样对于总体的比例
            如果 k >= 1 , 则 k 表示抽样的个数；当为分层抽样时，代表每层的样本量

        - stratified_col: 需要分层的列名的列表 list
            只有在分层抽样时才生效

    返回值:
        pandas.dataframe 对象, 抽样结果
    """
    import random
    import pandas as pd
    from functools import reduce
    import numpy as np
    import math
    
    len_df = len(df)
    if k <= 0:
        raise AssertionError("k不能为负数")
    elif k >= 1:
        assert isinstance(k, int), "选择抽样个数时, k必须为正整数"
        sample_by_n=True
        if sampling is "stratified":
            alln=k*df.groupby(by=stratified_col)[stratified_col[0]].count().count() # 有问题的
            #alln=k*df[stratified_col].value_counts().count() 
            if alln >= len_df:
                raise AssertionError("请确认k乘以层数不能超过总样本量")
    else:
        sample_by_n=False
        if sampling in ("simple_random", "systematic"):
            k = math.ceil(len_df * k)
        
    #print(k)

    if sampling is "simple_random":
        print("使用简单随机抽样")
        idx = random.sample(range(len_df), k)
        res_df = df.iloc[idx,:].copy()
        return res_df

    elif sampling is "systematic":
        print("使用系统抽样")
        step = len_df // k+1          #step=len_df//k-1
        start = 0                  #start=0
        idx = range(len_df)[start::step]  #idx=range(len_df+1)[start::step]
        res_df = df.iloc[idx,:].copy()
        #print("k=%d,step=%d,idx=%d"%(k,step,len(idx)))
        return res_df

    elif sampling is "stratified":
        assert stratified_col is not None, "请传入包含需要分层的列名的列表"
        assert all(np.in1d(stratified_col, df.columns)), "请检查输入的列名"
        
        grouped = df.groupby(by=stratified_col)[stratified_col[0]].count()
        if sample_by_n==True:
            group_k = grouped.map(lambda x:k)
        else:
            group_k = grouped.map(lambda x: math.ceil(x * k))
        
        res_df = df.head(0)
        for df_idx in group_k.index:
            df1=df
            if len(stratified_col)==1:
                df1=df1[df1[stratified_col[0]]==df_idx]
            else:
                for i in range(len(df_idx)):
                    df1=df1[df1[stratified_col[i]]==df_idx[i]]
            idx = random.sample(range(len(df1)), group_k[df_idx])
            group_df = df1.iloc[idx,:].copy()
            res_df = res_df.append(group_df)
        return res_df

    else:
        raise AssertionError("sampling is illegal")

# 由于原始样本量太大，无法使用基于P值的构建模型的方案，因此按照区进行分层抽样
dat01=get_sample(data0, sampling="stratified", k=400, stratified_col=['dist'])

import statsmodels.api as sm
from statsmodels.formula.api import ols

print("dist的P值为:%.4f" %sm.stats.anova_lm(ols('price ~ C(dist)',data=dat01).fit())._values[0][4])
print("roomnum的P值为:%.4f" %sm.stats.anova_lm(ols('price ~ C(roomnum)',data=dat01).fit())._values[0][4])#明显高于0.001->不显著->独立
print("halls的P值为:%.4f" %sm.stats.anova_lm(ols('price ~ C(halls)',data=dat01).fit())._values[0][4])#高于0.001->边际显著->暂时考虑
print("floor的P值为:%.4f" %sm.stats.anova_lm(ols('price ~ C(floor)',data=dat01).fit())._values[0][4])#高于0.001->边际显著->暂时考虑
print("subway的P值为:%.4f" %sm.stats.anova_lm(ols('price ~ C(subway)',data=dat01).fit())._values[0][4])
print("school的P值为:%.4f" %sm.stats.anova_lm(ols('price ~ C(school)',data=dat01).fit())._values[0][4])

dist的P值为:0.0000
roomnum的P值为:0.8225
halls的P值为:0.0812
floor的P值为:0.0074
subway的P值为:0.0000
school的P值为:0.0000

pr0 = sm.stats.anova_lm(ols('price ~ C(roomnum)',data=dat01).fit())
pr0

	df	sum_sq	mean_sq	F	PR(>F)
C(roomnum)	4.0	7.653530	1.913383	0.380849	0.822463
Residual	2395.0	12032.476868	5.023999	NaN	NaN

pr0._values[0][4]

0.8224626405021388

###厅数不太显著，考虑做因子化处理，变成二分变量，使得建模有更好的解读
###将是否有厅bind到已有数据集
dat01['style_new']=dat01.halls
dat01.style_new[dat01.style_new>0]='有厅'
dat01.style_new[dat01.style_new==0]='无厅'
dat01.head()

	dist	roomnum	halls	AREA	floor	subway	school	price	style_new
1014	东城	3	1	69.64	low	1	1	8.6876	有厅
12591	东城	2	1	81.27	middle	1	1	9.0440	有厅
5429	东城	3	1	56.73	high	1	0	7.9324	有厅
11788	东城	1	1	48.21	middle	1	0	4.7708	有厅
6726	东城	5	2	295.90	middle	1	0	5.7452	有厅

#对于多分类变量，生成哑变量，并设置基准--完全可以在ols函数中使用C参数来处理虚拟变量
data=pd.get_dummies(dat01[['dist','floor']])
data.head()

	dist_东城	floor_high	floor_low	floor_middle
1014	1	0	1	0
12591	1	0	0	1
5429	1	1	0	0
11788	1	0	0	1
6726	1	0	0	1

#哑变量的个数为k-1(k为分类变量的个数，这里选取了价格最便宜的石景山和楼层高)
data.drop(['dist_石景山','floor_high'],axis=1,inplace=True)#这两个是参照组-在线性回归中使用C函数也可以
data.head()

	dist_东城	floor_low	floor_middle
1014	1	1	0
12591	1	0	1
5429	1	0	0
11788	1	0	1
6726	1	0	1

#生成的哑变量与其他所需变量合并成新的数据框
dat1=pd.concat([data,dat01[['school','subway','style_new','roomnum','AREA','price']]],axis=1)
dat1.head()

	dist_东城	floor_low	floor_middle	school	subway	style_new	roomnum	AREA	price
1014	1	1	0	1	1	有厅	3	69.64	8.6876
12591	1	0	1	1	1	有厅	2	81.27	9.0440
5429	1	0	0	0	1	有厅	3	56.73	7.9324
11788	1	0	1	0	1	有厅	1	48.21	4.7708
6726	1	0	1	0	1	有厅	5	295.90	5.7452

3 线性回归模型

dat1

	dist_东城	dist_丰台	dist_朝阳	dist_海淀	dist_西城	floor_low	floor_middle	school	subway	style_new	roomnum	AREA	price
1014	1	0	0	0	0	1	0	1	1	有厅	3	69.64	8.6876
12591	1	0	0	0	0	0	1	1	1	有厅	2	81.27	9.0440
5429	1	0	0	0	0	0	0	0	1	有厅	3	56.73	7.9324
11788	1	0	0	0	0	0	1	0	1	有厅	1	48.21	4.7708
6726	1	0	0	0	0	0	1	0	1	有厅	5	295.90	5.7452
6954	1	0	0	0	0	1	0	0	1	有厅	3	215.53	4.6398
2690	1	0	0	0	0	0	0	0	1	有厅	2	85.00	3.5295
1927	1	0	0	0	0	0	1	0	1	有厅	1	44.37	7.6629
3609	1	0	0	0	0	0	0	0	1	有厅	1	46.23	4.8021
7658	1	0	0	0	0	0	0	1	1	有厅	1	36.82	10.3205
12812	1	0	0	0	0	1	0	0	1	有厅	2	140.00	10.4715
2751	1	0	0	0	0	0	0	0	1	有厅	2	57.00	6.3158
15340	1	0	0	0	0	1	0	0	1	有厅	2	72.00	6.0834
7478	1	0	0	0	0	0	1	1	1	有厅	2	43.97	11.0303
10875	1	0	0	0	0	0	1	0	1	有厅	4	243.76	7.9997
1666	1	0	0	0	0	0	1	1	1	有厅	2	82.45	8.2475
7487	1	0	0	0	0	0	1	1	1	有厅	2	62.32	8.1836
3907	1	0	0	0	0	0	0	0	1	有厅	3	222.79	7.6306
12823	1	0	0	0	0	0	0	0	1	有厅	4	205.17	9.7481
8868	1	0	0	0	0	0	1	0	1	有厅	2	61.15	6.5413
6253	1	0	0	0	0	0	0	1	1	有厅	2	122.00	5.4919
1041	1	0	0	0	0	0	1	0	1	无厅	1	62.00	4.5162
2537	1	0	0	0	0	1	0	1	1	有厅	3	173.12	4.9099
13043	1	0	0	0	0	1	0	1	1	有厅	1	72.88	8.1916
12641	1	0	0	0	0	0	0	1	1	有厅	1	57.00	8.2457
144	1	0	0	0	0	0	0	0	1	有厅	3	88.00	7.0455
6339	1	0	0	0	0	0	1	0	1	有厅	2	56.00	6.0715
7711	1	0	0	0	0	0	0	1	1	有厅	2	75.18	7.7149
5929	1	0	0	0	0	0	0	1	1	有厅	3	63.09	10.1443
5142	1	0	0	0	0	0	1	1	1	有厅	2	108.50	8.0185
...	...	...	...	...	...	...	...	...	...	...	...	...	...
14547	0	0	0	0	1	0	0	1	1	有厅	2	60.40	8.7749
3494	0	0	0	0	1	1	0	1	1	有厅	5	77.30	9.7025
14197	0	0	0	0	1	0	0	1	0	有厅	3	66.00	7.5000
58	0	0	0	0	1	0	0	1	1	有厅	2	57.70	10.4853
8884	0	0	0	0	1	0	1	1	1	有厅	2	58.10	8.6059
11702	0	0	0	0	1	1	0	0	1	有厅	2	50.07	7.4296
14600	0	0	0	0	1	1	0	1	1	有厅	2	64.00	9.8438
3834	0	0	0	0	1	0	1	0	1	有厅	1	56.00	8.0358
7524	0	0	0	0	1	0	0	1	1	有厅	3	56.80	10.8275
3534	0	0	0	0	1	1	0	1	1	有厅	2	66.60	10.4355
2181	0	0	0	0	1	1	0	1	1	有厅	3	65.60	11.0061
1796	0	0	0	0	1	1	0	1	1	有厅	2	56.75	7.3128
6512	0	0	0	0	1	0	1	1	1	有厅	2	115.33	7.5003
12787	0	0	0	0	1	0	0	1	0	有厅	1	54.56	11.1254
14631	0	0	0	0	1	0	1	1	1	有厅	2	70.10	9.2012
14544	0	0	0	0	1	0	1	1	1	有厅	2	83.30	8.9436
13093	0	0	0	0	1	0	0	1	1	有厅	3	66.47	8.8010
5427	0	0	0	0	1	0	0	0	1	有厅	4	299.00	4.3479
8652	0	0	0	0	1	0	0	0	1	有厅	2	81.37	6.8822
8247	0	0	0	0	1	0	0	1	1	有厅	1	44.70	8.1880
9104	0	0	0	0	1	1	0	1	1	有厅	4	162.77	5.5293
6260	0	0	0	0	1	1	0	1	1	有厅	3	198.00	8.8384
6839	0	0	0	0	1	1	0	0	1	有厅	3	141.31	9.3837
3300	0	0	0	0	1	1	0	1	1	有厅	2	66.30	14.4797
10680	0	0	0	0	1	0	1	1	1	有厅	2	82.78	10.2682
9519	0	0	0	0	1	0	1	0	1	有厅	4	165.00	10.0000
10862	0	0	0	0	1	0	1	0	1	有厅	2	79.52	6.2878
12889	0	0	0	0	1	0	0	0	1	有厅	2	100.92	7.4317
14487	0	0	0	0	1	1	0	1	1	有厅	2	71.30	10.2104
4264	0	0	0	0	1	0	0	1	1	有厅	3	143.05	7.6897

2400 rows × 13 columns

#法一：分步法，结合上面的步骤，自己生成哑变量
#lm1 = ols("price ~ dist_丰台+dist_朝阳+dist_东城+dist_海淀+dist_西城+school+subway+floor_middle+floor_low+style_new+roomnum+AREA", data=dat1).fit()
lm1 = ols("price ~ dist_丰台+dist_朝阳+dist_东城+dist_海淀+dist_西城+school+subway+floor_middle+floor_low+AREA", data=dat1).fit()
lm1_summary = lm1.summary()
lm1_summary  #回归结果展示

OLS Regression Results
Dep. Variable:	price	R-squared:	0.612
Model:	OLS	Adj. R-squared:	0.611
Method:	Least Squares	F-statistic:	377.5
Date:	Sun, 02 Feb 2020	Prob (F-statistic):	0.00
Time:	13:54:37	Log-Likelihood:	-4203.5
No. Observations:	2400	AIC:	8429.
Df Residuals:	2389	BIC:	8493.
Df Model:	10
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	3.6481	0.109	33.599	0.000	3.435	3.861
dist_丰台	0.0920	0.100	0.921	0.357	-0.104	0.288
dist_朝阳	0.8572	0.103	8.303	0.000	0.655	1.060
dist_东城	2.4669	0.107	23.097	0.000	2.257	2.676
dist_海淀	2.2663	0.105	21.518	0.000	2.060	2.473
dist_西城	3.6218	0.109	33.358	0.000	3.409	3.835
school	1.2521	0.073	17.192	0.000	1.109	1.395
subway	0.6251	0.078	8.036	0.000	0.473	0.778
floor_middle	0.1325	0.069	1.928	0.054	-0.002	0.267
floor_low	0.2720	0.070	3.867	0.000	0.134	0.410
AREA	-0.0016	0.001	-2.407	0.016	-0.003	-0.000

Omnibus:	177.616	Durbin-Watson:	2.012
Prob(Omnibus):	0.000	Jarque-Bera (JB):	294.765
Skew:	0.556	Prob(JB):	9.83e-65
Kurtosis:	4.309	Cond. No.	679.

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

#法二：自动生成哑变量
lm1 = ols("price ~ C(dist)+school+subway+C(floor)+AREA", data=dat01).fit()
lm1_summary = lm1.summary()
lm1_summary  #回归结果展示

OLS Regression Results
Dep. Variable:	price	R-squared:	0.605
Model:	OLS	Adj. R-squared:	0.603
Method:	Least Squares	F-statistic:	365.9
Date:	Sun, 02 Feb 2020	Prob (F-statistic):	0.00
Time:	13:41:14	Log-Likelihood:	-4241.8
No. Observations:	2400	AIC:	8506.
Df Residuals:	2389	BIC:	8569.
Df Model:	10
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	6.0100	0.131	45.909	0.000	5.753	6.267
C(dist)[T.丰台]	-2.2780	0.106	-21.551	0.000	-2.485	-2.071
C(dist)[T.朝阳]	-1.4887	0.103	-14.462	0.000	-1.691	-1.287
C(dist)[T.海淀]	-0.2538	0.101	-2.501	0.012	-0.453	-0.055
C(dist)[T.石景山]	-2.5005	0.108	-23.056	0.000	-2.713	-2.288
C(dist)[T.西城]	1.4003	0.101	13.862	0.000	1.202	1.598
C(floor)[T.low]	0.1864	0.072	2.574	0.010	0.044	0.328
C(floor)[T.middle]	0.0293	0.070	0.420	0.675	-0.108	0.166
school	1.1267	0.073	15.391	0.000	0.983	1.270
subway	0.6695	0.078	8.541	0.000	0.516	0.823
AREA	-0.0008	0.001	-1.158	0.247	-0.002	0.001

Omnibus:	210.844	Durbin-Watson:	1.942
Prob(Omnibus):	0.000	Jarque-Bera (JB):	360.176
Skew:	0.626	Prob(JB):	6.15e-79
Kurtosis:	4.426	Cond. No.	710.

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

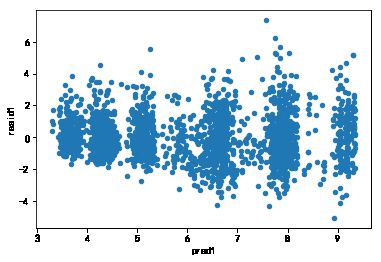
dat1['pred1']=lm1.predict(dat1)
dat1['resid1']=lm1.resid
dat1.plot('pred1','resid1',kind='scatter')  #模型诊断图，存在异方差现象，对因变量取对数

4、对数线性模型

###对数线性模型
dat1['price_ln'] = np.log(dat1['price'])  #对price取对数
dat1['AREA_ln'] = np.log(dat1['AREA'])#对AREA取对数

#面积未取对数
lm2 = ols("price_ln ~ dist_丰台+dist_朝阳+dist_东城+dist_海淀+dist_西城+school+subway+floor_middle+floor_low+AREA", data=dat1).fit()
lm2_summary = lm2.summary()
lm2_summary  #回归结果展示

OLS Regression Results
Dep. Variable:	price_ln	R-squared:	0.628
Model:	OLS	Adj. R-squared:	0.627
Method:	Least Squares	F-statistic:	403.6
Date:	Sun, 02 Feb 2020	Prob (F-statistic):	0.00
Time:	13:58:38	Log-Likelihood:	180.47
No. Observations:	2400	AIC:	-338.9
Df Residuals:	2389	BIC:	-275.3
Df Model:	10
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	1.2872	0.017	73.654	0.000	1.253	1.321
dist_丰台	0.0361	0.016	2.245	0.025	0.005	0.068
dist_朝阳	0.2026	0.017	12.190	0.000	0.170	0.235
dist_东城	0.4606	0.017	26.793	0.000	0.427	0.494
dist_海淀	0.4408	0.017	26.003	0.000	0.408	0.474
dist_西城	0.6169	0.017	35.301	0.000	0.583	0.651
school	0.1779	0.012	15.176	0.000	0.155	0.201
subway	0.1206	0.013	9.630	0.000	0.096	0.145
floor_middle	0.0258	0.011	2.328	0.020	0.004	0.047
floor_low	0.0499	0.011	4.410	0.000	0.028	0.072
AREA	-0.0002	0.000	-2.113	0.035	-0.000	-1.62e-05

Omnibus:	15.330	Durbin-Watson:	1.990
Prob(Omnibus):	0.000	Jarque-Bera (JB):	21.184
Skew:	-0.049	Prob(JB):	2.51e-05
Kurtosis:	3.450	Cond. No.	679.

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

#面积价格均取对数
lm2 = ols("price_ln ~ dist_丰台+dist_朝阳+dist_东城+dist_海淀+dist_西城+school+subway+floor_middle+floor_low+AREA_ln", data=dat1).fit()
lm2_summary = lm2.summary()
lm2_summary  #回归结果展示

OLS Regression Results
Dep. Variable:	price_ln	R-squared:	0.629
Model:	OLS	Adj. R-squared:	0.627
Method:	Least Squares	F-statistic:	404.3
Date:	Sun, 02 Feb 2020	Prob (F-statistic):	0.00
Time:	13:58:45	Log-Likelihood:	181.65
No. Observations:	2400	AIC:	-341.3
Df Residuals:	2389	BIC:	-277.7
Df Model:	10
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	1.3926	0.050	27.805	0.000	1.294	1.491
dist_丰台	0.0375	0.016	2.332	0.020	0.006	0.069
dist_朝阳	0.2040	0.017	12.287	0.000	0.171	0.237
dist_东城	0.4606	0.017	26.852	0.000	0.427	0.494
dist_海淀	0.4414	0.017	26.056	0.000	0.408	0.475
dist_西城	0.6164	0.017	35.309	0.000	0.582	0.651
school	0.1782	0.012	15.210	0.000	0.155	0.201
subway	0.1199	0.013	9.580	0.000	0.095	0.144
floor_middle	0.0258	0.011	2.329	0.020	0.004	0.047
floor_low	0.0501	0.011	4.424	0.000	0.028	0.072
AREA_ln	-0.0286	0.011	-2.613	0.009	-0.050	-0.007

Omnibus:	15.051	Durbin-Watson:	1.989
Prob(Omnibus):	0.001	Jarque-Bera (JB):	20.817
Skew:	-0.045	Prob(JB):	3.02e-05
Kurtosis:	3.447	Cond. No.	52.1

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

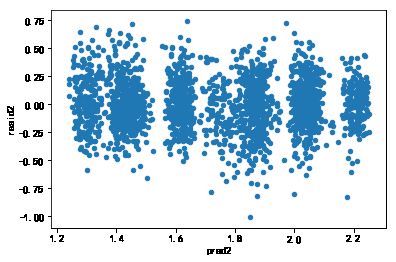
dat1['pred2']=lm2.predict(dat1)
dat1['resid2']=lm2.resid
dat1.plot('pred2','resid2',kind='scatter')  #模型诊断图，异方差现象得到消除

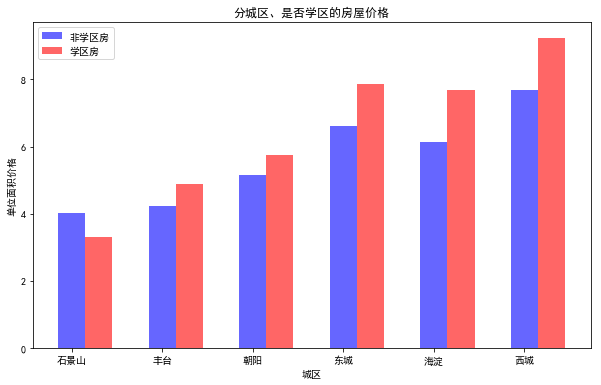
5、有交互项的对数线性模型，城区和学区之间的交互作用

重要变量间的交互性需要考虑

###交互作用的解释
schools=['丰台','朝阳','东城','海淀','西城']
print('石景山非学区房\t',round(data0[(data0['dist']=='石景山')&(data0['school']==0)]['price'].mean(),2),'万元/平方米\t',
     '石景山学区房\t',round(data0[(data0['dist']=='石景山')&(data0['school']==1)]['price'].mean(),2),'万元/平方米')
print('-------------------------------------------------------------------------')
for i in schools:
    print(i+'非学区房\t',round(dat1[(dat1['dist_'+i]==1)&(dat1['school']==0)]['price'].mean(),2),'万元/平方米\t',i+'学区房\t',round(dat1[(dat1['dist_'+i]==1)&(dat1['school']==1)]['price'].mean(),2),'万元/平方米')

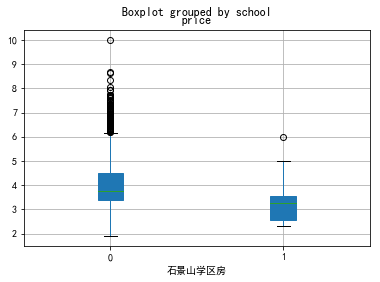
石景山非学区房	 4.04 万元/平方米	 石景山学区房	 3.31 万元/平方米
-------------------------------------------------------------------------
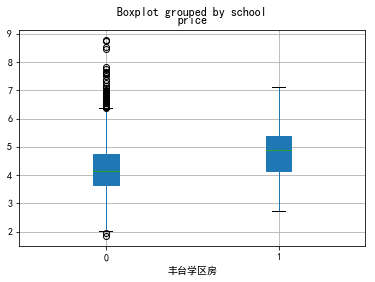
丰台非学区房	 4.2 万元/平方米	 丰台学区房	 5.16 万元/平方米
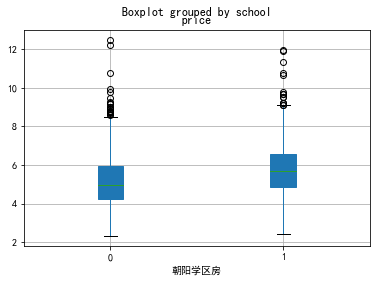
朝阳非学区房	 5.19 万元/平方米	 朝阳学区房	 5.6 万元/平方米
东城非学区房	 6.62 万元/平方米	 东城学区房	 8.03 万元/平方米
海淀非学区房	 6.26 万元/平方米	 海淀学区房	 7.8 万元/平方米
西城非学区房	 7.63 万元/平方米	 西城学区房	 9.2 万元/平方米

###探索石景山学区房价格比较低的原因，是否是样本量的问题？
print('石景山非学区房\t',data0[(data0['dist']=='石景山')&(data0['school']==0)].shape[0],'\t',
     '石景山学区房\t',data0[(data0['dist']=='石景山')&(data0['school']==1)].shape[0],'\t','石景山学区房仅占石景山所有二手房的0.92%')

石景山非学区房	 1929 	 石景山学区房	 18 	 石景山学区房仅占石景山所有二手房的0.92%

###构造图形揭示不同城区是否学区房的价格问题
df=pd.DataFrame()
dist=['石景山','丰台','朝阳','东城','海淀','西城']
Noschool=[]
school=[]
for i in dist:
    Noschool.append(data0[(data0['dist']==i)&(data0['school']==0)]['price'].mean())
    school.append(data0[(data0['dist']==i)&(data0['school']==1)]['price'].mean())

df['dist']=pd.Series(dist)
df['Noschool']=pd.Series(Noschool)
df['school']=pd.Series(school)
df

	dist	Noschool	school
0	石景山	4.035388	3.310733
1	丰台	4.229100	4.887162
2	朝阳	5.158851	5.740341
3	东城	6.627689	7.851490
4	海淀	6.138580	7.691126
5	西城	7.698937	9.246887

df1=df['Noschool'].T.values
df2=df['school'].T.values
plt.figure(figsize=(10,6))
x1=range(0,len(df))
x2=[i+0.3 for i in x1]
plt.bar(x1,df1,color='b',width=0.3,alpha=0.6,label='非学区房')
plt.bar(x2,df2,color='r',width=0.3,alpha=0.6,label='学区房')
plt.xlabel('城区')
plt.ylabel('单位面积价格')
plt.title('分城区、是否学区的房屋价格')
plt.legend(loc='upper left')
plt.xticks(range(0,6),dist)
plt.show()

###分城区的学区房分组箱线图
school=['石景山','丰台','朝阳','东城','海淀','西城']
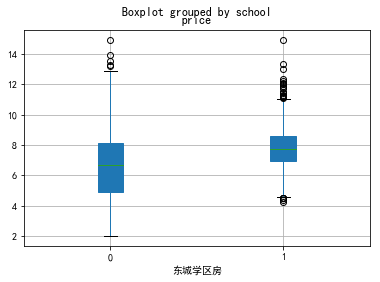
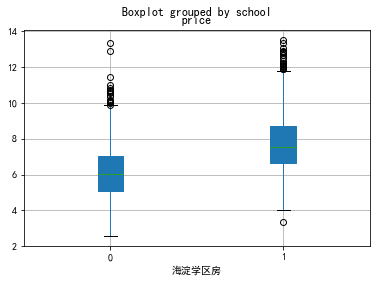
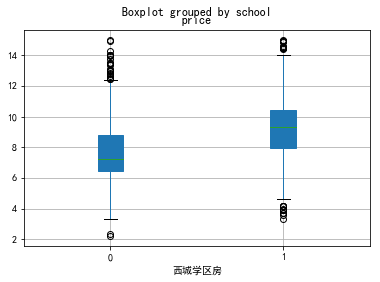
for i in school:
    data0[data0.dist==i][['school','price']].boxplot(by='school',patch_artist=True)
    plt.xlabel(i+'学区房')

###有交互项的对数线性模型，城区和学区之间的交互作用
lm3 = ols("price_ln ~ (dist_丰台+dist_朝阳+dist_东城+dist_海淀+dist_西城)*school+subway+floor_middle+floor_low+AREA_ln", data=dat1).fit()
lm3_summary = lm3.summary()
lm3_summary  #回归结果展示

OLS Regression Results
Dep. Variable:	price_ln	R-squared:	0.633
Model:	OLS	Adj. R-squared:	0.631
Method:	Least Squares	F-statistic:	274.7
Date:	Sun, 02 Feb 2020	Prob (F-statistic):	0.00
Time:	14:03:01	Log-Likelihood:	197.64
No. Observations:	2400	AIC:	-363.3
Df Residuals:	2384	BIC:	-270.8
Df Model:	15
Covariance Type:	nonrobust

	coef	std err	t	P>\|t\|	[0.025	0.975]
Intercept	1.3932	0.050	27.869	0.000	1.295	1.491
dist_丰台	0.0347	0.016	2.148	0.032	0.003	0.066
dist_朝阳	0.2206	0.017	12.785	0.000	0.187	0.254
dist_东城	0.4436	0.019	23.103	0.000	0.406	0.481
dist_海淀	0.4247	0.019	22.289	0.000	0.387	0.462
dist_西城	0.6076	0.021	29.272	0.000	0.567	0.648
school	-0.4513	0.159	-2.843	0.005	-0.763	-0.140
dist_丰台:school	0.6332	0.172	3.683	0.000	0.296	0.970
dist_朝阳:school	0.5311	0.161	3.293	0.001	0.215	0.847
dist_东城:school	0.6634	0.160	4.137	0.000	0.349	0.978
dist_海淀:school	0.6595	0.160	4.110	0.000	0.345	0.974
dist_西城:school	0.6411	0.160	3.997	0.000	0.327	0.956
subway	0.1152	0.012	9.217	0.000	0.091	0.140
floor_middle	0.0261	0.011	2.372	0.018	0.005	0.048
floor_low	0.0513	0.011	4.558	0.000	0.029	0.073
AREA_ln	-0.0274	0.011	-2.511	0.012	-0.049	-0.006

Omnibus:	10.682	Durbin-Watson:	1.991
Prob(Omnibus):	0.005	Jarque-Bera (JB):	14.045
Skew:	-0.015	Prob(JB):	0.000892
Kurtosis:	3.374	Cond. No.	399.

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

###假想情形，做预测，x_new是新的自变量
x_new1=dat1.head(1)
x_new1

	dist_东城	dist_丰台	dist_朝阳	dist_海淀	dist_西城	floor_low	floor_middle	school	subway	style_new	roomnum	AREA	price	pred1	resid1	price_ln	AREA_ln	pred2	resid2
1014	1	0	0	0	0	1	0	1	1	有厅	2	69.64	8.6876	8.153592	0.534008	2.161897	4.248495	2.079982	0.081767

x_new1['dist_朝阳']=0

x_new1['dist_东城']=1
x_new1['roomnum']=2
x_new1['halls']=1
x_new1['AREA_ln']=np.log(70)
x_new1['subway']=1
x_new1['school']=1
x_new1['style_new']="有厅"
x_new1

	dist_东城	dist_丰台	dist_朝阳	dist_海淀	dist_西城	floor_low	floor_middle	school	subway	style_new	roomnum	AREA	price	pred1	resid1	price_ln	AREA_ln	pred2	resid2	halls
1014	1	0	0	0	0	1	0	1	1	有厅	2	69.64	8.6876	8.153592	0.534008	2.161897	4.248495	2.079982	0.081767	1

#预测值
print("单位面积房价：",round(math.exp(lm3.predict(x_new1)),2),"万元/平方米")
print("总价：",round(math.exp(lm3.predict(x_new1))*70,2),"万元")

单位面积房价： 8.16 万元/平方米
总价： 571.1 万元

你可能感兴趣的:(#,数据科学,案例篇,python数据挖掘)

那个抄袭的大张伟猫小努
最近一直在追《即刻电音》这个综艺，除了觉得出场节目的音乐制作人有意思之外，也觉得有两个导师挺有趣的（另外一个就忽略了吧）。孙艺兴在上一篇文章里面已经说过了，那么这篇就说说我们的大老师，大张伟吧。其实在节目刚开始大张伟出来的时候，我以为他是属于导师里面来活跃气氛负责搞笑的，毕竟孙艺兴属于卖萌卖傻卖老实的，尚雯婕一般负责装逼耍狠的，而大张伟一贯以来上综艺的形象基本上都是蹦蹦跳跳带动气氛的。谁知道，两期
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
腾讯云技术深度探索：构建高效云原生微服务架构我的运维人生云原生架构腾讯云运维开发技术共享
腾讯云技术深度探索：构建高效云原生微服务架构在当今快速发展的技术环境中，云原生技术已成为企业数字化转型的关键驱动力。腾讯云作为行业领先的云服务提供商，不断推出创新的产品和技术，助力企业构建高效、可扩展的云原生微服务架构。本文将深入探讨腾讯云在微服务领域的最新进展，并通过一个实际案例展示如何在腾讯云平台上构建云原生应用。腾讯云微服务架构概览腾讯云微服务架构基于云原生理念，旨在帮助企业快速实现应用的容
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
18-115 一切思考不能有效转化为行动，都TM是扯淡！成长时间线
7月25号写了一篇关于为什么会断更如此严重的反思，然而，之后日更仅仅维持了一周，又出现了这次更严重的现象。从8月2号到昨天8月6号，5天！又是5天没有更文！虽然这次断更时间和上次一样，那为什么说这次更严重？因为上次之后就分析了问题的原因，以及应该如何解决，按理说应该会好转，然而，没过几天严重断更的现象再次出现，想想，经过反思，问题依然没有解决与改变，这让我有些担忧。到底是哪里出了问题，难道我就真的
直返最高等级与直返APP：无需邀请码的返利新体验古楼
随着互联网的普及和电商的兴起，直返模式逐渐成为一种流行的商业模式。在这种模式下，消费者通过购买产品或服务，获得一定的返利，并可以分享给更多的人。其中，直返最高等级和直返APP是直返模式中的重要概念和工具。本文将详细介绍直返最高等级的概念、直返APP的使用以及与邀请码的关系。【高省】APP（高佣金领导者）是一个自用省钱佣金高，分享推广赚钱多的平台，百度有几百万篇报道，运行三年，稳定可靠。高省APP，
高端密码学院笔记285 柚子_b4b4
高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
想明白这个问题，你才能写下去文自拾
春节放假的时候，又有一天梦见她，第二天她冒着漫天大雪，傻傻地跑来见我。她说，见见傻傻的我，天很冷，心很暖。她回去后，我写了一篇文章，题目叫——从此梦中只有你。我们没在一起的很长一段时间里，她都在我的心底，一次次出现在我的梦里。我对她说，在一起之前，是胆小且闷骚，在一起之后，我变得不要脸了。不要脸的——去爱你。那文章没写完，火车上，给她看了。我有点小失望，花了好几个小时写，她分分钟就看完，很希望她逐
Kafka 消息丢失如何处理？架构文摘JGWZ 学习
今天给大家分享一个在面试中经常遇到的问题：Kafka消息丢失该如何处理？这个问题啊，看似简单，其实里面藏着很多“套路”。来，咱们先讲一个面试的“真实”案例。面试官问：“Kafka消息丢失如何处理？”小明一听，反问：“你是怎么发现消息丢失了？”面试官顿时一愣，沉默了片刻后，可能有点不耐烦，说道：“这个你不用管，反正现在发现消息丢失了，你就说如何处理。”小明一头雾水：“问题是都不知道怎么丢的，处理起来
2022现在哪个打车软件比较好用又便宜实惠的打车软件合集高省APP珊珊
这是一个信息高速传播的社会。信息可以通过手机，微信，自媒体，抖音等方式进行传播。但同时这也是一个交通四通发达的社会。高省APP，是2022年推出的平台，0投资，0风险、高省APP佣金更高，模式更好，终端用户不流失。【高省】是一个自用省钱佣金高，分享推广赚钱多的平台，百度有几百万篇报道，也期待你的加入。珊珊导师，高省邀请码777777，注册送2皇冠会员，送万元推广大礼包，教你如何1年做到百万团队。高
走向以教育叙事为载体的教育叙事研究 666小飞鱼
今天我读了吴松超老师的《给教师的68条建写作建议》中的第23条《如何通过教育叙事走向研究》，吴老师在文中与我们分享了一个德育案例，这是一个反面的案例，意在告知我们在处理问题时，不能就考虑的点太窄，思考要全面。走向教育叙事研究，教师要有敏锐的“感知力”，这个感知力来自于背后专业知识的支撑，思维能力以及广阔的视野和见识等。所以对于同一件事处理方法不同，这个就是教师背后“敏锐力”的不同造成的，也就是说是
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
Redis系列：Geo 类型赋能亿级地图位置计算 Ly768768 redis bootstrap 数据库
1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构，它是基于不同业务场景而设计的：动态字符串(REDIS_STRING)：整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
2019-11-04复盘——飞来山上千寻塔，闻说鸡鸣见日升。那一叶秋
1、大盘篇先上老图，看习惯了，也就知道走势了图1上证指数日线图还是那张老图，自己可以在自己的相关软件上画出来，快变盘了。2、个股篇未加仓、未减仓。分析量能的时候，突然发现这么一个东西：“放量突破年线，缩量回调。”合众科技日线图其实，最近的N只个股，在技术分析上，都到了变盘的临界时候。结合这么久的走势，特别是ZJH不断放开IPO的申请，本质上说是融资难度变大，或者说是为企业的融资开创便利。但现在市场
18、架构-可观测性之聚合度量大树~~ 架构 java python 后端架构
聚合度量聚合度量是指对系统运行时产生的各种指标数据进行收集、聚合和分析，以了解系统的健康状况和性能表现。聚合度量是可观测性的关键组成部分，通过对度量数据的分析，可以及时发现系统中的异常和瓶颈。以下是对聚合度量各个方面的详细解析，并结合具体的数据案例和技术支撑。指标收集收集系统运行时产生的各种指标数据是聚合度量的基础。常见的指标包括CPU使用率、内存使用率、请求处理时间、请求数、错误率等。以下是指标
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
【六】阿伟开始搭建Kafka学习环境能源恒观中间件学习 kafka spring
阿伟开始搭建Kafka学习环境概述上一篇文章阿伟学习了Kafka的核心概念，并且把市面上流行的消息中间件特性进行了梳理和对比，方便大家在学习过程中进行对比学习，最后梳理了一些Kafka使用中经常遇到的Kafka难题以及解决思路，经过上一篇的学习我相信大家对Kafka有了初步的认识，本篇将继续学习Kafka。一、安装和配置学习一项技术首先要搭建一套服务，而Kafka的运行主要需要部署jdk、zook
2022-08-28 蔚蓝一片晴
初三暑假培训收获点滴从8月25至8月27日三天两晚的培训结束了，回到家中，该静下心来整理一下触动心灵的收获，成为成长的积淀。1.在优秀团队中快速成长与提升，做一名反思成长型教师一名专业型教师的教学指导包括了教学原理知识、案例知识、策略知识。面对教学中的遇到的有趣的情形、问题会去研究其理，寻找更好的教法学法对策。从新手到成熟型教师，再走向专业型教师，需要的是觉醒与反思，多进行案例研究，从案例中观察、
多子女家庭问题 3e5c5362403c
杨宁宁焦点解决网络初17中19坚持分享589天（2021.3.20）本周约练我1次，总计166次，读书打卡第256天案例督导收获：【家有老大篇】被爱与高期待下的独舞家里的第一个孩子往往集万千宠爱于一身。爸爸妈妈、爷爷奶奶、姥姥姥爷的目光都聚焦在他的身上。在这种光环下长大的孩子，就如小皇帝一般，衣来伸手、饭来张口。拥有爱的同时，也意味着拥有了更高的被期待，父母会花血本给你报各种各样的早教班，给你买各
戴先华2021.4.18《我的第129篇幸运作业》 39f4298779c4
2021.4.18今天小宝和大表姐出去玩，我和婆婆在烧饭，突然小宝冲了进来，告诉奶奶说：“奶奶，奶奶姐姐在亭子里倒了”我一下子看出小宝的紧张，马上跑了出去，发现大外甥女又患了病，看起来心疼极了，整个人面朝地下的倒下了，在地上不停的抽搐，额头摔了一个大泡，整张脸都是紫色的，眼睛边上都出血了，真的是非常紧张，这么多年姐姐两夫妻就这样看着自己的孩子一次次晕倒，姐夫这么多年，年年都拿不出钱回家，使得家一次
我与《红楼梦》‖纪念曹雪芹出生307周年！归海逸舟是周成功子阳佳乐归海逸舟是周成功子阳佳乐
【今日作家推荐】中国古典小说之首《红楼梦》，其作者曹雪芹是文坛泰斗。约1715年5月28日，曹雪芹出生。所以，今天推荐的是中国人众所周知的作家——曹雪芹。曹雪芹在世界读者心目中也影响广大，可以与西方世界引以为豪的莎士比亚、歌德等媲美。1、我与《红楼梦》我一直想写一篇和《红楼梦》相关的文章，现在机会终于来了！《红楼梦》作为我国家喻户晓的文学名著，其影响是空前的。还在我很小的时候，姥姥经常讲《红楼梦》
白骑士的Java教学基础篇 2.5 控制流语句白骑士所长 Java 教学 java 开发语言
欢迎继续学习Java编程的基础篇！在前面的章节中，我们了解了Java的变量、数据类型和运算符。接下来，我们将探讨Java中的控制流语句。控制流语句用于控制程序的执行顺序，使我们能够根据特定条件执行不同的代码块，或重复执行某段代码。这是编写复杂程序的基础。通过学习这一节内容，你将掌握如何使用条件语句和循环语句来编写更加灵活和高效的代码。条件语句条件语句用于根据条件的真假来执行不同的代码块。if语句‘
第二十 python基础--语句九樱MOL
目录具体内容1：if语句的使用格式判断语句2：if-else的使用格式3：if-elif-else的使用格式4：if嵌套1：while循环的格式循环语句2：while循环嵌套3：for循环的格式一、判断语句在程序中如果某些条件满足，才能做某件事情，而不满足时不允许做，这就是所谓的判断1.1if语句的使用格式if要判断的条件:条件成立时，要做的事情案例:判断年纪，如果age大于18，输入成年age=
系统架构设计师需求分析篇二 AmHardy 软件架构设计师系统架构需求分析面向对象分析分析模型 UML和SysML
面向对象分析方法1.用例模型构建用例模型一般需要经历4个阶段：识别参与者：识别与系统交互的所有事物。合并需求获得用例：将需求分配给予其相关的参与者。细化用例描述：详细描述每个用例的功能。调整用例模型：优化用例之间的关系和结构，前三个阶段是必需的。2.用例图的三元素参与者：使用系统的用户或其他外部系统和设备。用例：系统所提供的服务。通信关联：参与者和用例之间的关系，或用例与用例之间的关系。3.识别参
手机上有什么兼职可以做？网上兼职一单一结手机就可以做？优惠券高省
建议上班族和全职宝妈把空闲时间拿出来一点做做副业，什么也不耽搁还能多一笔收入！推荐大家一定要试一试！！！只要有手机就可以做，下面小编就为大家推荐用手机就可以做的三类网上兼职工作。一，高省APP高省APP佣金更高，模式更好，终端用户不流失。【高省】是一个自用省钱佣金高，分享推广赚钱多的平台，百度有几百万篇报道，也期待你的加入。万方导师高省邀请码005500，注册送双皇冠会员，送万元推广大礼包，教你如
2023-06-19【感恩日记】第246篇 o泡沫o
思想日记：坚持下去，相信自己一定可以的【感恩日记】第246篇1.我真是太幸福啦！感恩孩子早起阅读，放学到学生之家完成作业，平安度过美好的一天。感恩！感恩！感恩！❤️2.我真是太幸福啦！感恩自己早起给孩子煮早餐，完成计划的工作，晚上学习。感恩！感恩！感恩！❤️3.我真是太幸福啦！感恩为我设计效果图的老师。感恩！感恩！感恩！❤️4.我真是太幸福啦！感恩父母养育了我，有妈的孩子真幸福。感恩！感恩！感恩！
摄影小白，怎么才能拍出高大上产品图片？是波妞唉
很多人以为文案只要会码字，会排版就OK了！说实话，没接触到这一行的时候，我的想法更简单，以为只要会写字就行！可是真做了文案才发现，码字只是入门级的基本功。一篇文章离不开排版、配图，说起来很简单！从头做到尾你就会发现，写文章用两个小时，找合适的配图居然要花掉半天的时间，甚至更久！图片能找到合适的就不怕，还有找不到的，比如产品图，只能亲自拍。拿着摆弄了半天，就是拍不出想要的效果，光线不好、搭出来丑破天
Spring MVC 全面指南：从入门到精通的详细解析一杯梅子酱技术栈学习 spring mvc java
引言：SpringMVC，作为Spring框架的一个重要模块，为构建Web应用提供了强大的功能和灵活性。无论是初学者还是有一定经验的开发者，掌握SpringMVC都将显著提升你的Web开发技能。本文旨在为初学者提供一个全面且易于理解的学习路径，通过详细的知识点分析和实际案例，帮助你快速上手SpringMVC，让学习过程既深刻又高效。一、SpringMVC简介1.1什么是SpringMVC？Spri
【创客文案社】第三期写手招募筱瑶123
创客文案社第三期写手招募开始了。要求：1：注册一个月以上2：本身热爱写作3：有时间参与接单投稿参与方式：可以关注公众号：写作灵感；也可以通过其他转发文章的文友帮忙拉入群；也可以简信我。参与之后的文友，会先进入新人班，进行基本的试稿与培训，先接一些比较简单的单子；在这里可以一边赚钱，一边学习。不知不觉，来三四个月了，也发现了很多很有意思的现象。1：在上写一篇文章，基本都是几毛钱，多的也不过几块钱的收
LeetCode[Math] - #66 Plus One Cwind java LeetCode 题解 Algorithm Math
原题链接：#66 Plus One 要求：给定一个用数字数组表示的非负整数，如num1 = {1, 2, 3, 9}, num2 = {9, 9}等，给这个数加上1。注意： 1. 数字的较高位存在数组的头上，即num1表示数字1239 2. 每一位（数组中的每个元素）的取值范围为0~9 难度：简单分析：题目比较简单，只须从数组
JQuery中$.ajax()方法参数详解 AILIKES JavaScript jsonp jquery Ajax json
url: 要求为String类型的参数，（默认为当前页地址）发送请求的地址。 type: 要求为String类型的参数，请求方式（post或get）默认为get。注意其他http请求方法，例如put和 delete也可以使用，但仅部分浏览器支持。 timeout: 要求为Number类型的参数，设置请求超时时间（毫秒）。此设置将覆盖$.ajaxSetup()方法的全局
JConsole & JVisualVM远程监视Webphere服务器JVM Kai_Ge JVisualVM JConsole Webphere
JConsole是JDK里自带的一个工具，可以监测Java程序运行时所有对象的申请、释放等动作，将内存管理的所有信息进行统计、分析、可视化。我们可以根据这些信息判断程序是否有内存泄漏问题。　　使用JConsole工具来分析WAS的JVM问题，需要进行相关的配置。　　首先我们看WAS服务器端的配置. 　　1、登录was控制台https://10.4.119.18
自定义annotation 120153216 annotation
Java annotation 自定义注释@interface的用法一、什么是注释说起注释，得先提一提什么是元数据(metadata)。所谓元数据就是数据的数据。也就是说，元数据是描述数据的。就象数据表中的字段一样，每个字段描述了这个字段下的数据的含义。而J2SE5.0中提供的注释就是java源代码的元数据，也就是说注释是描述java源
CentOS 5/6.X 使用 EPEL YUM源 2002wmj centos
CentOS 6.X 安装使用EPEL YUM源1. 查看操作系统版本[root@node1 ~]# uname -a Linux node1.test.com 2.6.32-358.el6.x86_64 #1 SMP Fri Feb 22 00:31:26 UTC 2013 x86_64 x86_64 x86_64 GNU/Linux [root@node1 ~]#
在SQLSERVER中查找缺失和无用的索引SQL 357029540 SQL Server
--缺失的索引 SELECT avg_total_user_cost * avg_user_impact * ( user_scans + user_seeks ) AS PossibleImprovement , last_user_seek ,
Spring3 MVC 笔记（二） —json+rest优化 7454103 Spring3 MVC
接上次的 spring mvc 注解的一些详细信息！其实也是一些个人的学习笔记呵呵！
替换“\”的时候报错Unexpected internal error near index 1 \ ^ adminjun java “\替换”
发现还是有些东西没有刻子脑子里,,过段时间就没什么概念了,所以贴出来...以免再忘... 在拆分字符串时遇到通过 \ 来拆分，可是用所以想通过转义 \\ 来拆分的时候会报异常 public class Main { /*
POJ 1035 Spell checker(哈希表) aijuans 暴力求解--哈希表
/* 题意：输入字典，然后输入单词，判断字典中是否出现过该单词，或者是否进行删除、添加、替换操作，如果是，则输出对应的字典中的单词要求按照输入时候的排名输出题解：建立两个哈希表。一个存储字典和输入字典中单词的排名，一个进行最后输出的判重 */ #include <iostream> //#define using namespace std; const int HASH =
通过原型实现javascript Array的去重、最大值和最小值 ayaoxinchao JavaScript array prototype
用原型函数（prototype）可以定义一些很方便的自定义函数，实现各种自定义功能。本次主要是实现了Array的去重、获取最大值和最小值。实现代码如下： <script type="text/javascript"> Array.prototype.unique = function() { var a = {}; var le
UIWebView实现https双向认证请求 bewithme UIWebView https Objective-C
什么是HTTPS双向认证我已在先前的博文 ASIHTTPRequest实现https双向认证请求中有讲述，不理解的读者可以先复习一下。本文是用UIWebView来实现对需要客户端证书验证的服务请求，网上有些文章中有涉及到此内容，但都只言片语，没有讲完全，更没有完整的代码，让人困扰不已。但是此知
NoSQL数据库之Redis数据库管理(Redis高级应用之事务处理、持久化操作、pub_sub、虚拟内存) bijian1013 redis 数据库 NoSQL
3.事务处理 Redis对事务的支持目前不比较简单。Redis只能保证一个client发起的事务中的命令可以连续的执行，而中间不会插入其他client的命令。当一个client在一个连接中发出multi命令时，这个连接会进入一个事务上下文，该连接后续的命令不会立即执行，而是先放到一个队列中，当执行exec命令时，redis会顺序的执行队列中
各数据库分页sql备忘 bingyingao oracle sql 分页
ORACLE 下面这个效率很低 SELECT * FROM ( SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_FS_RETURN order by id desc) A ) WHERE RN <20; 下面这个效率很高 SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_
【Scala七】Scala核心一：函数 bit1129 scala
1. 如果函数体只有一行代码，则可以不用写{},比如 def print(x: Int) = println(x) 一行上的多条语句用分号隔开，则只有第一句属于方法体，例如 def printWithValue(x: Int) : String= println(x); "ABC" 上面的代码报错，因为，printWithValue的方法
了解GHC的factorial编译过程 bookjovi haskell
GHC相对其他主流语言的编译器或解释器还是比较复杂的，一部分原因是haskell本身的设计就不易于实现compiler，如lazy特性，static typed，类型推导等。关于GHC的内部实现有篇文章说的挺好，这里，文中在RTS一节中详细说了haskell的concurrent实现，里面提到了green thread，如果熟悉Go语言的话就会发现，ghc的concurrent实现和Go有点类
Java-Collections Framework学习与总结-LinkedHashMap BrokenDreams LinkedHashMap
前面总结了java.util.HashMap，了解了其内部由散列表实现，每个桶内是一个单向链表。那有没有双向链表的实现呢？双向链表的实现会具备什么特性呢？来看一下HashMap的一个子类——java.util.LinkedHashMap。
读《研磨设计模式》-代码笔记-抽象工厂模式-Abstract Factory bylijinnan abstract
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ package design.pattern; /* * Abstract Factory Pattern * 抽象工厂模式的目的是： * 通过在抽象工厂里面定义一组产品接口，方便地切换“产品簇” * 这些接口是相关或者相依赖的
压暗面部高光 cherishLC PS
方法一、压暗高光&重新着色当皮肤很油又使用闪光灯时，很容易在面部形成高光区域。下面讲一下我今天处理高光区域的心得：皮肤可以分为纹理和色彩两个属性。其中纹理主要由亮度通道（Lab模式的L通道）决定，色彩则由a、b通道确定。处理思路为在保持高光区域纹理的情况下，对高光区域着色。具体步骤为：降低高光区域的整体的亮度，再进行着色。如果想简化步骤，可以只进行着色（参看下面的步骤1
Java VisualVM监控远程JVM crabdave visualvm
Java VisualVM监控远程JVM JDK1.6开始自带的VisualVM就是不错的监控工具. 这个工具就在JAVA_HOME\bin\目录下的jvisualvm.exe, 双击这个文件就能看到界面通过JMX连接远程机器, 需要经过下面的配置: 1. 修改远程机器JDK配置文件 (我这里远程机器是linux).
Saiku去掉登录模块 daizj saiku 登录 olap BI
1、修改applicationContext-saiku-webapp.xml <security:intercept-url pattern="/rest/**" access="IS_AUTHENTICATED_ANONYMOUSLY" /> <security:intercept-url pattern=&qu
浅析 Flex中的Focus dsjt html Flex Flash
关键字：focus、 setFocus、 IFocusManager、KeyboardEvent 焦点、设置焦点、获得焦点、键盘事件一、无焦点的困扰——组件监听不到键盘事件原因：只有获得焦点的组件（确切说是InteractiveObject）才能监听到键盘事件的目标阶段；键盘事件（flash.events.KeyboardEvent）参与冒泡阶段，所以焦点组件的父项（以及它爸
Yii全局函数使用 dcj3sjt126com yii
由于YII致力于完美的整合第三方库，它并没有定义任何全局函数。yii中的每一个应用都需要全类别和对象范围。例如，Yii::app()->user;Yii::app()->params['name'];等等。我们可以自行设定全局函数，使得代码看起来更加简洁易用。(原文地址) 我们可以保存在globals.php在protected目录下。然后，在入口脚本index.php的，我们包括在
设计模式之单例模式二（解决无序写入的问题） come_for_dream 单例模式 volatile 乱序执行双重检验锁
在上篇文章中我们使用了双重检验锁的方式避免懒汉式单例模式下由于多线程造成的实例被多次创建的问题，但是因为由于JVM为了使得处理器内部的运算单元能充分利用，处理器可能会对输入代码进行乱序执行（Out Of Order Execute）优化，处理器会在计算之后将乱序执行的结果进行重组，保证该
程序员从初级到高级的蜕变 gcq511120594 框架工作 PHP android html5
软件开发是一个奇怪的行业，市场远远供不应求。这是一个已经存在多年的问题，而且随着时间的流逝，愈演愈烈。我们严重缺乏能够满足需求的人才。这个行业相当年轻。大多数软件项目是失败的。几乎所有的项目都会超出预算。我们解决问题的最佳指导方针可以归结为——“用一些通用方法去解决问题，当然这些方法常常不管用，于是，唯一能做的就是不断地尝试，逐个看看是否奏效”。现在我们把淫浸代码时间超过3年的开发人员称为
Reverse Linked List hcx2013 list
Reverse a singly linked list. /** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ p
Spring4.1新特性——数据库集成测试 jinnianshilongnian spring 4.1
目录 Spring4.1新特性——综述 Spring4.1新特性——Spring核心部分及其他 Spring4.1新特性——Spring缓存框架增强 Spring4.1新特性——异步调用和事件机制的异常处理 Spring4.1新特性——数据库集成测试脚本初始化 Spring4.1新特性——Spring MVC增强 Spring4.1新特性——页面自动化测试框架Spring MVC T
C# Ajax上传图片同时生成微缩图(附Demo) liyonghui160com
1.Ajax无刷新上传图片,详情请阅我的这篇文章。（jquery + c# ashx） 2.C#位图处理 System.Drawing。 3.最新demo支持IE7,IE8,Fir
Java list三种遍历方法性能比较 pda158 java
从c/c++语言转向java开发，学习java语言list遍历的三种方法，顺便测试各种遍历方法的性能，测试方法为在ArrayList中插入1千万条记录，然后遍历ArrayList，发现了一个奇怪的现象，测试代码例如以下： package com.hisense.tiger.list; import java.util.ArrayList; import java.util.Iterator;
300个涵盖IT各方面的免费资源（上）——商业与市场篇 shoothao seo 商业与市场 IT资源免费资源
A.网站模板+logo+服务器主机+发票生成 HTML5 UP:响应式的HTML5和CSS3网站模板。 Bootswatch:免费的Bootstrap主题。 Templated:收集了845个免费的CSS和HTML5网站模板。 Wordpress.org|Wordpress.com:可免费创建你的新网站。 Strikingly:关注领域中免费无限的移动优
localStorage、sessionStorage uule localStorage
W3School 例子 HTML5 提供了两种在客户端存储数据的新方法： localStorage - 没有时间限制的数据存储 sessionStorage - 针对一个 session 的数据存储之前，这些都是由 cookie 完成的。但是 cookie 不适合大量数据的存储，因为它们由每个对服务器的请求来传递，这使得 cookie 速度很慢而且效率也不

数据科学 案例4 线性回归之房价预测（代码）

数据科学 案例4 房价预测（代码）

Step1:描述性统计

1、简单预处理

2、因变量（price）

1）因变量直方图

2）查看因变量的均值、中位数和标准差等更多信息

3）查看因变量最高和最低的两条观测

2、自变量

1）整体来看（连续变量与分类变量分开）

2) 变量dist

3) roomnum

4) halls

5) floor

6) subway+school （stack2dim函数）

7) AREA

Steo2:建模

1、首先检验每个解释变量是否和被解释变量独立（get_sample（）函数）

3 线性回归模型

4、对数线性模型

5、有交互项的对数线性模型，城区和学区之间的交互作用

你可能感兴趣的:(#,数据科学,案例篇,python数据挖掘)

数据科学案例4 线性回归之房价预测（代码）

数据科学案例4 房价预测（代码）