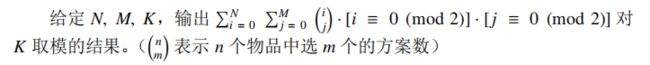jzoj6022 【GDOI2019模拟2019.2.15】求和 （组合数取模）

很常见的推式子套路，有个组合数取模的黑科技：

现在要求C(n,1),C(n,2)…C(n,m) (n<=1e9,m<=1e6)对一个大数p取模的结果，可以先将p分解质因数，然后将出现在p中的质因子单独计算指数以避免除法，其余的部分是与p互质的，直接使用逆元计算。（分解质因数时顺便求phi即可）
当只有乘除的时候就可以使用这种规避逆元的方法，计算一次乘除的复杂度是质因子个数的。
最后求值的时候，要预处理质因子的幂次。并且根据库默尔定理，C(n,m)中，任意质数p的幂次不会超过$lo{g}_{p}n$。所以预处理30个就可以了。

还记得在noip2016day2T1我也采用了这种方法，取得了70分的好成绩…

其余的部分就不是很普适了，看题解吧

#include 
#include 
#include 
#include 
using namespace std;
typedef long long ll;
const int N=1e6+100;
ll n,m,mo,ans;
ll s,t,C[N];
ll fac[20],phi,z[20][35],MO;
ll ksm(ll x,ll y,ll mo=MO){
	ll ret=1;for(;y;y>>=1){
		if(y&1)ret=ret*x%mo;
		x=x*x%mo;
	}
	return ret;
}
struct num{
	int e[20];
	ll v;
	ll mult(ll a,ll b){
		if (a==0){return v=0;}
		ll ret=1;
		for(int i=1;i<=fac[0];i++){
			int cnta=0,cntb=0;
			while(a%fac[i]==0)a/=fac[i],cnta++;
			while(b%fac[i]==0)b/=fac[i],cntb++;
			e[i]+=cnta-cntb;
			ret=ret*z[i][e[i]]%MO;
		}
		v=v*a%MO*ksm(b,phi-1)%MO;
		ret=ret*v%MO;
		return ret;
	}
}f[1000100];
void initC(ll mo,int d){
	MO=mo;
	ll tmp=mo;
	fac[0]=0;
	phi=1;
	for(int i=2;i*i<=tmp;i++)if(tmp%i==0){
		phi*=i-1;tmp/=i;
		while(tmp%i==0)tmp=tmp/i,phi*=i;
		fac[++fac[0]]=i;
		z[fac[0]][0]=1;
		for(int j=1;j<=30;j++)
			z[fac[0]][j]=z[fac[0]][j-1]*i%mo;
	}
	if(tmp!=1){
		fac[++fac[0]]=tmp,phi*=tmp-1;
		z[fac[0]][0]=1;
		for(int i=1;i<=30;i++)
			z[fac[0]][i]=z[fac[0]][i-1]*tmp%mo;
	}
	memset(f,0,sizeof f);
	num f; memset(f.e,0,sizeof f.e);
	f.v=C[0]=1;
	for(int i=1;i<=d;i++){
		C[i]=f.mult((n+1-(i-1)),i);
	}
}

int main(){
	freopen("sum.in","r",stdin);
	// freopen("sum.out","w",stdout);
	cin>>n>>m>>mo;
	if(mo==1){
		cout<<0<<endl;
		return 0;
	}
	if(n%2==0)n++;
	s=mo;while(s%2==0)s>>=1,t++;
	initC(s,m+10);
	ll c=0;
	ans=c=(n+1)/2;
	ll inv2=ksm(2,phi-1);
	for(int i=1;i<=m;i++){
		c=(C[i+1]-c)*inv2%s;
		if((i&1)==0)ans=(ans+c)%s;
	}
	int phis=phi;


	initC(1<<t,m+t+1);
	c=0;
	for(int i=m+2,z=0;z<t;i++,z++){
		c=(c+(1<<z)*((z&1)?-1:1)*C[i])%MO;
	}
	ll ans2=0;
	if(!(m&1))ans2=c;
	for(int i=m-1;~i;i--){
		c=(C[i+2]-2*c)%MO;
		if((i&1)==0)ans2=(ans2+c)%MO;
	}

	//CRT
	ll aaa=ans*MO%mo*ksm(MO,phis-1,mo)%mo+ans2*s%mo*ksm(s,phi-1,mo)%mo;
	cout<<(aaa%mo+mo)%mo<<endl;
}