快速排序算法----代码图解以及优化

快速排序(Quick Sort)的基本思想是：通过一趟排序将待排序记录分割成独立的两部分，其中一部分记录的关键字都比另一部分记录的关键字小，则可分别对这两部分记录继续进行排序，最后以达到整个序列有序的目的。

通过上方的基本思想不能明确的理解整个快速排序的思想，那么下面我们先通过图表的形式来分解一下快速排序的基本思想，在通过代码的形式进行明确的讲解。

例如数组 : int[] arr = {50, 10, 90, 30, 70, 40, 80, 60, 20}

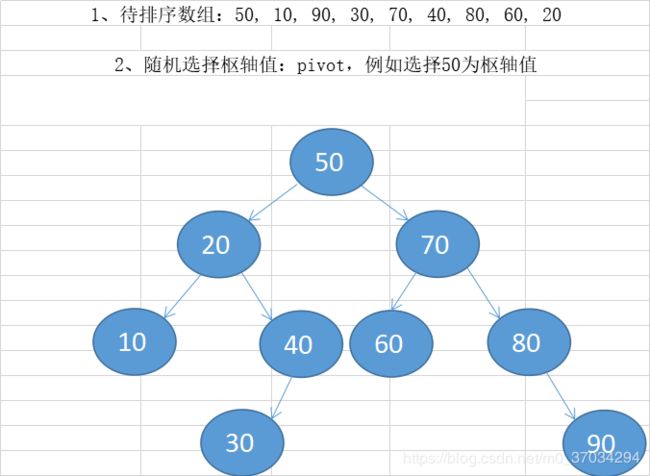
什么是枢轴：就是选择一个关键字例如50，然后想尽办法将他放到一个位置，使得他左边的值都比他小，右面的值都比它大。
我们先分析一下上面的整个过程，我们现在想用快速排序的方法排序上面的无序数组，这是我们选择了一个随机数作为枢轴，例如50，按照快速排序的思想我们需要将数组改变成一面都是比50小的数组，一面都是比50大的数组

1. 第一次选择枢轴50进行排序后枢轴的左面是20，10，40，30枢轴的右面是70，60，80，90
2. 第二次递归上面的排序方法排序拆开后的数组20,10,40,30，还是选择枢轴为20，那么他循环完成之后20的左面变成10，右面变成40，30。同理第一次枢轴的右面数组70，60，80，90，以70继续作为枢轴排序后变成70的左面为60右面为80,90。
3. 这就是整个快速排序的思想，当全部递归完成之后这个数组就变成了一个有序的数组，下面我们来看下实际操作代码怎么写吧

 	@Test
    public void test() {
        int[] arr = {50, 10, 90, 30, 70, 40, 80, 60, 20};
        //调用快速排序方法
        quickSort(arr);
        for (int i = 0; i < arr.length; i++) {
            System.out.println(arr[i]);
        }
    }
	//由于需要递归调用我们另封装了一个函数qSort(arr,0,arr.length-1),这里的0和arr.length-1是最小下标和最大下标
	void quickSort(int[] arr) {
        qSort(arr, 0, arr.length - 1);
    }

	private void qSort(int[] arr, int low, int high) {
		//定义变量枢轴
        int pivot;
        if (low < high) {
        	//获取枢轴下标位置，将arr[low....high]一分为2
            pivot = Partition(arr, low, high);
            //看里面的参数pivot-1，对低子表进行递归排序，例如上面说到的：20,10,40,30
            qSort(arr, low, pivot - 1);
            //看枢轴pivot+1，high，对高子表进行递归排序，例如上面说到的：70，60，80，90
            qSort(arr, pivot + 1, high);
        }
    }
    
    //核心方法
	private int Partition(int[] arr, int low, int high) {
		//变量枢轴
        int pivotkey；
        //用子表的第一个记录做枢轴
        pivotkey = arr[low];
        //从表的两端交替向中间扫描
        while (low < high) {
            while (low < high && arr[high] >= pivotkey) {
                high--;
            }
            swap(arr, low, high);
            while (low < high && arr[low] <= pivotkey) {
                low++;
            }
            swap(arr, low, high);
        }
        return low;
    }
    
	//交换下标位置数值
 	private void swap(int[] arr, int low, int high) {
        int temp = arr[low];
        arr[low] = arr[high];
        arr[high] = temp;
    }

执行结果

2019-04-10 16:59:22.559  INFO 29212 --- [           main] o.s.s.concurrent.ThreadPoolTaskExecutor  : Initializing ExecutorService 'applicationTaskExecutor'
2019-04-10 16:59:22.742  INFO 29212 --- [           main] com.example.demo.QuickApplicationTests   : Started QuickApplicationTests in 1.669 seconds (JVM running for 2.655)
10
20
30
40
50
60
70
80
90
2019-04-10 16:59:22.946  INFO 29212 --- [       Thread-2] o.s.s.concurrent.ThreadPoolTaskExecutor  : Shutting down ExecutorService 'applicationTaskExecutor'

有的同学可能会说上面的代码都是什么意思啊，看的不是很明白啊，这里我要提醒大家代码不能只看啊，要想完全想明白快速排序的运行原理，我还是建议大家打开电脑运行起来，通过断点debug走走流程这样你才能快速的理解排序的整个思想逻辑。

优化待续