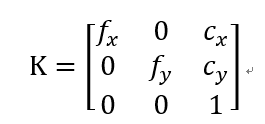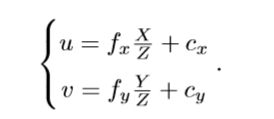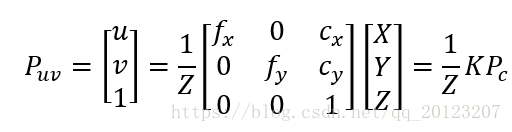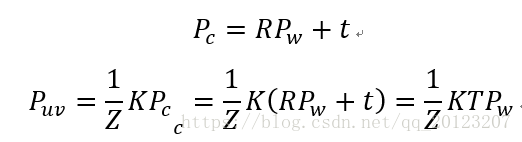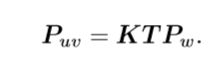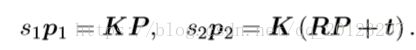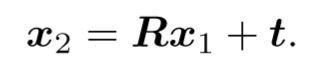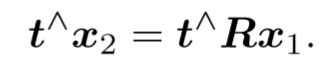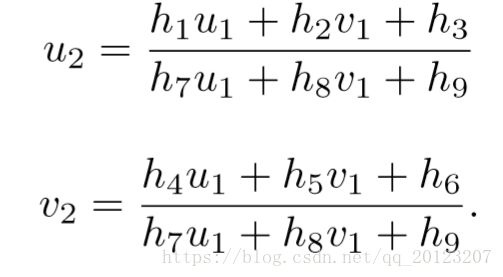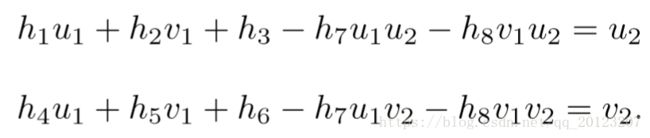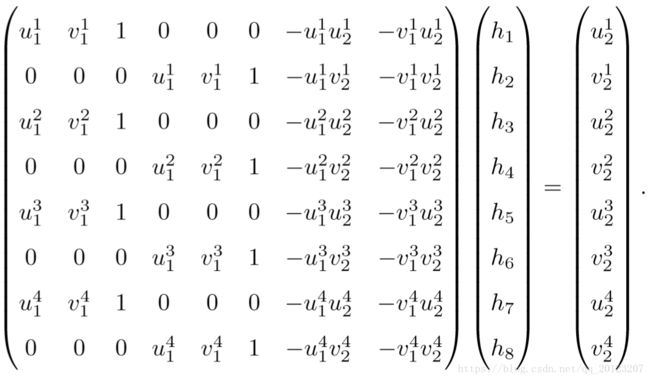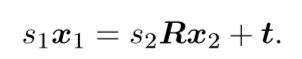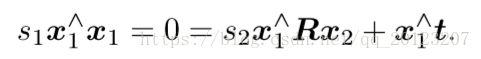ORB-SLAM2从理论到代码实现（四）：相机成像原理、基本矩阵、本质矩阵、单应矩阵、三角测量详解

本人邮箱[email protected],欢迎交流。转载请注明地址https://blog.csdn.net/qq_20123207/article/details/82492632

本篇我们继续上一篇博客的内容，一起学习ORBmatcher.cc。由于ORBmatcher.cc中有三角化和重投影等内容，所有我先写相机成像等多视图几何内容。

1.相机的成像原理

假设空间中有一点P，它在世界坐标系中的坐标为,在相机坐标系中的坐标为=[X,Y,Z]，在图片中的像素坐标为.

 

设相机内参为

 

则,，，的关系为：

上式中相机的位姿 R,t 又称为相机的外参数， 上式两侧都是齐次坐标。因为齐次坐标乘上非零常数后表达同样的含义，所以可以简单地把 Z 去掉： 

这就完成了从空间点到像素的过程。

2. 对极几何（参考高翔SLAM14讲）

假设图像,之间的运动为R，t。我们知道像素，，怎么求R，t呢？

在处的坐标为，则在处的坐标为，则

使用齐次坐标，写为

取

则 

两边同时左乘

两侧同时左乘 ,

由外积的意义，知左边为零，得一个简洁的式子

x我们把已知的 ，，带入上式，即可得到对极约束，

记基础矩阵（Fundamental Matrix）为F ，本质矩阵为（Essential Matrix）E。

 

本质矩阵E反映空间一点在不同视角摄像机下摄像机坐标系中的表示之间的关系。
基础矩阵F反映空间一点在不同视角摄像机下图像坐标系中的表示之间的关系。

F矩阵有如下性质：
1、秩为2；

2、F矩阵有七个自由度(3*3矩阵本身9个自由度，因为相差一个常数因子和行列式值为0两个条件，减掉2个自由度)，相差一个常数因此的意思是：kF(k!=0)也是基本矩阵，也就是说如果F是基本矩阵，那么kF也是基本矩阵，所以基本矩阵不唯一，在相差一个倍数的前提下是唯一的，也就是我们可以固定矩阵中某一个非零元素的值，这样自然少一个自由度。

E矩阵有如下性质：

1.秩为2；

2.本质矩阵 E 的奇异值必定是 [σ,σ,0]T 的形式。这称为本质矩阵的内在性质。

3.由于平移和旋转各有三个自由度，共有六个自由度，但由于尺度等价性，故 E 实际上有五个自由度。

3.单应矩阵

单应性是几何中的一个概念。单应性是一个从实射影平面到射影平面的可逆变换，直线在该变换下仍映射为直线。它是一对透视投影的组合射影变换群。它描述了当观察者视角改变时，被观察物体的感知位置会发生何种变化。射影变换并不保持大小和角度，但会保持重合关系和交比。

单应矩阵通常描述处于共同平面上的一些点，在两张图像之间的变换关系。

 

由于单应矩阵有8个自由度，所以用四对匹配点即可求出H。

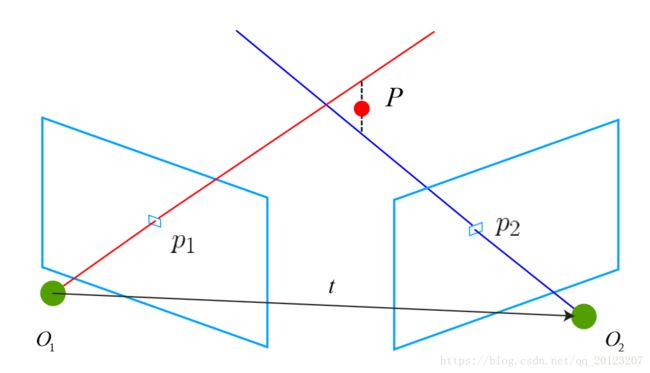
4. 三角测量

假设 x1,x2分别为两个特征点的归一化坐标，s1,s2,为两个特征点的深度值，R，t表示两帧之间的变换，有

现在方程左右两边左乘x1^,求x1的外积，那么就有

 

该式左侧为零，右侧可看成 s2 的一个方程，可以根据它直接求得 s2。有了 s2，s1 也 非常容易求出。

但是一般情况下R，t不一定精确，所以一般应用最小二乘求最优解。