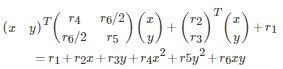OpenCV3学习(12.1) 稠密光流calcOpticalFlowFarneback
简介
光流(optic flow)是什么呢?名字很专业,感觉很陌生,但本质上,我们是最熟悉不过的了。因为这种视觉现象我们每天都在经历。从本质上说,光流就是你在这个运动着的世界里感觉到的明显的视觉运动(呵呵,相对论,没有绝对的静止,也没有绝对的运动)。例如,当你坐在火车上,然后往窗外看。你可以看到树、地面、建筑等等,他们都在往后退。这个运动就是光流。而且,我们都会发现,他们的运动速度居然不一样?这就给我们提供了一个挺有意思的信息:通过不同目标的运动速度判断它们与我们的距离。一些比较远的目标,例如云、山,它们移动很慢,感觉就像静止一样。但一些离得比较近的物体,例如建筑和树,就比较快的往后退,然后离我们的距离越近,它们往后退的速度越快。一些非常近的物体,例如路面的标记啊,草地啊等等,快到好像在我们耳旁发出嗖嗖的声音。
光流除了提供远近外,还可以提供角度信息。与咱们的眼睛正对着的方向成90度方向运动的物体速度要比其他角度的快,当小到0度的时候,也就是物体朝着我们的方向直接撞过来,我们就是感受不到它的运动(光流)了,看起来好像是静止的。当它离我们越近,就越来越大(当然了,我们平时看到感觉还是有速度的,因为物体较大,它的边缘还是和我们人眼具有大于0的角度的)。
光流的概念是Gibson在1950年首先提出来的。它是空间运动物体在观察成像平面上的像素运动的瞬时速度,是利用图像序列中像素在时间域上的变化以及相邻帧之间的相关性来找到上一帧跟当前帧之间存在的对应关系,从而计算出相邻帧之间物体的运动信息的一种方法。一般而言,光流是由于场景中前景目标本身的移动、相机的运动,或者两者的共同运动所产生的。
当人的眼睛观察运动物体时,物体的景象在人眼的视网膜上形成一系列连续变化的图像,这一系列连续变化的信息不断“流过”视网膜(即图像平面),好像一种光的“流”,故称之为光流(optical flow)。光流表达了图像的变化,由于它包含了目标运动的信息,因此可被观察者用来确定目标的运动情况。
研究光流场的目的就是为了从图片序列中近似得到不能直接得到的运动场。运动场,其实就是物体在三维真实世界中的运动;光流场,是运动场在二维图像平面上(人的眼睛或者摄像头)的投影。
那通俗的讲就是通过一个图片序列,把每张图像中每个像素的运动速度和运动方向找出来就是光流场。那怎么找呢?咱们直观理解肯定是:第t帧的时候A点的位置是(x1, y1),那么我们在第t+1帧的时候再找到A点,假如它的位置是(x2,y2),那么我们就可以确定A点的运动了:(ux, vy) = (x2, y2) - (x1,y1)。
那怎么知道第t+1帧的时候A点的位置呢? 这就存在很多的光流计算方法了。
1981年,Horn和Schunck创造性地将二维速度场与灰度相联系,引入光流约束方程,得到光流计算的基本算法。人们基于不同的理论基础提出各种光流计算方法,算法性能各有不同。Barron等人对多种光流计算技术进行了总结,按照理论基础与数学方法的区别把它们分成四种:基于梯度的方法、基于匹配的方法、基于能量的方法、基于相位的方法。近年来神经动力学方法也颇受学者重视。
在计算机视觉的空间中,计算机所接收到的信号往往是二维图片信息。由于缺少了一个维度的信息,所以其不再适用以运动场描述。光流场(optical flow)就是用于描述三维空间中的运动物体表现到二维图像中,所反映出的像素点的运动向量场。
当描述部分像素时,称为:稀疏光流
当描述全部像素时,称为:稠密光流
OpenCV中实现了不少的光流算法
1)calcOpticalFlowPyrLK
通过金字塔Lucas-Kanade 光流方法计算某些点集的光流(稀疏光流)。理解的话,可以参考这篇论文:”Pyramidal Implementation of the Lucas Kanade Feature TrackerDescription of the algorithm”,博客:https://blog.csdn.net/qq_30815237/article/details/87208319
2)calcOpticalFlowFarneback
用Gunnar Farneback 的算法计算稠密光流(即图像上所有像素点的光流都计算出来)。它的相关论文是:"Two-Frame Motion Estimation Based on PolynomialExpansion"
3)CalcOpticalFlowBM
通过块匹配的方法来计算光流。方法不支持图像金字塔匹配,不能用于跟踪大幅度的运动,具有C接口,但已被官方弃用。
4)CalcOpticalFlowHS
用Horn-Schunck 的算法计算稠密光流。方法不支持图像金字塔匹配,不能用于跟踪大幅度的运动具有C接口,但已被官方弃用。
5)calcOpticalFlowSF
简单光流法
稠密光流需要使用某种插值方法在比较容易跟踪的像素之间进行插值以解决那些运动不明确的像素,所以它的计算开销是相当大的。而对于稀疏光流来说,在他计算时需要在被跟踪之前指定一组点(容易跟踪的点,例如角点),因此在使用LK方法之前我们需要配合使用cvGoodFeatureToTrack()来寻找角点,然后利用金字塔LK光流算法,对运动进行跟踪。但个人感觉,对于少纹理的目标,例如人手,LK稀疏光流就比较容易跟丢。
Farneback 光流算法
光流法是利用图像序列中的像素在时间域上的变化、相邻帧之间的相关性来找到的上一帧跟当前帧间存在的对应关系,计算出相邻帧之间物体的运动信息的一种方法。光流法理解的关键点有:
- 核心问题:同一个空间中的点,在下一帧即将出现的位置
- 重要假设:光流的变化(向量场)几乎是光滑
- 角点处的光流能够通过角点的邻域完全确定下来,因此角点处的运动信息最为可靠;其次是边界的信息
光流法有着各种各样的分支,opencv 中的calcOpticalFlowPyrLK光流算法,实际上是一种稀疏特征点的光流算法,也就是说我们先找到那些(特征)点需要进行处理,然后再处理,下面介绍一种被广泛使用的经典稠密光流算法:Farneback 光流算法,它是一个全局性的密集光流算法,也就是对每一个点都进行光流计算,函数为calcOpticalFlowFarneback!
理论基础
1、将图像视为二维信号的函数(输出图像是灰度图像),因变量是二维坐标位置 ![]() ,并且利用二次多项式对于图像进行近似建模的话,会得到:
,并且利用二次多项式对于图像进行近似建模的话,会得到:
![]()
其中,A 是一个2×2的矩阵,b是一个2×1的矩阵,因此系数化之后,以上公式等号右侧可以写为:
2、如果将原有(笛卡尔坐标系)图像的二维信号空间,转换到以 (![]() )作为基函数的空间,则表示图像需要一个六维向量作为系数,代入不同像素点的位置 x,y求出不同像素点的灰度值。
)作为基函数的空间,则表示图像需要一个六维向量作为系数,代入不同像素点的位置 x,y求出不同像素点的灰度值。
void calcOpticalFlowFarneback(InputArray prevImg, InputArray nextImg,
InputOutputArray flow, double pyrScale, int levels,
int winsize, int iterations, int polyN,
double polySigma, int flags) 参数:
prevImg:输入第一个图
nextImg:输入第二个图
Flow:输出的光流矩阵。矩阵大小同输入的图像一样大,但是矩阵中的每一个元素可不是一个值,而是两个值,分别表示这个点在x方向与y方向的运动量(偏移量)。所以要把这个光流场矩阵显示出来还真的需要费点力。那么上面说的两幅图像与这个光流场是什么关系呢?如下:
![]()
pyrScale:一个构造图像金字塔的参数,一般就认为是0.5最好了,也就是将图像缩小一半。那么为什么要构造金字塔呢?这应该是与算法本身的设计有关,其实很多地方在检测特征的时候都会涉及到图像的金字塔,设想下如果有个特征点在原始尺寸与其缩小的尺寸下都是特征点的话,那么这个特征点就很有效了吧。
Levels:金字塔层数 ,常设值1,表示只使用原图像。Number of pyramid layers including the initial image. levels=1 means that no extra layers are created and only the original images are used
Winsize:相当于一个均值滤波的作用,窗口大小决定了其噪声的抑制能力什么的。越大越能 denoise 并且能够检测快速移动目标,但会引起模糊运动区域
Iterations:在每层金字塔上的迭代次数。
polyN:点与附近领域点之间的联系作用,一般为5,7等等即可。
polySigma :高斯标准差,一般为 1~1.5(函数处理中需要高斯分布权重)像素点的一个平滑水平。
Flags:一个标记,决定计算方法。包括 OPTFLOW_USE_INITIAL_FLOW 和 OPTFLOW_FARNEBACK_GAUSSIAN
详细参数说明参见:http://www.opencv.org.cn/opencvdoc/2.3.2/html/modules/video/doc/motion_analysis_and_object_tracking.html
源码解读可参考:https://blog.csdn.net/ironyoung/article/details/60884929
实例:
#include
using namespace cv;
Mat frame,preframe, gray, pregray;
Mat flowdata;
int main(int arc, char** argv) {
VideoCapture capture;
capture.open("vtest.avi");
namedWindow("input", CV_WINDOW_AUTOSIZE);
namedWindow("output", CV_WINDOW_AUTOSIZE);
capture.read(frame);
cvtColor(frame, pregray, CV_BGR2GRAY);
while (capture.read(frame)) {
imshow("input", frame);
cvtColor(frame, gray, CV_BGR2GRAY);
calcOpticalFlowFarneback(pregray, gray, flowdata, 0.5, 3, 15, 3, 5, 1.5, 0);
cvtColor(pregray, preframe, CV_GRAY2BGR);
for (int row = 0; row < preframe.rows; row++) {
for (int col = 0; col < preframe.cols; col++) {
const Point2f fxy = flowdata.at(row, col);
if (fxy.x > 2 || fxy.y > 2) {
circle(preframe, Point(col, row), 2, Scalar(0, 255, 0), 2);
}
}
}
imshow("output", preframe);
char c = waitKey(100);
if (c == 27) {
break;
}
}
capture.release();
waitKey(0);
return 0;
}
from:https://blog.csdn.net/zouxy09/article/details/8683859
from:https://blog.csdn.net/qq_24946843/article/details/82733373