2020百度之星 初赛二 1002 Distance 找规律 有问题的代码

Distance Accepts: 826
Submissions: 2880
Time Limit: 2000/1000 MS (Java/Others)
Memory Limit: 65536/65536 K (Java/Others)
Problem Description

小沃沃所在的世界是一个二维平面。他有 nnn 个朋友，第 iii 个朋友距离他的距离为 a[i]a[i]a[i]，小沃沃并不知道这些朋友具体在什么点上。

请问在最优情况下，小沃沃的朋友两两之间的欧几里得距离的和的最小值是几？

假设小沃沃的位置为 P0=(x0,y0)P_0 = (x_0,y_0)P0​=(x0​,y0​)，第 iii 个朋友的位置为 Pi=(xi,yi)P_i = (x_i,y_i)Pi​=(xi​,yi​)，对于所有的 iii，需要满足 dist(P0,Pi)=a[i]dist(P_0, P_i) = a[i]dist(P0​,Pi​)=a[i]，并且∑i=1n−1∑j=i+1ndist(Pi,Pj)\sum_{i=1}^{{n-1}{\sum_{j=i+1}}{n}{dist(P_i,P_j)}}∑i=1n−1​∑j=i+1n​dist(Pi​,Pj​) 最小，其中 dist(X,Y)dist(X,Y)dist(X,Y) 为连接点 XXX 和点 YYY 的线段的长度。xi,yix_i,y_ixi​,yi​ 都可以是任意实数。
Input

第一行一个正整数 test(1≤test≤10)test(1 \leq test \leq 10)test(1≤test≤10) 表示数据组数。

对于每组数据，第一行一个正整数 n(1≤n≤100000)n(1 \leq n \leq 100000)n(1≤n≤100000)。

接下来一行 nnn 个整数，第 iii 个整数 aia[i](1 \leq a[i] \leq 1000000000)ai 表示第 iii 个朋友和小沃沃的距离。
Output

对每组数据输出一行一个数，表示 ∑i=1n−1∑j=i+1ndist(Pi,Pj)\sum_{i=1}^{{n-1}{\sum_{j=i+1}}{n}{dist(P_i,P_j)}}∑i=1n−1​∑j=i+1n​dist(Pi​,Pj​) 的最小值。答案需要四舍五入到整数。
Sample Input

2
2
3 5
5
1 2 3 4 5

Sample Output

2
20

---

很容易想到所有点在同一条直线上才能得到最优的答案
如图

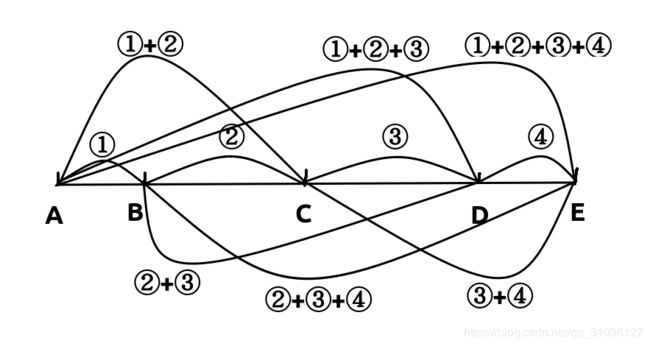
可以观察到规律

      ①    ②     ③     ④     ⑤    ⑥
--------------------------
2:个点 1
3个点: 2    2
4个点: 3    4      3
5个点: 4    6      6      4
6个点: 5    8      9      8      5
7个点: 6   10     12     12     10    6

这题有一个奇怪的地方,希望有大佬看见能指点一二

如下 : 如果不加括号可以ac,加了就wa

• sum += (a[i+1] - a[i]) * (i * ( n - i ) );这个会wa
• sum += (a[i+1] - a[i]) * i * (n - i);这个就能ac

#define debug
#ifdef debug
#include 
#include "/home/majiao/mb.h"
#endif

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define MAXN (int(1e6+7))
#define ll long long
#define INF (0x7f7f7f7f)
#define fori(lef, rig) for(int i=lef; i<=rig; i++)
#define forj(lef, rig) for(int j=lef; j<=rig; j++)
#define fork(lef, rig) for(int k=lef; k<=rig; k++)
#define QAQ (0)

using namespace std;

#ifdef debug
#define show(x...)                                 \
	do {                                           \
		cout << "\033[31;1m " << #x << " -> ";     \
		err(x);                                    \
	} while (0) 
#else
#define show(x...)  
#endif

void err() { cout << "\033[39;0m" << endl; }
template<typename T, typename... A>
void err(T a, A... x) { cout << a << ' '; err(x...); }

namespace FastIO {

	char print_f[105];
	void read() { }
	void print() { putchar('\n'); }

	template <typename T, typename... T2>
		inline void read(T &x, T2 &... oth) {
			x = 0;
			char ch = getchar();
			ll f = 1;
			while (!isdigit(ch)) {
				if (ch == '-') f *= -1; 
				ch = getchar();
			}
			while (isdigit(ch)) {
				x = x * 10 + ch - 48;
				ch = getchar();
			}
			x *= f;
			read(oth...);
		}
	template <typename T>
		inline void put(T x) {
			if(x==0) { putchar('0'); putchar('\n'); return; }
			if(x<0) { putchar('-'); x = -x; }
			int num=0;
			char ch[128];
			while(x) ch[++num] = x % 10 + '0', x /= 10;
			while(num) putchar(ch[num--]);
			putchar('\n');
		}
}; // namespace FastIO
using FastIO::read;
using FastIO::put;

int n, m, Q, K, tmin = INF;

ll a[MAXN], b[MAXN], c[MAXN];

signed main() {
#ifdef debug
	freopen("test", "r", stdin);
//	freopen("out_main", "w", stdout);
	clock_t stime = clock();
#endif
	read(Q);
	while(Q--) {
		read(n);
		for(int i=1; i<=n; i++) read(a[i]);
		sort(a+1, a+1+n);
		ll sum = 0;
#if 1
		for(int i=1; i<n; i++) //不能 AC
			sum += (a[i+1] - a[i]) * (i * ( n - i ) );
#else
		for(int i=1; i<n; i++)
			sum += (a[i+1] - a[i]) * i * (n - i);
#endif
		printf("%lld\n", sum);
	}




#if 0
		for(int i=n-1, timer=1; i>=1; i--, timer++) {
			c[i] = timer * i;
		}
#endif









#ifdef debug
	clock_t etime = clock();
#endif 
	return 0;
}