【模拟】ZJOI2014&BZOJ3519消棋子
传送门
注:
图的方向要注意!如果你把方向看反了,样例仍然可以过(然而几乎所有测试数据都过不了)。
样例图例如下:
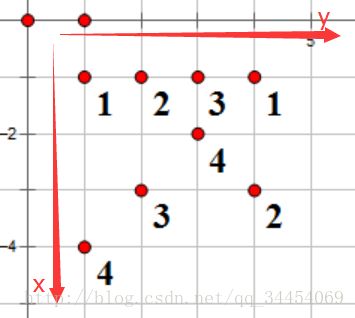
题目中给出,每种颜色只有2个,而且最多有100000种颜色。
那么很容易想到暴力算法。
用set分每行每列储存所有的点:
如一点坐标为(x,y)
那么就在y列插入x,同时在x行插入y
这样就可以通过迭代器,快速找到某个点每行每列相邻的的点。
对于1问,主要通过set的lower_bound来实现找最接近的点。
再写一个check检查是否为有效操作,如果是就删除这两个点。
对于2问,可以先把所有点扫一遍,找到可以删除的点,将其删除。
删除之后,就可能新增其他的可删除的点,简单分析可知,能够新增的点,与它相对应的点的连线一定经过删除的这个点(可以结合图像看一下)。
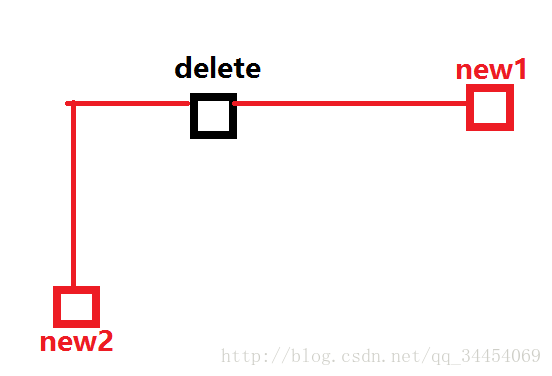
那么,在删除每个点时,向周围四个方向分别找到最近的点,再看这四个点能否可以删除。显然这是一个递归操作。
不过。。真正的难点是如何码代码。。
有一个实现细节:当你删除点之后,向周围四个方向找点,这时用check必须返回可以删除的点的颜色信息,否则会出现如下情况:
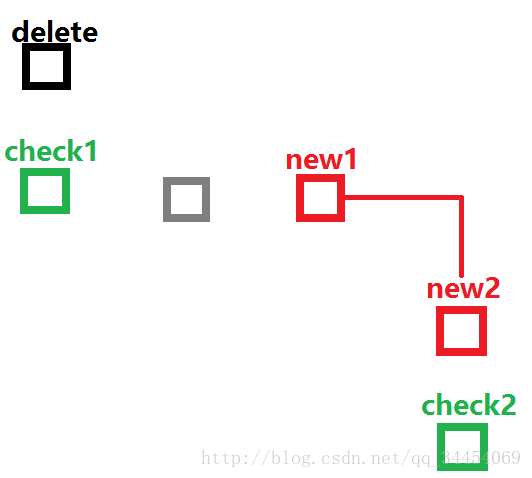
如果你只返回可不可行,那么就会把check1,check2删除,然而其实能删除的是new1和new2。
#includeint ,int> >del,l1,r1;
vector<int> dec;
set<int> l[MAXN],r[MAXN];
mapint ,int>,int> col;
int check(int x,int y,char c1,char c2){
cnta=0;
if(col[make_pair(x,y)]!=0)
return 0;
if(c1=='U'||c2=='U'){
xa[cnta]=x;
set<int>::iterator it=r[x].lower_bound(y);
if(it==r[x].begin())
return 0;
it--;
ya[cnta]=*it;
cnta++;
}
if(c1=='D'||c2=='D'){
xa[cnta]=x;
set<int>::iterator it=(r[x].lower_bound(y));
if(it==r[x].end())
return 0;
ya[cnta]=*it;
cnta++;
}
if(c1=='L'||c2=='L'){
ya[cnta]=y;
set<int>::iterator it=l[y].lower_bound(x);
if(it==l[y].begin())
return 0;
it--;
xa[cnta]=*it;
cnta++;
}
if(c1=='R'||c2=='R'){
ya[cnta]=y;
set<int>::iterator it=(l[y].lower_bound(x));
if(it==l[y].end())
return 0;
xa[cnta]=*it;
cnta++;
}
//PF("[%d %d %d %d]",x1,ya[0],xa[1],ya[1]);
return col[make_pair(xa[0],ya[0])]*(col[make_pair(xa[0],ya[0])]==col[make_pair(xa[1],ya[1])]);
}
char s1[5],s2[5],slr[3]={'L','R'},sud[3]={'U','D'};
struct node{
int x,y;
char ch1,ch2;
}ans[MAXN];
inline void de(int x,int y){
l[y].erase(x);
r[x].erase(y);
col[make_pair(x,y)]=0;
}
void dele(int,int);
void work(int x1,int y1,int x2,int y2){
int cc=col[make_pair(x1,y1)];
if(x1==x2){
if(y1if(check(x1,y1+1,'U','D')==cc){
de(x1,y1);
de(x2,y2);
ans[++tot].x=x1;
ans[tot].y=y1+1;
ans[tot].ch1='L';
ans[tot].ch2='R';
dele(x1,y1);
dele(x2,y2);
}
}
else{
if(check(x1,y1-1,'U','D')==cc){
de(x1,y1);
de(x2,y2);
ans[++tot].x=x1;
ans[tot].y=y1-1;
ans[tot].ch1='L';
ans[tot].ch2='R';
dele(x1,y1);
dele(x2,y2);
}
}
return ;
}
if(y1==y2){
if(x1if(check(x1+1,y1,'L','R')==cc){
de(x1,y1);
de(x2,y2);
ans[++tot].x=x1+1;
ans[tot].y=y1;
ans[tot].ch1='D';
ans[tot].ch2='U';
dele(x1,y1);
dele(x2,y2);
}
}
else{
if(check(x1-1,y1,'L','R')==cc){
de(x1,y1);
de(x2,y2);
ans[++tot].x=x1-1;
ans[tot].y=y1;
ans[tot].ch1='D';
ans[tot].ch2='U';
dele(x1,y1);
dele(x2,y2);
}
}
return ;
}
int tlr;
int tud;
if(x10;
else
tlr=1;
if(y10;
else
tud=1;
//PF("(%d %d %c %c %d)\n",x2,y1,sud[1-tud],slr[tlr]);
if(check(x2,y1,sud[1-tud],slr[tlr])==cc){
de(x1,y1);
de(x2,y2);
ans[++tot].x=x2;
ans[tot].y=y1;
ans[tot].ch1=slr[1-tud];
ans[tot].ch2=sud[tlr];
dele(x1,y1);
dele(x2,y2);
}
else if(check(x1,y2,sud[tud],slr[1-tlr])==cc){
de(x1,y1);
de(x2,y2);
ans[++tot].x=x1;
ans[tot].y=y2;
ans[tot].ch1=slr[tud];
ans[tot].ch2=sud[1-tlr];
dele(x1,y1);
dele(x2,y2);
}
}
void dele(int x,int y){
int xu,yu,xd,yd,xl,yl,xr,yr;
xu=x;
set<int>::iterator it=r[x].lower_bound(y);
if(it!=r[x].begin()){
it--;
yu=*it;
int si=col[make_pair(xu,yu)];
work(xu,yu,a1[si]+a3[si]-xu,a2[si]+a4[si]-yu);
}
xd=x;
it=(r[x].lower_bound(y));
if(it!=r[x].end()){
yd=*it;
int si=col[make_pair(xd,yd)];
work(xd,yd,a1[si]+a3[si]-xd,a2[si]+a4[si]-yd);
}
yl=y;
it=l[y].lower_bound(x);
if(it!=l[y].begin()){
it--;
xl=*it;
int si=col[make_pair(xl,yl)];
work(xl,yl,a1[si]+a3[si]-xl,a2[si]+a4[si]-yl);
}
yr=y;
it=(l[y].lower_bound(x));
if(it!=l[y].end()){
xr=*(l[y].lower_bound(x));
int si=col[make_pair(xr,yr)];
work(xr,yr,a1[si]+a3[si]-xr,a2[si]+a4[si]-yr);
}
}
int main(){
freopen("eliminate.in","r",stdin);
freopen("eliminate.out","w",stdout);
int x,y;
SF("%d%d",&R,&C);
SF("%d",&n);
for(int i=1;i<=n;i++){
SF("%d%d%d%d",&xa[0],&ya[0],&xa[1],&ya[1]);
a1[i]=xa[0];
a2[i]=ya[0];
a3[i]=xa[1];
a4[i]=ya[1];
r[xa[0]].insert(ya[0]);
l[ya[0]].insert(xa[0]);
r[xa[1]].insert(ya[1]);
l[ya[1]].insert(xa[1]);
col[make_pair(xa[0],ya[0])]=i;
col[make_pair(xa[1],ya[1])]=i;
}
SF("%d",&m);
for(int i=1;i<=m;i++){
SF("%d%d",&x,&y);
SF("%s",s1);
SF("%s",s2);
if(s1[0]=='L'||s1[0]=='U')
s1[0]='L'+'U'-s1[0];
if(s2[0]=='L'||s2[0]=='U')
s2[0]='L'+'U'-s2[0];
if(s1[0]=='R'||s1[0]=='D')
s1[0]='R'+'D'-s1[0];
if(s2[0]=='R'||s2[0]=='D')
s2[0]='R'+'D'-s2[0];
//PF("(%d %d %c %c %d)",x,y,s1[0],s2[0],check(x,y,s1[0],s2[0]));
if(check(x,y,s1[0],s2[0])!=0){
//PF("{%d %d %d %d}",xa[0],ya[0],xa[1],ya[1]);
dec.push_back(col[make_pair(xa[0],ya[0])]);
del.push_back(make_pair(xa[0],ya[0]));
del.push_back(make_pair(xa[1],ya[1]));
de(xa[0],ya[0]);
de(xa[1],ya[1]);
cnt++;
}
//PF("\n");
}
PF("%d\n",cnt);
for(int i=0;i2];
}
for(int i=1;i<=n;i++){
if(col[make_pair(a1[i],a2[i])]!=0)
work(a1[i],a2[i],a3[i],a4[i]);
}
PF("%d\n",tot);
for(int i=1;i<=tot;i++)
PF("%d %d %c %c\n",ans[i].x,ans[i].y,ans[i].ch1,ans[i].ch2);
}