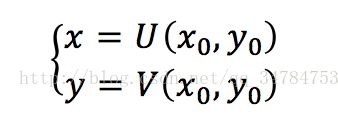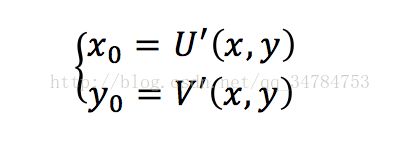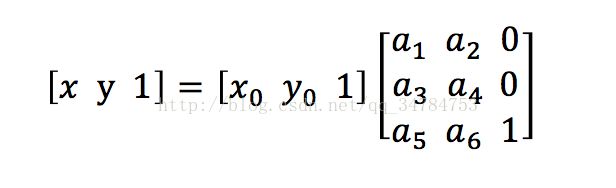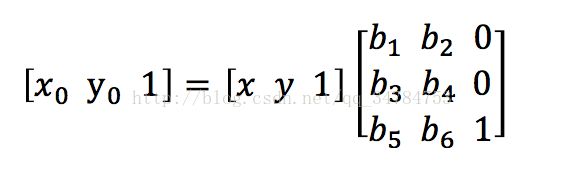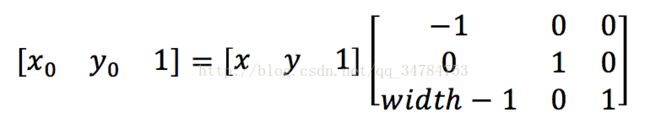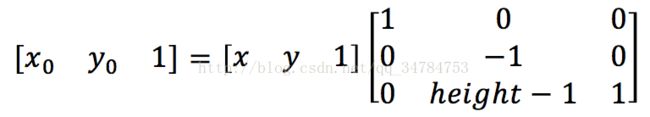【OpenCV图像处理】四、图像的几何变换(上)
图像的几何变换是指在不改变图像像素的前提下对图像像素进行空间几何变换。常见的变换有距离变换,坐标映射,平移,镜像,旋转,缩放和仿射变换等等。
也就是说,图像的几何变换就是建立一种源图像像素与变换后的图像像素之间的映射关系。也正是通过这种映射关系可以知道原图像任意像素点变换后的坐标,或者是变换后的图像在原图像的坐标位置等。用简单的数学公式可以表示为
其中,x,y代表输出图像像素的坐标,x0,y0表示输入图像的像素坐标,而U,V表示的是两种映射关系,需要说明的是,映射关系可以是线性关系,也可以是多项式关系
从上面的映射关系可以看到,只要给出了图像上任意的像素坐标,都能够通过对应的映射关系获得几何变换后的像素坐标。这种将输入映射到输出的过程我们称之为“向前映射”。但是在实际应用中,向前映射会出现如下几个问题:
a.浮点数坐标,如(1,1)映射为(0.5,0.5),显然这是一个无效的坐标,这时我们可以使用插值算法进行进一步处理。
b.映射不完全和映射重叠。
映射不完全是说输入图像的像素总数小于输出的像素总数,这会使得输出图像的部分像素与原始图像并没有映射关系,如进行放大操作。映射重叠是与映射不完全正好相反,输出图像会存在映射后的像素重叠。
为了克服前向映射的这些不足,因此引进了“后向映射”,它的数学表达式为:
同样的,x,y表示输出图像像素的坐标,x0,y0表示输入图像像素的坐标,U'和V'表示两种映射方式。
可以看出,后向映射与前向映射刚好相反,它是由输出图像的像素坐标反过来推算该像素为在源图像中的坐标位置。这样,输出图像的每个像素值都能够通过这个映射关系找到对应的为止。而不会造成上面所提到的映射不完全和映射重叠的现象。
在实际处理中基本上都运用向后映射来进行图像的几何变换。
在使用过程中,如果在一些不改变图像大小的几何变换中,向前映射还是十分有效的,向后映射主要运用在图像的旋转的缩放中,因为这些几何变换都会改变图像的大小。
在本篇文章里图像的几何变换全部都采用统一的矩阵表示法,形式如下:
这就是向前映射的矩阵表示法,其中x,y表示输出图像像素的坐标,x0,y0表示输入图像像素的坐标
同理,向后映射的矩阵表示为:
可以证明,向后映射的矩阵的表示正好是向前映射的逆变换。
4.1坐标映射。
4.1这部分文字内容一部分参考了朱伟等主编的《OpenCV图像处理编程实例》
图像的坐标映射是通过原图像与目标图像与目标图像之间建立一种映射关系,这种映射关系有两种,也就是上面所提到的向前映射和向后映射。
在OpenCV中提供了重映射相关的操作,而对于映射后出现了目标图像像素是非整数的情况,一般可以考虑插值或是向上取整。
void remap( InputArray src, OutputArray dst, InputArray map1, InputArray map2,int interpolation, borderMode=BORDER_CONSTANT,const Scalar& borderValue=Scalar());· INTER_NEAREST -最近邻插值
· INTER_LINEAR –双线性插值(默认值)
· INTER_CUBIC –双三次样条插值(逾4×4像素邻域内的双三次插值)
· INTER_LANCZOS4 -Lanczos插值(逾8×8像素邻域的Lanczos插值)
boderMode表示边界插值的类型,有默认值BORDER_CONSTANT,表示目标图像中“离群点(outliers)”的像素值不会被此函数修改。boderValue表示插值数值,其有默认值Scalar( ),即默认值为0。
使用OpenCV实现图像的坐标映射相关代码如下:
#include
#include
#include
#include
using namespace std;
using namespace cv;
int main()
{
Mat srcImage = imread("2345.jpg");
if (!srcImage.data)
{
cout << "读入图片错误!" << endl;
return -1;
}
imshow("原始图", srcImage);
//创建输出矩阵
Mat dstImage(srcImage.size(), srcImage.type());
//定义x和y方向的矩阵
Mat xMap(srcImage.size(), CV_32FC1);
Mat yMap(srcImage.size(), CV_32FC1);
//获取图像的宽和高
int rowNumber = srcImage.rows;
int colNumber = srcImage.cols;
//对图像进行遍历操作
for (int i = 0; i < rowNumber; i++)
{
for (int j = 0; j < colNumber; j++)
{
//x和y都进行翻转操作
xMap.at(i, j) = static_cast(srcImage.cols - j);
yMap.at(i, j) = static_cast(srcImage.rows - i);
}
}
//进行重映射操作
remap(srcImage, dstImage, xMap, yMap,
CV_INTER_LINEAR, BORDER_CONSTANT, Scalar(0, 0, 0));
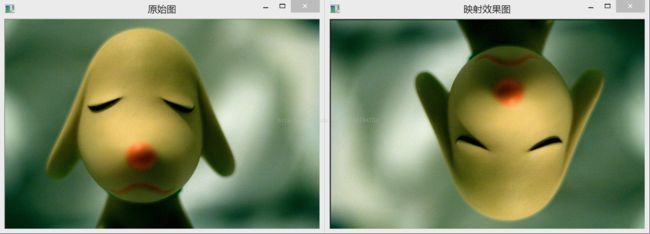
imshow("映射效果图", dstImage);
waitKey();
return 0;
} 运行后效果图为:
可以看出,图像上下和左右都进行了翻转操作。
4.2 平移变换
图像的平移变换是最简单的几何变换,就是将图像中所有像素的坐标分别加上或减去指定的水平和垂直偏移量,从而使整张图片出现移位的效果。
对于原始图像而言,它的正变换矩阵为:
而对于目标图像而言,其逆变换矩阵为:
平移变换用程序实现过程如下:
//实现图像的平移变换
#include
#include
#include
#include
using namespace std;
using namespace cv;
int main()
{
Mat srcImage, dstImage;
int xOffset, yOffset; //x和y方向的平移量
srcImage = imread("2345.jpg");
if (!srcImage.data)
{
cout << "读入图片错误!" << endl;
return -1;
}
dstImage.create(srcImage.size(), srcImage.type());
cout<< "请输入x方向和y方向的平移量:";
cin >> xOffset >> yOffset;
int rowNumber = srcImage.rows;
int colNumber = srcImage.cols;
//进行遍历图像
for (int i = 0; i < rowNumber; i++)
{
for (int j = 0; j < colNumber; j++)
{
//平移变换
int x = j - xOffset;
int y = i - yOffset;
//判断边界情况
if (x >= 0 && y >= 0 && x < colNumber && y < rowNumber)
dstImage.at(i, j) = srcImage.at(y,x);
}
}
imshow("原图像", srcImage);
imshow("平移后的图像", dstImage);
waitKey();
return 0;
}
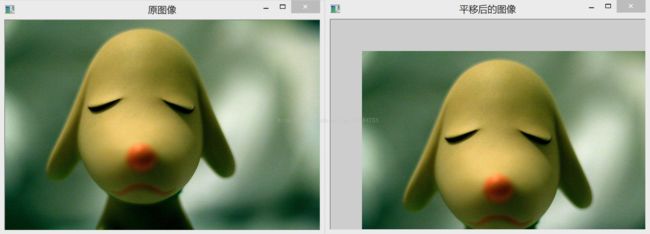
程序效果如下图所示:
这里x和y方向的平移量都取+50个像素
4.3 镜像变换
图像的镜像变换和数学上的轴对称非常类似,水平镜像和垂直镜像分别对应着以图像的水平中轴线和垂直中轴线为对称轴做对称变换操作。
总之,水平镜像变换产生的是原始图像的水平投影,类似于在镜子中显示的物体,而垂直镜像变换是原始图在垂直方向上进行投影,效果类似于水中的倒影。
基本原理:
a.水平镜像变换
设图像的宽度是width,则水平镜像变换的映射关系如下:
用矩阵可以表示为:
相应的逆运算矩阵如下:
可以发现,水平镜像变换的向前映射和向后映射的两个关系式相同,也就是说,将水平镜像变换得到的结果再做水平变化会得到原来的图像,从数学的角度上思考,这是显然的。同理,在垂直镜像变换中也有这样的结论。
b.垂直镜像变换
设变换的图像的高度为height,垂直镜像变换的映射关系如下:
使用矩阵可以表示为:
相应的逆运算为:
下面使用OpenCV和C++语言编程实现水平镜像变换和垂直镜像变换过程。
需要说明的是,在OpenCV中有flip函数可以实现镜像变换功能,函数说明如下:
void flip(InputArray src, OutputArray dst, int flipCode)//实现图像的镜像变换
//包括水平镜像和竖直镜像
#include
#include
#include
#include
using namespace std;
using namespace cv;
int main()
{
Mat srcImage, dstImage1,dstImage2;
srcImage = imread("2345.jpg");
dstImage1.create(srcImage.size(), srcImage.type());
dstImage2.create(srcImage.size(), srcImage.type());
//方法1,使用flip函数对图像进行水平镜像变换操作
flip(srcImage, dstImage1, 1); //第三个参数flipCode>0表示沿y轴做镜像
//方法2,遍历图像像素
int rowNumber = srcImage.rows;
int colNumber = srcImage.cols;
for (int i = 0; i < rowNumber; i++)
{
for (int j = 0; j < colNumber; j++)
{
dstImage2.at(i, j)[0] = srcImage.at(i, colNumber - j - 1)[0];
dstImage2.at(i, j)[1] = srcImage.at(i, colNumber - j - 1)[1];
dstImage2.at(i, j)[2] = srcImage.at(i, colNumber - j - 1)[2];
}
}
imshow("原图像", srcImage);
imshow("flip方法水平镜像", dstImage1);
imshow("遍历像素水平镜像", dstImage2);
//方法1,使用flip函数对元对象进行垂直镜像变换操作
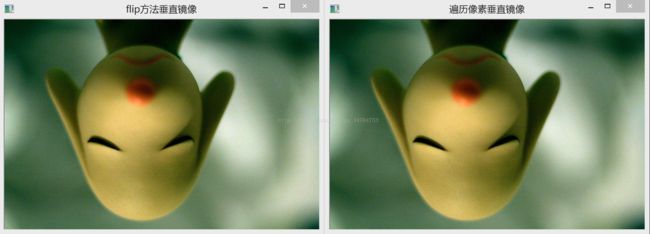
flip(srcImage, dstImage1, 0);
//方法2,遍历图像像素
for (int i = 0; i < rowNumber; i++)
{
for (int j = 0; j < colNumber; j++)
{
dstImage2.at(i, j)[0] = srcImage.at(rowNumber - i - 1, j)[0];
dstImage2.at(i, j)[1] = srcImage.at(rowNumber - i - 1, j)[1];
dstImage2.at(i, j)[2] = srcImage.at(rowNumber - i - 1, j)[2];
}
}
imshow("flip方法垂直镜像", dstImage1);
imshow("遍历像素垂直镜像", dstImage2);
waitKey();
return 0;
} 图像几何变换的上半部分就先写到这里。其余的几何变换将在下一篇中写出。