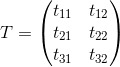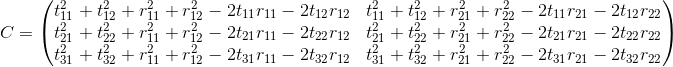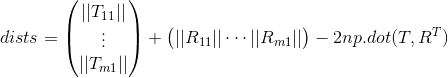深度学习与媒体计算②——kNN的优化与线性分类 (CS231n)

① Optimization of kNN algorithm kNN算法优化问题

kNN (k - nearest neighbors Algorithm) k近邻算法是一种易于实现的简单分类算法，下面我们结合 Assignment 1 中的 kNN 的这项作业以及python.numpy的一些特性，来讨论kNN的三种不同效率的算法实现。

(i) Double Loops 二重循环的朴素实现

对于算法的直接实现：第一重循环遍历测试数据集，第二重循环遍历训练数据集。使用测试数据项和每一个训练数据计算欧几里得距离L2，维护一个二维数组dist来记录距离信息。最后，在每一个测试数据对应的距离中选出前k个距离最小者，通过投票的方式选出该测试数据的所属类别。

python实现的代码如下

  def compute_distances_two_loops(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using a nested loop over both the training data and the 
    test data.

    Inputs:
    - X: A numpy array of shape (num_test, D) containing test data.

    Returns:
    - dists: A numpy array of shape (num_test, num_train) where dists[i, j]
      is the Euclidean distance between the ith test point and the jth training
      point.
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in xrange(num_test):
      for j in xrange(num_train):
        dists[i][j]=np.sqrt(np.sum(np.square(self.X_train[j,:] - X[i,:])))
    return dists

两重for循环所贡献的时间复杂度 T (n) = O(num_test*num_train), 效率极低。

(ii) Single Loop (Half Vectorization) 单重循环 (半向量化)

减少了一重遍历训练数据集的循环，将单项测试数据和整个训练集做L2运算，得到一个向量dists存储测试数据 i 到各个训练数据的距离。

Python 实现代码如下。

  def compute_distances_one_loop(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using a single loop over the test data.

    Input / Output: Same as compute_distances_two_loops
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train))
    for i in xrange(num_test):
      dists[i]=np.sqrt(np.sum(np.square(self.X_train - X[i,:])))
    return dists

时间复杂度 T (n) = O(num_test)，相较于前者有所优化。

(iii) No Loop 无循环，完全向量化的实现

这个实现策略需要一定的数学推导，下面我们降低维度，分别假设出如下的测试数据矩阵 T 和训练数据矩阵 R

根据欧几里得距离L2的计算公式，dist的矩阵化表示可以被简化成下句代码

那么差分平方和项矩阵C的原型为

根据完全平方公式展开后可以得到

显然：

（读者可以根据上式结合本式去验证）

所以经过推广后，完全向量化的dists计算值为

根据以上推导得到的Python代码如下。

  def compute_distances_no_loops(self, X):
    """
    Compute the distance between each test point in X and each training point
    in self.X_train using no explicit loops.

    Input / Output: Same as compute_distances_two_loops
    """
    num_test = X.shape[0]
    num_train = self.X_train.shape[0]
    dists = np.zeros((num_test, num_train)) 

    train = np.sum(np.square(self.X_train),axis=1)
    test = np.sum(np.square(X),axis=1)
    dists = np.sqrt(train+test.reshape(-1,1)-2*np.dot(X, self.X_train.T))
    return dists

这里需要解释的是test.reshape(-1,1)的意思是，将test数组转换成为列数为1的矩阵，-1代表行数不确定，根据展开后的结果确定行数。

test需要reshape的原因和python中广播的特性有关系，前者是一个 [5000,] 大小的张量，后者是[500,]大小的张量.后者需要确定列数之后才能够进行广播。（个人理解的大概意思是这样，可能有问题，欢迎在评论指正）

算法时间复杂度T (n) = O(1)，效率提升幅度很大。在Assignment1中会有一段时间对比的代码，效果非常清晰。但是问题在于，kNN的准确率一般只在27%左右，所以这并不是一个很适合进行图像分类的算法。

②线性分类 (Linear Classification)

kNN被我们所否定的原因主要有两个：1. 准确率低，不适用进行分类；2. 空间开销大，必须要把数据集存到本地进行运算，而图像数据集通常有几个G那么大，这么做的话对内存压力太大。

这里我们再回顾一下整个图像分类问题：我们向分类器输入一张待分类的图片 x ∈ ，分类器经过带标签的数据集训练后，可以分辨出K类数据。分类器根据图片内的特征，结合自身具备的性质来确认图片中对象的所属类别，最后输出对各个类别的打分，选取分值最高者作为这张图片的所属类别。假设该分类过程的对应法则为 f，则有 .在本模块，我们使用的则是最简单的线性对应法则。

这里我们令输入图像xi展开成大小为[D,1]的列向量，W的大小为[K,D]，b为[K,1]。W被称作Weight权重，b为偏置向量Bias Vector。

相较于kNN，线性分类具有如下的几个特点：

1. 线性分类器的主要参数是W，b。因此对于一个分类器而言它只需要具备两个参数值即可，训练集数据只有在学习 W，b 的值的时候需要，学习完成之后就可以删除掉存在本地的训练集，降低系统开销。

2. W权重矩阵的每一行都对应着一个类别的全部特征。

3. 线性分类器通过测试数据和W做乘法来并行地完成多个类别的匹配，运算速度加快。

那么 W 权重矩阵到底是什么？ 实际上，我们可以把 W 理解成一个模板矩阵，对于每个测试数据 (图像) 而言，各个类别的得分都是通过它和 W 做内积来完成的。两个向量的内积运算结果受特征匹配程度高的那个向量影响较大，因此可以通过得分的方式来比较出一张测试图像和哪个类别更匹配。下图摘自CS231n的页面，图中对模板做出了可视化的操作，更易于直观理解W的意义。

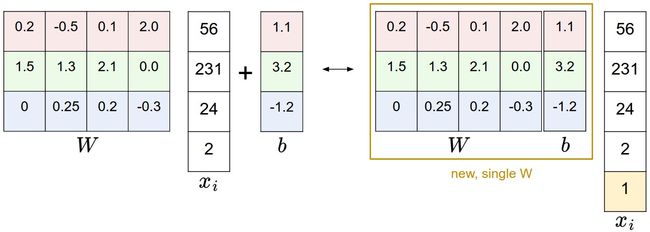
通常情况下，我们会把 W 和 b 用增广矩阵的形式表达，与此同时，特征向量xi会增加一个常数1来匹配线性分类器中的运算。

下图摘自 CS231n

下几篇博客将重点讲解深度学习和神经网络，相关机器学习的基本概念将在后期的博客中补充。

本期参考文献：

CS231n 课程主页