堆排序算法及其Java实现(以大根堆为例)
(二叉)堆数据结构是一种数组对象,如图所示(下标从0开始),它完全可以被视为一棵完全二叉树。
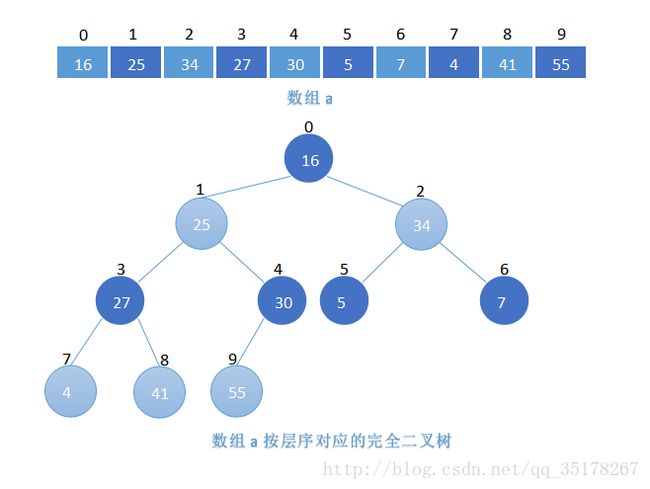
接下来要出现的几个词语,这里介绍一下:
length[A]: 数组A中元素的个数
heap-size[A]: 存放在数组A中堆的元素的个数,是要排序的元素的个数,在进行堆排序时,这个是会变的(减1)
A[0]是树的根,A[i]是数组中的第i个元素(从0开始计数)
PARENT(i): 第i个元素父结点的位置,值为 (i - 1)/2
LEFT(i): 第i个元素左孩子的位置,值为2i + 1
RIGHT(i): 第i个元素右孩子的位置,值为 2i + 2
static int parent(int i) {
return (i - 1)/2;
}
static int left(int i) { //左孩子
return 2*i + 1;
}
static int right(int i) { //右孩子
return 2*i + 2;
}操作:
MAX-HEAPIFY: 保持大根堆性质,运行时间O(lg n)
BUILD-MAX-HEAP: 大根堆初始建堆,即在无序的输入基础上建堆,运行时间O(n)
HEAPSORT: 堆排序,对一个数组进行原地排序,运行时间O(n*lg n)
一、MAX-HEAPIFY(保持大根堆性质)
大根堆的性质:A[PARENT(i)] >= A[i],MAX-HEAPIFY是对大根堆进行操作的重要子程序,后面要经常用到。
输入:以a[i]为根结点的子树,且以a的左孩子和a的右孩子为根节点的子树都满足大根堆性质
输出:树形没有变,但结点顺序可能发生改变的子树(该树的所有子树的根节点的值都大于它左右孩子的值,保持了大根堆性质)
static void maxHeapfy(int []a,int i,int heapSize) { //数组a,第i个结点,heapSize是数组中实际要排序的元素的长度
int left = left(i); //有的时候能够递归到叶子结点,叶子结点无后继,下面两个if都注意到了这一点
int right = right(i);
int largest = i;
if(left < heapSize && a[left] > a[largest]) { //
largest = left;
}
if(right < heapSize && a[right] > a[largest])
{
largest = right;
}
if(largest != i) { //把最大值给父结点
a[largest] = a[largest] ^ a[i];
a[i] = a[largest] ^ a[i];
a[largest] = a[largest] ^ a[i];
maxHeapfy(a,largest,heapSize); //发生交换之后还要保证大根堆性质
}
}二、BUILD-MAX-HEAP(初始建堆)
输入:无序的一组数
输出:一组数,按层序对应一棵完全二叉树,并且在它的每个子树中,根节点的值都大于其后代结点的值
步骤:自底向上,从最后一个非叶子结点开始调用MAX-HEAPFY操作,以下图为例
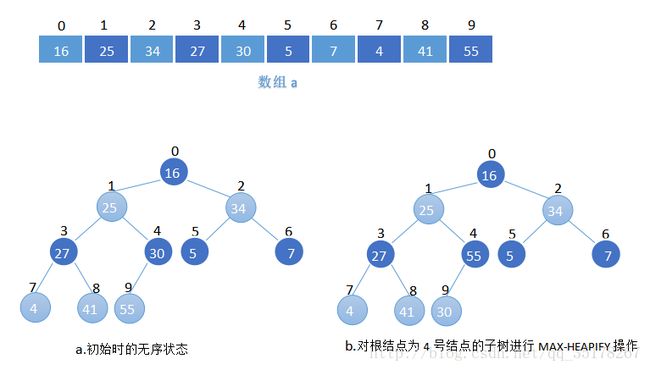
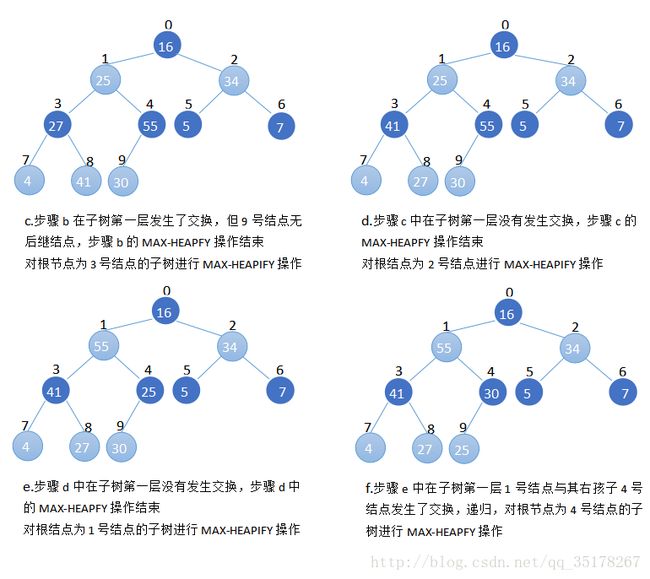
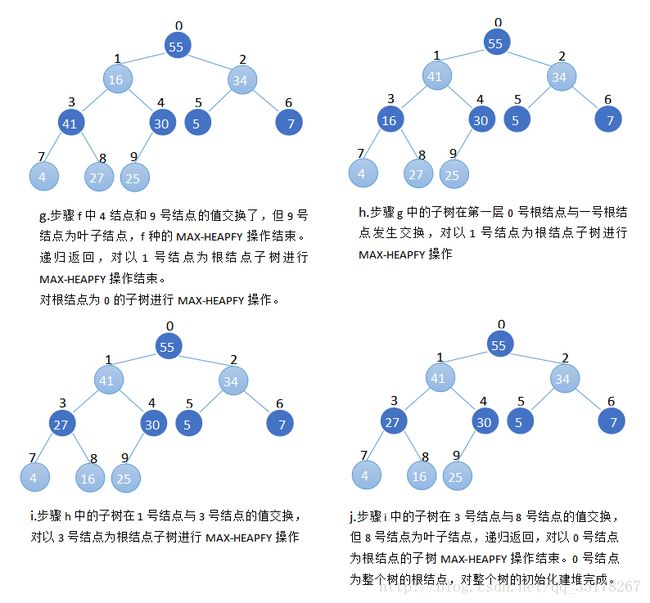
代码实现:
static void buildMaxHeap(int []a,int heapSize) {
for(int i = (heapSize-1)/2;i >= 0;i--) {
maxHeapfy(a,i,heapSize);
}
}三、堆排序(HEAPSORT)
通过初始建堆,数组中最大的元素在A[0],此时我们把A[0]与A[n-1]互换,对新数组A[0]~A[n-2]重新建堆,然后第二大的元素又落在了A[0]的位置上,此时我们把A[0]与A[n-2]互换…..以此类推,堆的大小由n-1一直降到2,我们得到原输入序列的升序排列
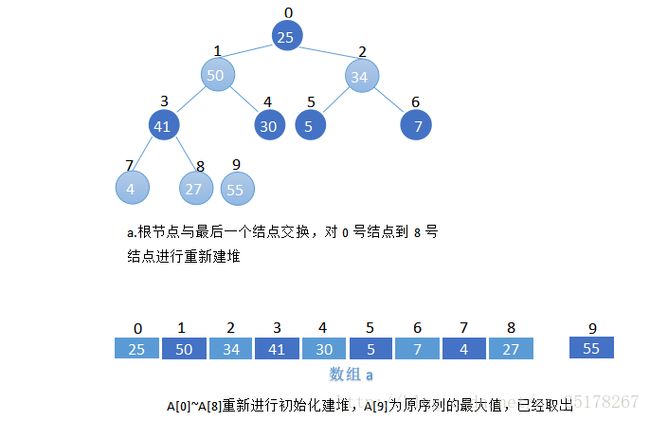
代码:
static void heapSort(int []a) {
for(int i = a.length-1;i > 0;i--) {
buildMaxHeap(a,i+1); //堆的大小从n到2
a[i] = a[0] ^ a[i]; //交换
a[0] = a[0] ^ a[i];
a[i] = a[0] ^ a[i];
}
}在初始建堆之后,原根结点的左右子树均满足最大堆的性质,所以实际上在对A[0]~A[n-2]进行初始建堆的时候,只有在根结点A[0]处执行了MAX-HEAPIFY操作,下面的代码换一种更直观的写法:
static void heapSort(int []a) {
int len = a.length;
buildMaxHeap(a,len); //初始建堆
a[len-1] = a[0] ^ a[len-1]; //交换
a[0] = a[0] ^ a[a.length-1];
a[len-1] = a[0] ^ a[len-1];
for(int i = 1;i
maxHeapfy(a,0,len-i);
a[len-1-i] = a[0] ^ a[len-1-i]; //交换
a[0] = a[0] ^ a[len-1-i];
a[len-1-i] = a[0] ^ a[len-1-i];
}
} //如有错误,欢迎指正
整个程序代码如下:
package ex;
import java.util.Arrays;
public class Sort {
public static void main(String args[]) {
int []a = new int[] {16,25,34,27,30,5,7,4,41,55};
Sort.heapSort(a);
System.out.println(Arrays.toString(a));
}
static int parent(int i) {
return (i - 1)/2;
}
static int left(int i) {
return 2*i + 1;
}
static int right(int i) {
return 2*i + 2;
}
static void maxHeapfy(int []a,int i,int heapSize) { //数组a,第i个结点,heapSize是数组种实际要排序的元素的长度
int left = left(i); //有的时候能够递归到叶子结点,叶子结点无后继,下面两个if都注意到了这一点
int right = right(i);
int largest = i;
if(left < heapSize && a[left] > a[largest]) { //
largest = left;
}
if(right < heapSize && a[right] > a[largest])
{
largest = right;
}
if(largest != i) { //把最大值给父结点
a[largest] = a[largest] ^ a[i];
a[i] = a[largest] ^ a[i];
a[largest] = a[largest] ^ a[i];
maxHeapfy(a,largest,heapSize); //发生交换之后还要保证大根堆性质
}
}
static void buildMaxHeap(int []a,int heapSize) {
for(int i = (heapSize-2)/2;i >= 0;i--) {
maxHeapfy(a,i,heapSize);
}
}
static void heapSort(int []a) {
int len = a.length;
buildMaxHeap(a,len); //初始建堆
a[len-1] = a[0] ^ a[len-1]; //交换
a[0] = a[0] ^ a[a.length-1];
a[len-1] = a[0] ^ a[len-1];
for(int i = 1;i1;i++) { //初始建堆之后还要排a.length-2次
maxHeapfy(a,0,len-i);
a[len-1-i] = a[0] ^ a[len-1-i]; //交换
a[0] = a[0] ^ a[len-1-i];
a[len-1-i] = a[0] ^ a[len-1-i];
}
}
}
//输出结果:
//[4, 5, 7, 16, 25, 27, 30, 34, 41, 55]