多目标优化_学习笔记（二）NSGA-II

前言

本篇博客出于学习交流目的，主要是用来记录自己学习多目标优化中遇到的问题和心路历程，方便之后回顾。过程中可能引用其他大牛的博客，文末会给出相应链接，侵删！

REMARK：本人纯小白一枚，0基础，如有理解错误还望大家能够指出，相互交流。也是第一次以博客的形式记录，文笔烂到自己都看不下去，哈哈哈

---

笔记（二）中记录在学习NSGA-II中的笔记

正文

NSGA-II作为多目标优化算法的经典算法之一，于2000年Srinivas 和 Deb 提出，相比较第一代非支配排序遗传算法NSGA而言具有以下改进：

1. 提出了快速非支配排序概念，将第一代算法的计算复杂度$O(M{N}^3)$降为$O(M{N}^2)$；
2. 添加精英机制，使得父代种群与子代种群共同竞争生成新种群，保证已经获得的最优解不丢失，有利于算法收敛性。（传统精英机制，构建一个外部种群用于保存从始至终的非支配解）；
3. 采用拥挤度度量算子，克服NSGA中认为指定共享参数的缺陷；

---

遗传算法回顾

NSGA-II属于遗传算法的变形，在正式理解算法之前，先对遗传算法进行简单的回顾，遗传算法含以下五步：
a.种群初始化
b.个体评价（计算适应度函数）
c.选择运算(Selection)，常用选择运算有轮盘赌选择法、随机遍历抽样法、锦标赛选择法；

简单介绍锦标赛机制（本算法用到的选择运算），在父代种群中随机选择$n$个个体，选择其中最优的个体放入子代种群，重复此步骤，每次都选择最优的个体直子代种群大小达到种群要求大小。

d.交叉运算(Crossover)，单点交叉，洗牌交叉等
e.变异运算(Mutation)

---

NSGA-II算法主要由三个部分组成,下文中将详细说明。
A、快速非支配方法
B、拥挤比较算子
C、主程序

具体算法

A、快速非支配方法

$>>>$ 传统排序方法：计算复杂度$O(M{N}^3)$，$M$为目标个数，$N$为种群大小。计算${\mathcal{F}}_1$（第一Pareto前沿）时，每个解需要和剩余$N-1$个解分别比较$M$次，所以计算复杂度为$O(M{N}^2)$，而对于最坏的情况，即每个解占一个前沿，每个前沿中只有一个解的时候，计算复杂度为$O(M{N}^3)$。

$>>>$快速非支配方法：计算复杂度$O(M{N}^2)$
先介绍两个变量：$n_p$表示为解$p$被几个解所支配，是一个数值；$S_p$表示解$p$支配哪些解，是一个解集合。借用博客中的图例可以很好的理解，这里真心表示感谢。

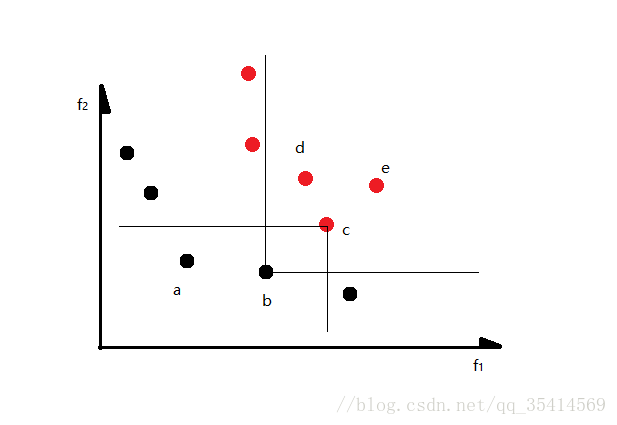
如上图所示，对$c$解而言，被$a，b$两个解支配，我们计算$n_c$为2；同理，解$b$支配三个解，我们得到$S_b=\left\{c,d,e\right\}$。

算法具体流程如下图所示

首先，遍历解集合中的所有解，并分别计算这些解对应的$n$值和$S$集合，对于$n=0$的解，表示该解为非支配解，划入${\mathcal{F}}_1$；接着，访问当前${\mathcal{F}}_{rank}$中每个Pareto最优解对应$S$集合中的解，当解被访问则$n$值减一，每完整遍历一次前沿面的序号rank增大1，其中若有解对应$n$值为0，则保存至下一前沿面${\mathcal{F}}_{rank+1}$中；重复上一步骤，直到所有解都划分到对应的前沿面中，得到$\mathcal{F}{1}\prec {F}{2} \prec \cdots $。

第一步中同传统排序算法，计算复杂度为$O(M{N}^2)$，第二步中，每个解最多被$N-1$个解支配，所以计算复杂度为$O(N^2)$，综合而言，快速非支配方法将传统方法的计算复杂度从$O(M{N}^3)$降低为$O(M{N}^2)$。

B、拥挤比较算子

为了弥补需人为设置共享函数的缺陷，作者提出了拥挤比较算子，保证了统一前沿的解多样性。

$>>>$密度估计：对同一个前沿面的解集合按各个目标分量大小排序，计算每个解在该分量下的两侧点的距离差值，而后进行累加各个分量上的距离作为拥挤系数，具体算法流程如下图所示

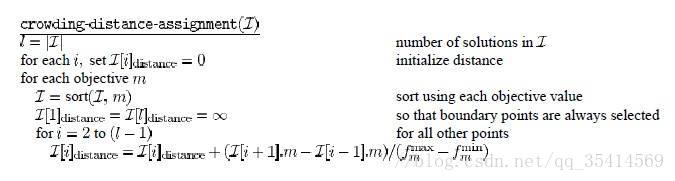
其中，$l$表示当前最优前沿面中解集合$\mathcal{I}$的大小。$\mathcal{I}{\left[i\right]}_{distance}$用于累加计算拥挤系数，对于每个解$i$的每个目标分量$m$ 计算该分量上排序后一个$i+1$与前一个点$i-1$相对差值作为分量上的拥挤度量，$f{}_m^{max}，f{}_m^{min}$分别表示目标分量$m$上的最大取值和最小取值。

在图中我们可以看出，对于解$i$计算得到的拥挤系数可以理解为是图中虚线所围成矩形的一半（对于两目标优化），位于头尾两端的解我们定义为无穷大。拥挤系数越大，越容易在遗传算法选择阶段被选择增强了同一前沿面的多样性。

C、主程序
掌握以上两部分算法后，从主程序了解整体算法思路，主要在选择策略部分区别于传统遗传算法。

$>>>$种群初始化
随机创建父代种群$P_0$，为父代种群利用快速非支配排序算法计算出非支配等级，并利用二进制锦标赛机制重组以及变异算子生成大小为$N$的子代种群。

$>>>$子代个体选择
下面是原文给出的新父代个体选择过程的计算复杂度和过程图例

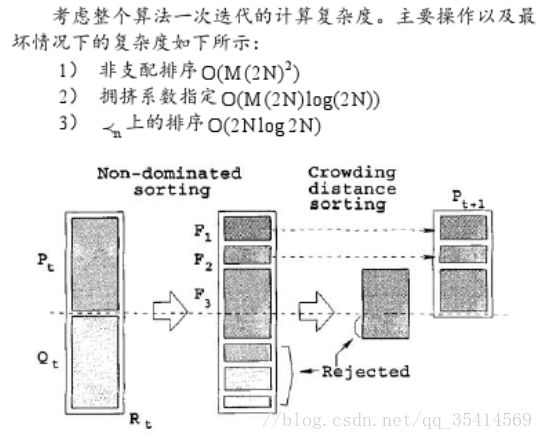
对于每个父代种群$P_t$，我们将其生成的子代种群$Q_t$与之合并为合并种群$R_t$，接着对新种群$R_t$利用快速非支配排序算法算法计算得到$R_t$中解得前沿排序，我们按照$\prec$次序将$R_t$中的个体选择至新父代$P_{t+1}$中。具体选择如下：
对于已经排好序的个体，按前沿面顺序整体加入$P_{t+1}$中，也就是${\mathcal{F}}_1$最先加入，然后是${\mathcal{F}}_2$，以此类推；${\mathcal{F}}_i$在加入之前得做一个判断，加入${\mathcal{F}}_i$整个前沿面个体后，是否$P_{t+1}$总数量超过$N$，如果是，则对${\mathcal{F}}_i$中的个体计算拥挤度量，选择最优的个体加入，使得新父代$P_{t+1}$总数量为$N$。

总结

原始论文中给出了详细的实验结果和对比实验

在大多数问题中，实数编码NSGA-II相比其他任何算法，能够找到更好的扩展解——原文

有兴趣的可以查看原文，提供一个[原文中文版翻译链接](https://wenku.baidu.com/view/61daf00d0508763230121235.html

---

最后，再次对前人学者们表示感谢，通过他们的博客与文章使我更好的理解了许多问题，本篇笔记主要参考多目标优化系列（一）NSGA-Ⅱ