tensorflow学习(5)- 用神经网络训练回归问题
前言
上一篇博客:tensorflow学习(4)- 用tensorflow训练线性函数的斜率和截距
这一章解决回归问题。
导入相应包
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
神经网络的层次

这里摘用书上的一张图,最左侧是网络的输入层,在我们的实例中也就是我们用numpy生成的随机样本(x_data,y_data),W表示权重。
准备测试样本
#使用numpy来生成200个随机点,等差数列
x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis]
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data) + noise
Tips:
- [:,np.newaxis]这是给矩阵升维度的,其中逗号前的参数表示升维度的范围,比如[1:5,newaxis]表示原数组中的1到5个成员升维度。
- linspace(-0.5,0.5,200)这个函数第一个参数是起始,第二个是结束,第三个是总数。用于生成等差数列。
设计中间层
#定义神经网络中间层
Weights_L1 = tf.Variable(tf.random_normal([1,10]))
biases_L1 = tf.Variable(tf.zeros([1,10]))
Wx_plus_b_L1 = tf.matmul(x,Weights_L1) + biases_L1
#激活函数
L1 = tf.nn.tanh(Wx_plus_b_L1)
Tips:
- Weights_L1:这是隐藏层第一层的权重,这一层的输入只有x_data一个节点,所以tf.random_normal([1,10])第一参数设成1,然后我们想设计十个神经元,所以把第二个参数设成10。
- biases_L1 :这是偏置的参数,和Weights_L1一样,输入只有一个节点,我们想设计十个神经元的中间层,所以参数设成tf.Variable(tf.zeros([1,10]))
- Wx_plus_b_L1 :这就是上图中a11,a12,a13的结果,输入矩阵乘上权重矩阵加上偏置矩阵。
- L1 = tf.nn.tanh(Wx_plus_b_L1):这是神经网络的核心部分,我们上述所说的输入矩阵乘上权重矩阵加上偏置矩阵这句话可以很显然的知道输出和输入是一个线性的关系,但是在我们的实例中样本是一个二次函数,显然用y = kx+b这样的线是不可能很好的拟合出我们的曲线的,所以这里使用了一个tanh的激活函数,给线性加上非线性的可能。
设计输出层
#定义输出层
Weights_L2 = tf.Variable(tf.random_normal([10,1]))
biases_L2 = tf.Variable(tf.zeros([1,1]))
Wx_plus_b_L2 = tf.matmul(L1,Weights_L2) + biases_L2
#激活函数
prediction = tf.nn.tanh(Wx_plus_b_L2)
Tips:
- Weights_L2:因为我们前文设计了十个神经元的中间层,所以这里的输出层的权重tf.Variable(tf.random_normal([10,1]))第一个参数设成10,然后因为输出只有一个y,所以第二个参数设成1。
- biases_L2 :偏置矩阵的维度设置与权重矩阵相同。
- Wx_plus_b_L2 :输入矩阵乘上权重矩阵加上偏置矩阵。
- prediction = tf.nn.tanh(Wx_plus_b_L2):激活函数含义同前文。
训练
#二次代价函数
loss = tf.reduce_mean(tf.square(y - prediction))
#用梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)
with tf.Session() as sess:
#变量初始化
sess.run(tf.global_variables_initializer())
for i in range(2000):
sess.run(train_step,feed_dict={x:x_data,y:y_data})
#获得预测值
prediction_value = sess.run(prediction,feed_dict = {x:x_data})
#画图
plt.figure()
plt.scatter(x_data,y_data)
plt.plot(x_data,prediction_value,'r-',lw=5)
plt.show()
训练结果
激活函数测试
网上看了很多激活函数的说法,常用的是relu、tanh、sigmoid等。
之所以用这些函数有以下几点考虑:
- 非线性
- 输出范围有限,适合作为输出层
- 输出以0为中心
- 容易计算
- 值不是恒大于零或者恒小于零
- …
初学神经网络,看原理说明实在看的不太明白,这里就尝试下改变几个参数和激活函数看看区别。
使用relu作为激活函数
激活函数:relu
#使用numpy来生成200个随机点,等差数列
x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis]
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data) + noise
#定义两个palceholder
x = tf.placeholder(tf.float32,[None,1])
y = tf.placeholder(tf.float32,[None,1])
#定义神经网络中间层
Weights_L1 = tf.Variable(tf.random_normal([1,10]))
biases_L1 = tf.Variable(tf.zeros([1,10]))
Wx_plus_b_L1 = tf.matmul(x,Weights_L1) + biases_L1
#激活函数
L1 = tf.nn.relu(Wx_plus_b_L1)
#定义输出层
Weights_L2 = tf.Variable(tf.random_normal([10,1]))
biases_L2 = tf.Variable(tf.zeros([1,1]))
Wx_plus_b_L2 = tf.matmul(L1,Weights_L2) + biases_L2
#激活函数
prediction = tf.nn.relu(Wx_plus_b_L2)
#二次代价函数
loss = tf.reduce_mean(tf.square(y - prediction))
#用梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)#修改学习率!!!
with tf.Session() as sess:
#变量初始化
sess.run(tf.global_variables_initializer())
for i in range(2000):
sess.run(train_step,feed_dict={x:x_data,y:y_data})
#获得预测值
prediction_value = sess.run(prediction,feed_dict = {x:x_data})
#画图
plt.figure()
plt.scatter(x_data,y_data)
plt.plot(x_data,prediction_value,'r-',lw=5)
plt.show()
输出结果
学习率:0.04

学习率:0.1

学习率:0.2
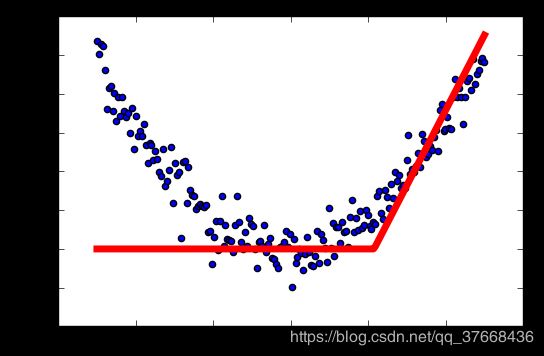
学习率:0.3
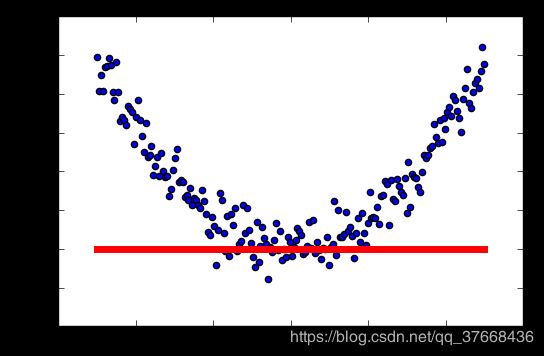
学习率:0.4

学习率:0.5
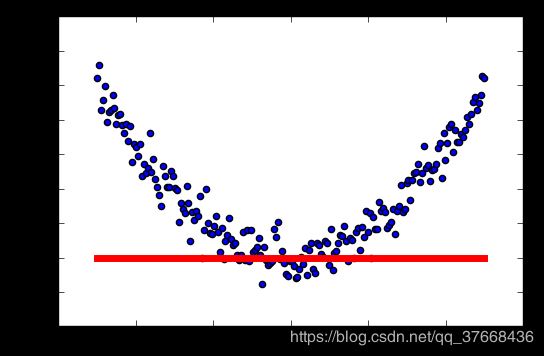
学习率:0.6
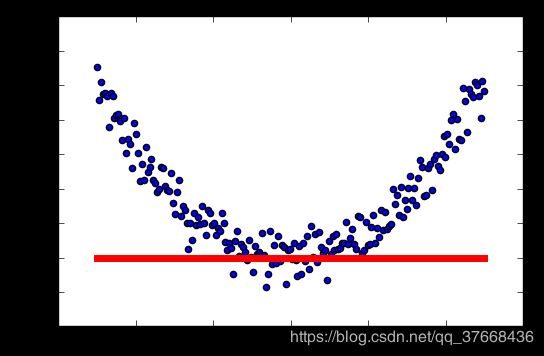
relu总结
学习率越高,激活越容易失败。
这里不是很严谨,样本是随机生成的,每次生成不一样,没有做到控制变量…但大概能看出学习率对relu激活函数的影响。
使用tanh作为激活函数
#使用numpy来生成200个随机点,等差数列
x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis]
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data) + noise
#定义两个palceholder
x = tf.placeholder(tf.float32,[None,1])
y = tf.placeholder(tf.float32,[None,1])
#定义神经网络中间层
Weights_L1 = tf.Variable(tf.random_normal([1,10]))
biases_L1 = tf.Variable(tf.zeros([1,10]))
Wx_plus_b_L1 = tf.matmul(x,Weights_L1) + biases_L1
#激活函数
L1 = tf.nn.tanh(Wx_plus_b_L1)
#定义输出层
Weights_L2 = tf.Variable(tf.random_normal([10,1]))
biases_L2 = tf.Variable(tf.zeros([1,1]))
Wx_plus_b_L2 = tf.matmul(L1,Weights_L2) + biases_L2
#激活函数
prediction = tf.nn.tanh(Wx_plus_b_L2)
#二次代价函数
loss = tf.reduce_mean(tf.square(y - prediction))
#用梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.04).minimize(loss)
with tf.Session() as sess:
#变量初始化
sess.run(tf.global_variables_initializer())
for i in range(2000):
sess.run(train_step,feed_dict={x:x_data,y:y_data})
#获得预测值
prediction_value = sess.run(prediction,feed_dict = {x:x_data})
#画图
plt.figure()
plt.scatter(x_data,y_data)
plt.plot(x_data,prediction_value,'r-',lw=5)
plt.show()
输出结果
学习率:0.01
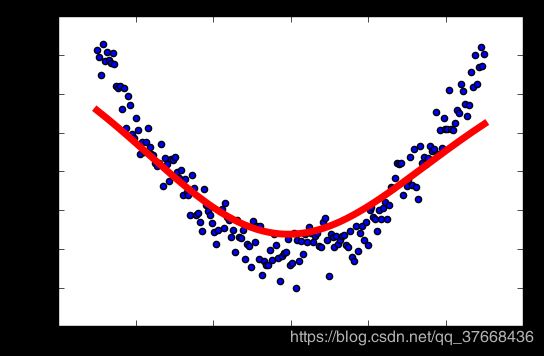
学习率:0.04

学习率:0.1
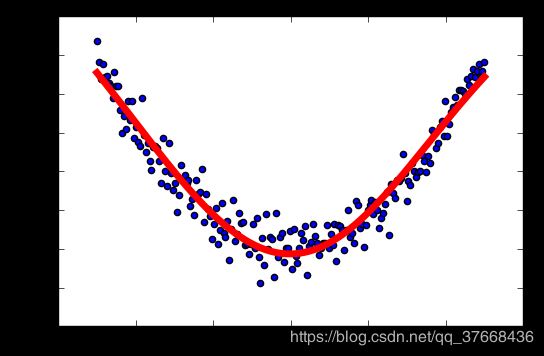
学习率:0.2
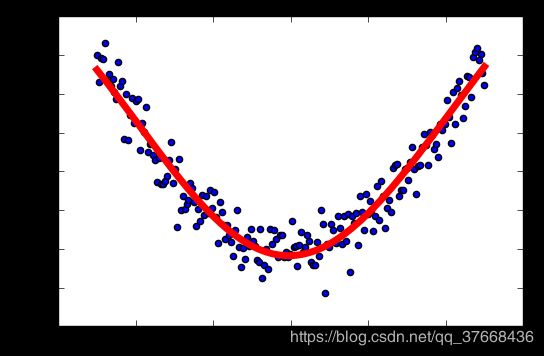
学习率:0.3

学习率:0.4
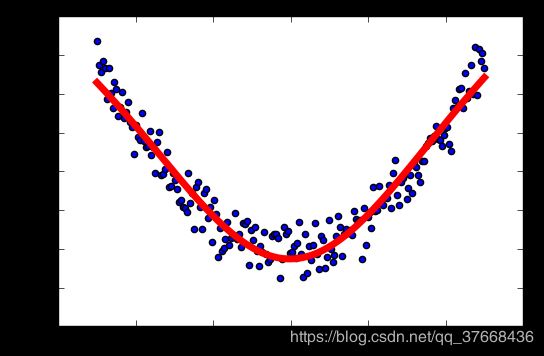
学习率:0.5
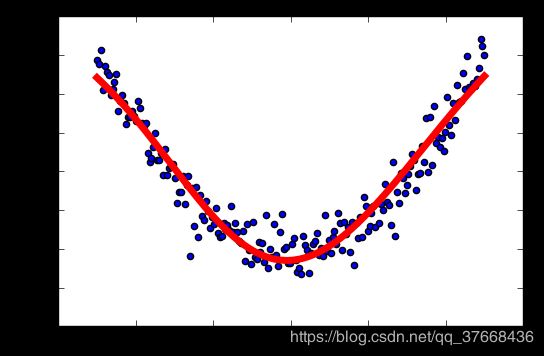
学习率:0.6
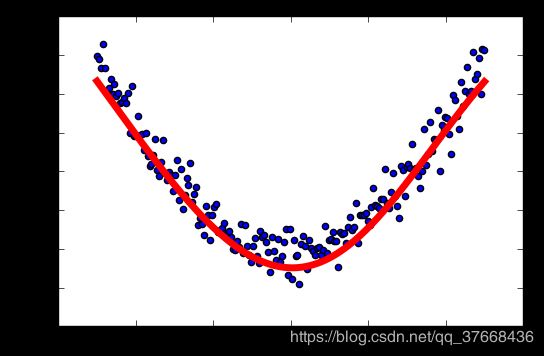
总结
学习率过低的话,结果不准确
使用sigmoid作为激活函数
#使用numpy来生成200个随机点,等差数列
x_data = np.linspace(-0.5,0.5,200)[:,np.newaxis]
noise = np.random.normal(0,0.02,x_data.shape)
y_data = np.square(x_data) + noise
#定义两个palceholder
x = tf.placeholder(tf.float32,[None,1])
y = tf.placeholder(tf.float32,[None,1])
#定义神经网络中间层
Weights_L1 = tf.Variable(tf.random_normal([1,10]))
biases_L1 = tf.Variable(tf.zeros([1,10]))
Wx_plus_b_L1 = tf.matmul(x,Weights_L1) + biases_L1
#激活函数
L1 = tf.nn.sigmoid(Wx_plus_b_L1)
#定义输出层
Weights_L2 = tf.Variable(tf.random_normal([10,1]))
biases_L2 = tf.Variable(tf.zeros([1,1]))
Wx_plus_b_L2 = tf.matmul(L1,Weights_L2) + biases_L2
#激活函数
prediction = tf.nn.sigmoid(Wx_plus_b_L2)
#二次代价函数
loss = tf.reduce_mean(tf.square(y - prediction))
#用梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.04).minimize(loss)
with tf.Session() as sess:
#变量初始化
sess.run(tf.global_variables_initializer())
for i in range(2000):
sess.run(train_step,feed_dict={x:x_data,y:y_data})
#获得预测值
prediction_value = sess.run(prediction,feed_dict = {x:x_data})
#画图
plt.figure()
plt.scatter(x_data,y_data)
plt.plot(x_data,prediction_value,'r-',lw=5)
plt.show()
输出结果
学习率:0.04
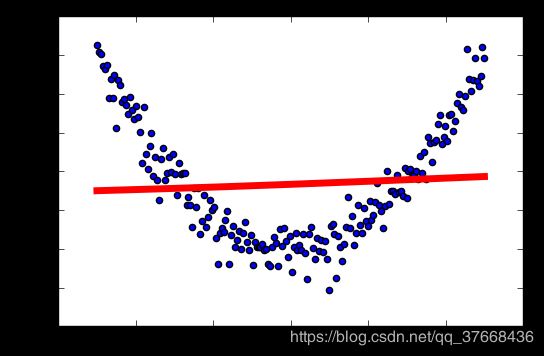
学习率:0.1
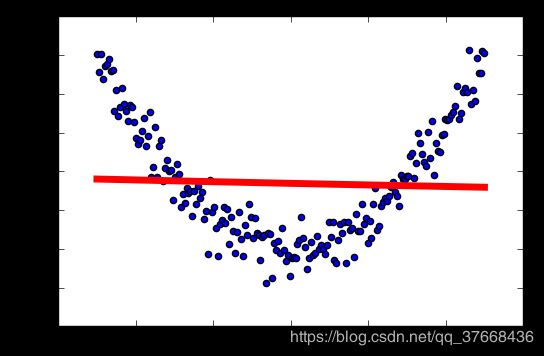
学习率:0.2
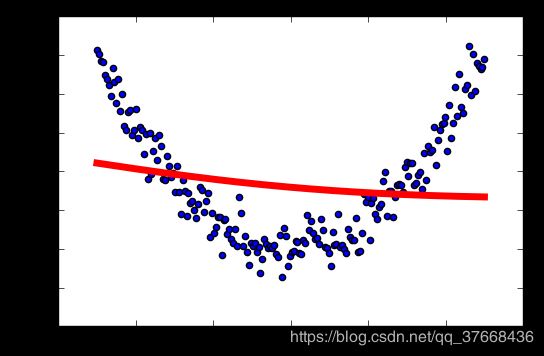
学习率:0.3
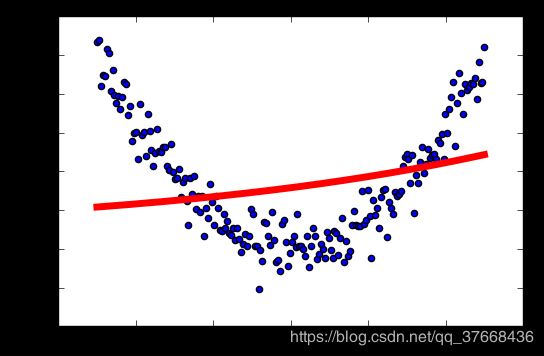
学习率:0.4

学习率:0.5
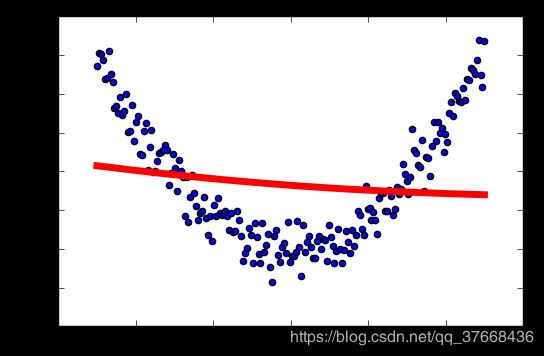
学习率:0.6
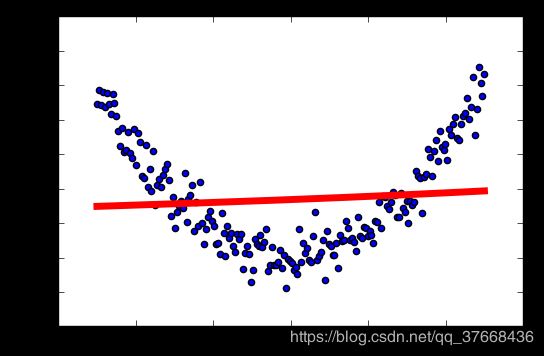
总结
这个显然不合适作为我们这个模型的激活函数。
