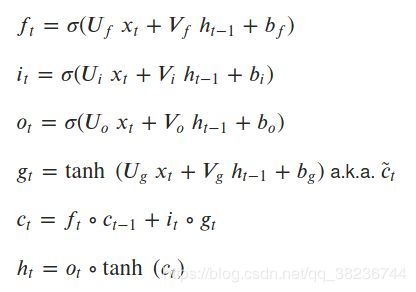LSTM:从原理理解开始使用pytorch构建网络
这是一个造轮子的过程,但是从头构建LSTM能够使我们对体系结构进行更加了解,并将我们的研究带入下一个层次。
LSTM单元是递归神经网络深度学习研究领域中最有趣的结构之一:它不仅使模型能够从长序列中学习,而且还为长、短期记忆创建了一个数值抽象,可以在需要时相互替换。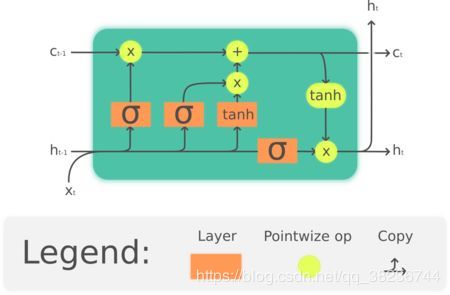
在这篇文章中,我们不仅将介绍LSTM单元的体系结构,还将通过PyTorch手工实现它。
最后但最不重要的是,我们将展示如何对我们的实现做一些小的调整,以实现一些新的想法,这些想法确实出现在LSTM研究领域,如peephole。
-
LSTM体系结构
LSTM被称为门结构:一些数学运算的组合,这些运算使信息流动或从计算图的那里保留下来。因此,它能够“决定”其长期和短期记忆,并输出对序列数据的可靠预测:
 LSTM单元中的预测序列。注意,它不仅会传递预测值,而且还会传递一个c,c是长期记忆的代表。
LSTM单元中的预测序列。注意,它不仅会传递预测值,而且还会传递一个c,c是长期记忆的代表。 -
遗忘门
遗忘门(forget gate)是输入信息与候选者一起操作的门,作为长期记忆。请注意,在输入、隐藏状态和偏差的第一个线性组合上,应用一个sigmoid函数: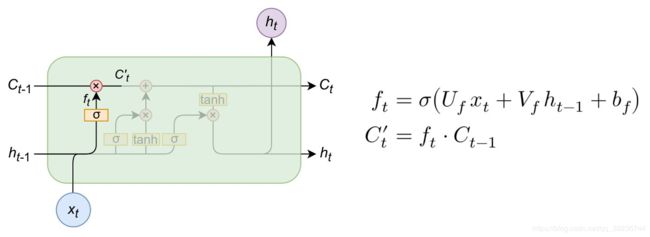 sigmoid将遗忘门的输出“缩放”到0-1之间,然后,通过将其与候选者相乘,我们可以将其设置为0,表示长期记忆中的“遗忘”,或者将其设置为更大的数字,表示我们从长期记忆中记住的“多少”。
sigmoid将遗忘门的输出“缩放”到0-1之间,然后,通过将其与候选者相乘,我们可以将其设置为0,表示长期记忆中的“遗忘”,或者将其设置为更大的数字,表示我们从长期记忆中记住的“多少”。 -
新型长时记忆的输入门及其解决方案
输入门是将包含在输入和隐藏状态中的信息组合起来,然后与候选和部分候选c’'u t一起操作的地方: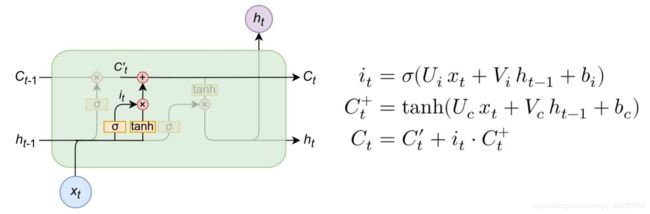 在这些操作中,决定了多少新信息将被引入到内存中,如何改变——这就是为什么我们使用tanh函数(从-1到1)。我们将短期记忆和长期记忆中的部分候选组合起来,并将其设置为候选。
在这些操作中,决定了多少新信息将被引入到内存中,如何改变——这就是为什么我们使用tanh函数(从-1到1)。我们将短期记忆和长期记忆中的部分候选组合起来,并将其设置为候选。 -
单元的输出门和隐藏状态(输出)
之后,我们可以收集o_t作为LSTM单元的输出门,然后将其乘以候选单元(长期存储器)的tanh,后者已经用正确的操作进行了更新。网络输出为h_t。
-
pytorch custom LSTM
-
精简版:
构造函数:想要了解每个操作的形状,1. 矩阵的输入形状是(批量大小、序列长度、特征长度),因此将序列的每个元素相乘的权重矩阵必须具有该形状(特征长度、输出长度);2. 序列上每个元素的隐藏状态(也称为输出)都具有形状(批大小、输出大小),这将在序列处理结束时产生输出形状(批大小、序列长度、输出大小)。-因此,将其相乘的权重矩阵必须具有与单元格的参数hiddensz相对应的形状(outputsize,output_size)。代码如下:class NaiveCustomLSTM(nn.Module): def __init__(self, input_sz: int, hidden_sz: int): super().__init__() # 一般数据输入为[bs, suq_size, feature_size] # 输入每个tokenize的size(即每个词向量编码长度) self.input_size = input_sz # 隐层每个tokenize的size self.hidden_size = hidden_sz # i_t self.W_i = nn.Parameter(torch.Tensor(input_sz, hidden_sz)) self.U_i = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz)) self.b_i = nn.Parameter(torch.Tensor(hidden_sz)) # f_t self.W_f = nn.Parameter(torch.Tensor(input_sz, hidden_sz)) self.U_f = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz)) self.b_f = nn.Parameter(torch.Tensor(hidden_sz)) # c_t self.W_c = nn.Parameter(torch.Tensor(input_sz, hidden_sz)) self.U_c = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz)) self.b_c = nn.Parameter(torch.Tensor(hidden_sz)) # o_t self.W_o = nn.Parameter(torch.Tensor(input_sz, hidden_sz)) self.U_o = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz)) self.b_o = nn.Parameter(torch.Tensor(hidden_sz)) self.init_weights() def init_weights(self): """ 权重与偏置初始化 :return: """ stdv = 1.0 / math.sqrt(self.hidden_size) for weight in self.parameters(): weight.data.uniform_(-stdv, stdv) def forward(self, x, init_states=None): """assumes x.shape represents (batch_size, sequence_size, input_size) input: 前馈操作接收init_states参数,该参数是上面方程的(h_t, c_t)参数的元组, 如果不引入,则设置为零。然后,我们对每个保留(h_t, c_t)的序列元素执行LSTM方程的前馈, 并将其作为序列下一个元素的状态引入. return: 预测和最后一个状态元组 """ bs, seq_sz, _ = x.size() hidden_seq = [] if init_states is None: # 初始化历史状态 h_t, c_t = ( torch.zeros(bs, self.hidden_size).to(x.device), torch.zeros(bs, self.hidden_size).to(x.device), ) else: h_t, c_t = init_states for t in range(seq_sz): # 获取单个词的feature 向量 x_t = x[:, t, :] i_t = torch.sigmoid(x_t @ self.W_i + h_t @ self.U_i + self.b_i) f_t = torch.sigmoid(x_t @ self.W_f + h_t @ self.U_f + self.b_f) g_t = torch.tanh(x_t @ self.W_c + h_t @ self.U_c + self.b_c) o_t = torch.sigmoid(x_t @ self.W_o + h_t @ self.U_o + self.b_o) c_t = f_t * c_t + i_t * g_t h_t = o_t * torch.tanh(c_t) hidden_seq.append(h_t.unsqueeze(0)) # reshape hidden_seq p/ retornar hidden_seq = torch.cat(hidden_seq, dim=0) hidden_seq = hidden_seq.transpose(0, 1).contiguous() return hidden_seq, (h_t, c_t) -
优化版: Naive LSTM在运算上是正确的,但在计算时间上没有进行优化:我们分别执行8个矩阵乘法,这比矢量化的方式慢得多。我们现在将演示如何通过将其减少到2个矩阵乘法来完成,这将使它更快。
为此,我们设置了两个矩阵U和V,它们的权重包含在4个矩阵乘法上。然后,我们对已经通过线性组合+偏置操作的矩阵执行选通操作。

class CustomLSTM(nn.Module): def __init__(self, input_sz, hidden_sz): super().__init__() # 一般数据输入为[bs, suq_size, feature_size] # 输入每个tokenize的size(即每个词向量编码长度) self.input_size = input_sz # 隐层每个tokenize的size self.hidden_size = hidden_sz self.W = nn.Parameter(torch.Tensor(input_sz, hidden_sz * 4)) self.U = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz * 4)) self.bias = nn.Parameter(torch.Tensor(hidden_sz * 4)) self.init_weights() def init_weights(self): """ 权重与偏置初始化 :return: """ stdv = 1.0 / math.sqrt(self.hidden_size) for weight in self.parameters(): weight.data.uniform_(-stdv, stdv) def forward(self, x, init_states=None): """assumes x.shape represents (batch_size, sequence_size, input_size) input: 前馈操作接收init_states参数,该参数是上面方程的(h_t, c_t)参数的元组, 如果不引入,则设置为零。然后,我们对每个保留(h_t, c_t)的序列元素执行LSTM方程的前馈, 并将其作为序列下一个元素的状态引入. return: 预测和最后一个状态元组 """ bs, seq_sz, _ = x.size() hidden_seq = [] if init_states is None: # 初始化历史状态 h_t, c_t = ( torch.zeros(bs, self.hidden_size).to(x.device), torch.zeros(bs, self.hidden_size).to(x.device), ) else: h_t, c_t = init_states HS = self.hidden_size for t in range(seq_sz): # 获取单个词的feature 向量 x_t = x[:, t, :] # batch the computations into a single matrix multiplication gate = x_t @ self.W + h_t @ self.U + self.bias i_t, f_t, g_t, o_t = ( torch.sigmoid(gate[:, :HS]), # input torch.sigmoid(gate[:, HS:HS*2]), # forget torch.tanh(gate[:, HS*2:HS*3]), torch.sigmoid(gate[:, HS*3:]), # output ) c_t = f_t * c_t + i_t * g_t h_t = o_t * torch.tanh(c_t) hidden_seq.append(h_t.unsqueeze(0)) # reshape hidden_seq p/ retornar hidden_seq = torch.cat(hidden_seq, dim=0) # reshape from shape (sequence, batch, feature) to (batch, sequence, feature) hidden_seq = hidden_seq.transpose(0, 1).contiguous() return hidden_seq, (h_t, c_t) -
LSTM peephole: 对前馈操作进行了细微调整,从而将其更改为优化的情况:
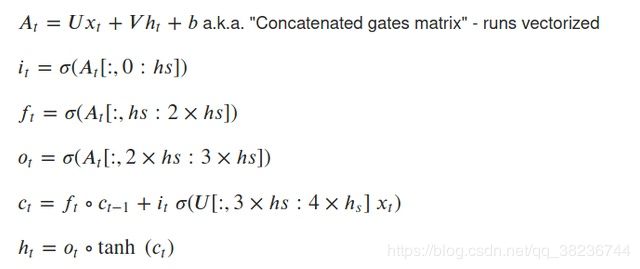
class CustomLSTMPeephole(nn.Module): def __init__(self, input_sz, hidden_sz, peephole=False): super().__init__() # 一般数据输入为[bs, suq_size, feature_size] # 输入每个tokenize的size(即每个词向量编码长度) self.input_size = input_sz # 隐层每个tokenize的size self.hidden_size = hidden_sz self.peephole = peephole self.W = nn.Parameter(torch.Tensor(input_sz, hidden_sz * 4)) self.U = nn.Parameter(torch.Tensor(hidden_sz, hidden_sz * 4)) self.bias = nn.Parameter(torch.Tensor(hidden_sz * 4)) self.init_weights() def init_weights(self): """ 权重与偏置初始化 :return: """ stdv = 1.0 / math.sqrt(self.hidden_size) for weight in self.parameters(): weight.data.uniform_(-stdv, stdv) def forward(self, x, init_states=None): """assumes x.shape represents (batch_size, sequence_size, input_size) input: 前馈操作接收init_states参数,该参数是上面方程的(h_t, c_t)参数的元组, 如果不引入,则设置为零。然后,我们对每个保留(h_t, c_t)的序列元素执行LSTM方程的前馈, 并将其作为序列下一个元素的状态引入. return: 预测和最后一个状态元组 """ bs, seq_sz, _ = x.size() hidden_seq = [] if init_states is None: # 初始化历史状态 h_t, c_t = ( torch.zeros(bs, self.hidden_size).to(x.device), torch.zeros(bs, self.hidden_size).to(x.device), ) else: h_t, c_t = init_states HS = self.hidden_size for t in range(seq_sz): # 获取单个词的feature 向量 x_t = x[:, t, :] # batch the computations into a single matrix multiplication if self.peephole: gate = x_t @ self.W + h_t @ self.U + self.bias else: gate = x_t @ self.W + h_t @ self.U + self.bias g_t = torch.tanh(gate[:, HS*2:HS*3]) i_t, f_t, o_t = ( torch.sigmoid(gate[:, :HS]), # input torch.sigmoid(gate[:, HS:HS*2]), # forget torch.sigmoid(gate[:, HS*3:]), # output ) if self.peephole: c_t = f_t * c_t + i_t * torch.sigmoid(x_t @ self.W + self.bias)[:, HS*2:HS*3] h_t = torch.tanh(o_t * c_t) else: c_t = f_t * c_t + i_t * g_t h_t = o_t * torch.tanh(c_t) hidden_seq.append(h_t.unsqueeze(0)) # reshape hidden_seq p/ retornar hidden_seq = torch.cat(hidden_seq, dim=0) # reshape from shape (sequence, batch, feature) to (batch, sequence, feature) hidden_seq = hidden_seq.transpose(0, 1).contiguous() return hidden_seq, (h_t, c_t)
-
代码实现github地址:https://github.com/QiuSYang/DeepLearningStudy_YQS/tree/master/basic_network/lstm
Reference:
- https://zhuanlan.zhihu.com/p/144132609
- https://github.com/piEsposito/pytorch-lstm-by-hand