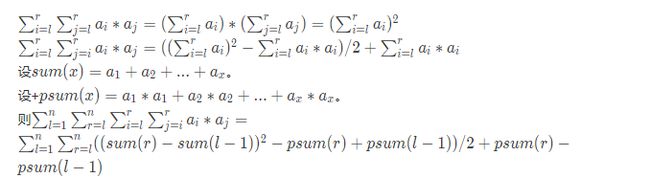牛客练习赛64 A-D题解
A.怪盗-1412
题目地址
A.怪盗-1412
题意简述
一个长度为n+m+k包含n个数字1,m个数字2和k个数字4的数组,最多可能有多少个1412子序列?
题解
由于2和4在1412中出现的次数都是1次,所以不需要考虑将连续的4或者是连续的2分开的情况
就比如
1444412
没必要写成
4414412
很明显会出现4的浪费
因为子序列的相对位置是不能改变的
那么我们实际上需要考虑的就是1的情况,
设开头的1有 x x x个,在4和2之间的1就会有 n − x n-x n−x个
最多子序列即求解 ( n − x ) ∗ x (n - x) * x (n−x)∗x
即相当于求解二次函数最大值
y = ( n ∗ n ) / 4 y = (n * n) / 4 y=(n∗n)/4
所以序列的组成是这样的
x个1 k个4 n-x个1 m个2
第一个1我们可以从第一部分取C1x,x个中取一个作为第一个
第二个4我们从第二个部分取C1K,往后同理
于是最后的结果
ans=(n * n)/4 * k*m
代码
int main(){
int t; RD(t);
while(t--){
LL n, m, k; RDD(n, m, k);
if (n == 1) {
printf("0\n");
}
else {
LL ans = m * ((n * n) / 4) * k;
OT(ans);
}
}
}
B. Dis2
题目地址
B.Dis2
题意简述
给你树的连接,要你求解每个节点所连接的距离为2的节点有多少个?
-
样例输入
4
1 2
2 3
3 4 -
样例输出
1
1
1
1
点{1,3}的距离为2,点{2,4}的距离为2。
题解
每个遍历每个节点(1)所连接的节点(2),通过节点(2)的大小能很清楚计算出与节点(1)距离为2的点有多少个,但要注意节点(1)连接着节点(2),同时节点(2)也连接着节点(1),所以在计算节点(2)的大小的时候需要注意减1
代码
typedef vector<int> VI;
const int maxn = 2e6 + 50;
VI G[maxn];
int main(){
int n; RD(n);
int u, v;
REP(i, n - 1){
RD(u, v);
G[u].PB(v);
G[v].PB(u);
}
FOR_1(i, 1, n){
LL ans = 0;
for(int v: G[i]){
ans += G[v].size() - 1;
}
cout << ans << '\n';
}
}
C.序列卷积之和
题目地址
C.序列卷积之和
题意简述
求解 ∑ l = 1 n ∑ r = l n ∑ i = l r ∑ j = i r a i ∗ a j \sum_{l=1}^{n}\sum_{r=l}^{n}\sum_{i=l}^{r}\sum_{j=i}^{r}a_i*a_j ∑l=1n∑r=ln∑i=lr∑j=irai∗ajmod 1 e 9 + 7 1e9+7 1e9+7
题解
预处理前缀和统计前缀和出现的数量。
n = 2
a[1] * a[1] + a[1] * a[1] + a[1] * a[2] + a[2] * a[2] + a[2] * a[2]
n = 3
a[1] * a[1] + a[1] * a[1] + a[1] * a[2] + a[2] * a[2] + a[1] * a[1] + a[1] * a[2] + a[1] * a[3] + a[2] * a[2] + a[2] * a[3] + a[3] * a[3] + a[2] * a[2] + a[2] * a[2] + a[2] * a[3] + a[3] * a[3] + a[3] * a[3]
//附打印程序
int main(){
int n; cin >> n;
for(int l = 1; l <= n; l++) {
for(int r = l; r <= n; r++) {
for(int i = l; i <= r; i++) {
for(int j = i; j <= r; j++){
cout << "a" << "[" << i << "]" << " * " << "a" << "[" << j << "]" << " + ";
}
}
}
}
}
可以很清楚的看到n = 2和 n = 3有那么一些相似之处
n = 2有的n = 3都有
在n=2中 a i 2 a_i^2 ai2出现都是两次
类推,
易知 a i a_i ai只与 i i i存在关系,同理 a j a_j aj只与 j j j存在关系,所以可以分开考虑
∑ i = l r ∑ j = l r a i ∗ a j = ( ∑ i = l r a i ) ∗ ( ∑ j = l r a j ) \sum_{i=l}^r\sum_{j=l}^ra_i * a_j = (\sum_{i=l}^ra_i)*(\sum_{j=l}^ra_j) ∑i=lr∑j=lrai∗aj=(∑i=lrai)∗(∑j=lraj)
再看一眼n=2的时候的情况
a[1] * a[1] + a[1] * a[1] + a[1] * a[2] + a[2] * a[2] + a[2] * a[2]
其实可以化简成
2 ∗ a [ 1 ] 2 + a [ 1 ] ∗ a [ 2 ] + 2 ∗ a [ 2 ] 2 2*a[1]^2+a[1]*a[2]+2*a[2]^2 2∗a[1]2+a[1]∗a[2]+2∗a[2]2
以此去想
( ∑ i = l r a i ) ∗ ( ∑ j = l r a j ) = ( ( ∑ i = l r a i ) 2 − ∑ i = l r a i ∗ a i ) / 2 + ∑ i = l r a i ∗ a i (\sum_{i=l}^ra_i)*(\sum_{j=l}^ra_j) = ((\sum_{i=l}^ra_i)^2-\sum_{i=l}^ra_i * a_i)/2+\sum_{i=l}^ra_i * a_i (∑i=lrai)∗(∑j=lraj)=((∑i=lrai)2−∑i=lrai∗ai)/2+∑i=lrai∗ai
外层还有两个循环,类似推断
代码
const int maxn = 2e5+60;
LL a[maxn], s[maxn], s2[maxn],ans = 0;
const int mod = 1e9 + 7;
int main(){
int n; RD(n);
FOR_1(i, 1, n) cin >> a[i];
FOR_1(i, 1, n) s[i] = (s[i - 1] + a[i]) % mod;
FOR_1(i, 1, n) s2[i] = (s2[i - 1] + s[i]) % mod;
FOR_1(i, 1, n)
{
ans += i * a[i] % mod * ((s2[n] - s2[i-1] + mod) % mod - (n - i + 1) * s[i-1] % mod + mod) % mod;
ans %= mod;
}
cout << ans << endl;
}
D.宝石装箱
题目地址
D.宝石装箱
题意简述
n n n颗宝石装进 n n n个箱子使得每个箱子中都有一颗宝石。第 i i i颗宝石不能装入第 a i a_i ai个箱子。求合法的装箱方案对 998244353 998244353 998244353取模。
(两种装箱方案不同当且仅当两种方案中存在一颗编号相同的宝石装在不同编号的箱子中。)
- 输入样例
2
1 2 - 输出样例
1
题解
容斥+dp
- 在不考虑不符合情况时,总的方案数allnum
a l l n u m = n ! = n ∗ ( n − 1 ) ∗ ( n − 2 ) ∗ . . . ∗ ( 1 ) allnum = n! = n * (n - 1) * (n - 2) * ... * ( 1 ) allnum=n!=n∗(n−1)∗(n−2)∗...∗(1) - 合法方案数实际上就是等于总的方案数 减去 不合法方案数
a n s = a l l n u m − u n n u m ans = allnum - unnum ans=allnum−unnum - 设函数 f ( x ) f(x) f(x)表示x箱子中不合法的方案数
- 设 d p [ i ] [ j ] dp[i][j] dp[i][j]表示前 i i i个箱子中,存在j个不合法的方案数
- 这里运用dp,要注意,你所计算的是方案数,而不是背包问题中的重量或者是权重什么的
d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i − 1 ] [ j − 1 ] ∗ a [ i ] dp[i][j]=dp[i-1][j]+dp[i-1][j-1] * a[i] dp[i][j]=dp[i−1][j]+dp[i−1][j−1]∗a[i]
在前i个箱子中有j个不合法方案数,可能是由于前i-1个箱子中就有j个不合法方案数,也有可能是第i个箱子才有j个不合法方案数,所以是
d p [ i − 1 ] [ j ] + d p [ i − 1 ] [ j − 1 ] ∗ a [ i ] dp[i-1][j]+dp[i-1][j-1] * a[i] dp[i−1][j]+dp[i−1][j−1]∗a[i]
至少i个箱子装了不合法的宝石的方案数 = d p [ n ] [ i ] ∗ ( n − i ) ! = dp[n][i] * (n - i)! =dp[n][i]∗(n−i)!

根据容斥,可得
n ! − ∑ i = 1 n ∗ ( − 1 ) i ∗ d p [ n ] [ i ] ∗ ( n − i ) ! n!-\sum_{i=1}^n*(-1)^i*dp[n][i]*(n-i)! n!−∑i=1n∗(−1)i∗dp[n][i]∗(n−i)!
∑ i = 0 n ∗ ( − 1 ) i ∗ d p [ n ] [ i ] ∗ ( n − i ) ! \sum_{i=0}^n*(-1)^i*dp[n][i]*(n-i)! ∑i=0n∗(−1)i∗dp[n][i]∗(n−i)!
代码
const int maxn = 1e4+50;
LL dp[maxn], fact[maxn];
LL a[maxn];
const LL mod = 998244353;
void init(){
memset(a, 0, sizeof a);
fact[0] = 1;
FOR_1(i, 1, maxn - 1){
fact[i] = fact[i - 1] * i % mod;
}
}
int main(){
init();
int n; cin >> n;
FOR_1(i, 1, n){
LL x; RDD(x); a[x]++;;
}
dp[0] = 1;
FOR_1(i, 1, n){
for(int j = i; j >= 1; j--){
(dp[j] += dp[j - 1] * a[i]) %= mod;
}
}
LL ans = 0;
dp[0] = 1;
FOR_1( i, 0, n){
if (i & 1) ans -= dp[i] * fact[n - i];
else ans += dp[i] * fact[n - i];
ans = (ans + mod) % mod;
}
ans %= mod;
cout << ans << '\n';
}
case通过率为%13.3可以考虑一下是不是爆int的问题