【Nowcode】2020牛客暑期多校训练营（第五场）B-graph | 最小异或生成树、字典树、分治

题目大意：

给你一棵树，你可以删除一些边或者增加一些边，但是在过程中必须保证图联通并且出现的任何一个

环的边权异或和为0，最后的图还是一个树，使得图中的所有边的权值之和最小。

解题思路：

题目说可以增加或删除一些边，不如先把没有给出的边的边权全部求出来，使得此图变为完全图，然

后在这个完全图上做文章。

首先要明确这个完全图的所有边的边权是不是唯一的，答案是唯一的，给你的这棵树的每条边的边权

都是已经确定的，没给的边都可以与已有的边构成环，题目中已经强调出现的任何一个环的边权异或

和为0。设一条未知的边的边权为x，与它构成环的其他已知边的边权为a,b,c。由题意得x==a ^ b ^ c，

所以x的值是确定的，所以某一未知边的权值就等于从一个根节点到这个点的边权的异或和，由此我们

不难发现，可以构造一组点值，使得节点u、v的边权等于节点v的点值^节点u的点值。构造并不难，看

下图：

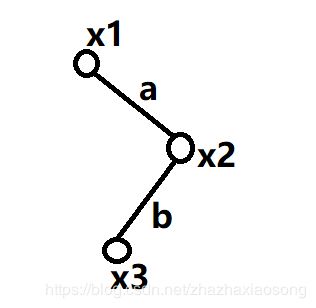
可以任选一个根节点，使其点值为0，用p来代表某一个点的点值，假设p[x1]=0，则p[x2]=0^a，

p[x3]=0 ^ a ^ b，由x ^ y = z可以得到x ^ z = y，所以 a = p[x1] ^ p[x2] = a，b = p[x2] ^ p[x3] = b，点x1

与点x3连线的边权就等于a ^ b,正好满足题意，接下来就是跑一下最小异或生成树了，如果最小异或生

成树不太懂，可以参考一下这个博客

Code：

#include
#include
#include
#include
#include
#include
using namespace std;
const int maxn = 3000010;
const int mod = 1e9+9;
typedef long long ll;
typedef pair<int,int> PII;
int n,m,k;
int tot;
ll a[maxn];
int h[maxn],e[maxn],ne[maxn],w[maxn],idx;
int l[maxn],r[maxn];
int tr[maxn][2];
inline bool read(ll &num)
{char in;bool IsN=false;
in=getchar();if(in==EOF) return false;while(in!='-'&&(in<'0'||in>'9')) in=getchar();if(in=='-'){ IsN=true;num=0;}else num=in-'0';while(in=getchar(),in>='0'&&in<='9'){num*=10,num+=in-'0';}if(IsN) num=-num;return true;}
void add(int a,int b,int c){
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int fa,ll c){
    a[u]=c;
    for(int i=h[u];i!=-1;i=ne[i]){
        int j=e[i];
        if(j==fa) continue;
        dfs(j,u,c^w[i]);
    }
}
void Insert(ll x,int id){
    int p=0;
    for(int i=32;i>=0;i--){
        int u = x>>i&1;
        if(!tr[p][u]) tr[p][u] = ++tot;
        p=tr[p][u];
        if(!l[p]) l[p] = id;
        r[p] = id;
    }
}
ll AC(int p,int pos,ll x){
    ll res=0;
    for(int i=pos;i>=0;i--)
    {
        int u = x>>i&1;
        if(tr[p][u]) p=tr[p][u];
        else {
            res+=(1<<i);
            p=tr[p][!u];
        }
    }
    return res;
}
ll query(int p,int pos){
    if(tr[p][0] && tr[p][1]){
        int x = tr[p][0],y = tr[p][1];
        ll minn=1e17;
        for(int i=l[x];i<=r[x];i++) minn=min(minn,AC(y,pos-1,a[i])+(1<<pos));
        return minn+query(tr[p][0],pos-1)+query(tr[p][1],pos-1);
    }
    else if(tr[p][0]) return query(tr[p][0],pos-1);
    else if(tr[p][1]) return query(tr[p][1],pos-1);
    return 0;
}
int main(){
    scanf("%d",&n);
    memset(h,-1,sizeof h);
    for(int i=1;i<n;i++)
    {
        int a,b,c;scanf("%d%d%d",&a,&b,&c);
        a++,b++;
        add(a,b,c);
        add(b,a,c);
    }
    dfs(1,1,0);
    ///for(int i=1;i<=n;i++) cout << a[i] << " ";
    ///puts("");
    sort(a+1,a+1+n);
    for(int i=1;i<=n;i++) Insert(a[i],i);
    printf("%lld\n",query(0,32));
    return 0;
}

白云从不向天空承诺守候却朝夕相伴；风景从不向眼睛说出永恒却始终美丽；星星从不向黑夜许诺光

明却努力闪烁；朋友从不向对方倾诉思念却永远牵挂。