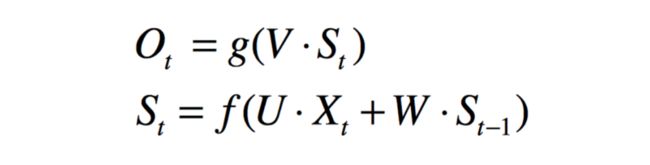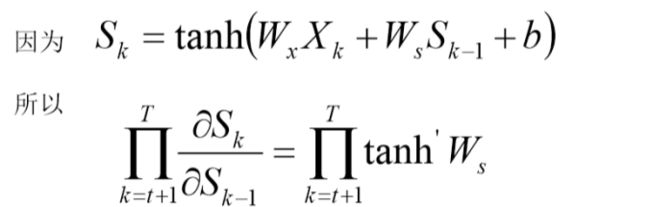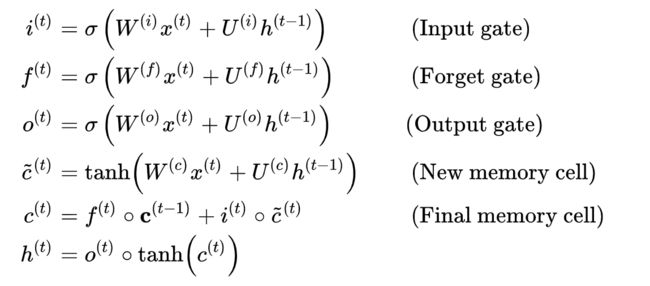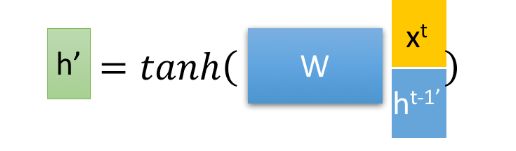干货!RNN、LSTM、GRU学习笔记
为什么需要RNN?
我们的神经网络是一个可解释性很差的黑盒子,给定足够的数据,它就能最大程度拟合出这个网络中的各个参数,这样当你给定一个它没有遇见过从输入时,它能大概率的输出一个很接近实际输出的结果。但是在RNN之前,我们的神经网络只能单独地处理一个个的输入,前一个输入和后一个 输入是完全没有关系的,但如果是要处理前后输入有关系的序列信息,就需要一个更加专能的网络来担此重任了。于是RNN(循环神经网络,Recurrent Neural Network)就出来了,它被提出来就是为了更好的处理序列信息的。
RNN基本结构
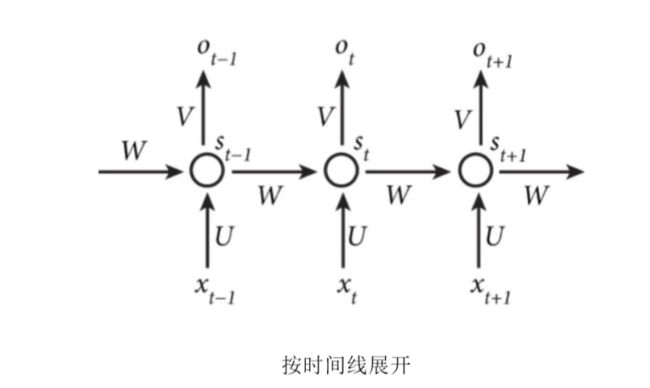
RNN 由输入层、隐藏层和输出层组成,U是输入层到隐藏层的权重矩阵,V是隐藏层到输出层的权重矩阵,S是一个向量,它表示隐藏层的值,O是一个向量,它表示输出层的值。RNN的循环就是体现在隐藏层的循环中,可以发现如果没有W的部分,那么网络就退化成了一个普通的全连接神经网络。
将上面的网络按时间线展开:
可以看到t时刻的输出O(t)由上一时刻的状态S(t-1)和当前时刻的输入x(t)决定。用公式表示:
RNN在每个阶段都共享一个参数W,隐藏层激活函数通常采用tanh;在反向传播的时候,我们需要计算U,V,W等参数的梯度,对T时刻的W进行梯度计算:
那么T时刻W的梯度就成啥了呢,放在一起看的更明晰:
由此可知RNN的反向传播是与时间序列有关系的,我们以此来表征序列信息中的前后关系,这样就能初步解决我们之前全连接神经网络无法处理序列信息(例如语句文本、音视频信息等)的问题了。
RNN的问题
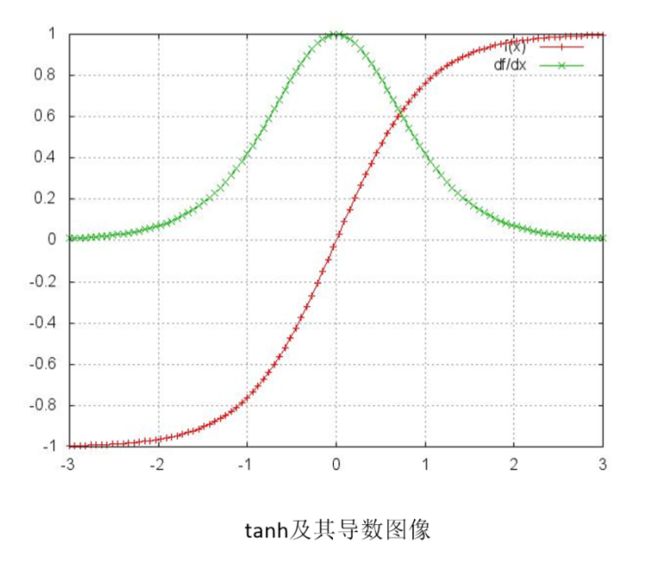
根据上面RNN反向传播中T时刻W的梯度公式,我们进一步看一下tanh及其导数的图像,就可以知道他们对应的取值范围:
tanh’的取值在[0,1]之间,如果Ws也在[0,1]之间,这样累乘的结果就可能接近于0;如果Ws是一个很大的值,累乘出来的结果就可能接近于无穷大。这样分别对应了两个我们最不愿意看到的结果,梯度消失和梯度爆炸。拿梯度消失来说,这样就会出现一个问题:
比如我们要训练一个网络,目的是要他预测下面一句话的空格处:
“小明快要高考了,他心仪的学校是北京大学,他曾经去过北大图书馆,觉得…(省略若干字),现在他正在努力,希望能通过自己的努力考上____。
可能对于我们人类来说,能很轻松的说出空格的内容,但是,这么长的句子,在反向传播时,如果发生了梯度消失,网络可能就传播不到句子的最前端,就找不到”北京大学“这个词,这样我们就会比小明还要沮丧了。
那么怎么办,怎么才能解决这类深层RNN中梯度消失/爆炸的问题?于是它来了——LSTM。
LSTM的基本结构
LSTM(Long Short-Term Memory),长短记忆网络,为何要叫这个名字呢?其实这个是针对RNN只能短时记忆的特性来说的,RNN带有短时记忆的缺憾,那我们新推出的网络既然要解决这个问题,所以就叫长一点的短时记忆网络了,LSTM的名字就这么来了。
那么我们来看LSTM的内部结构:
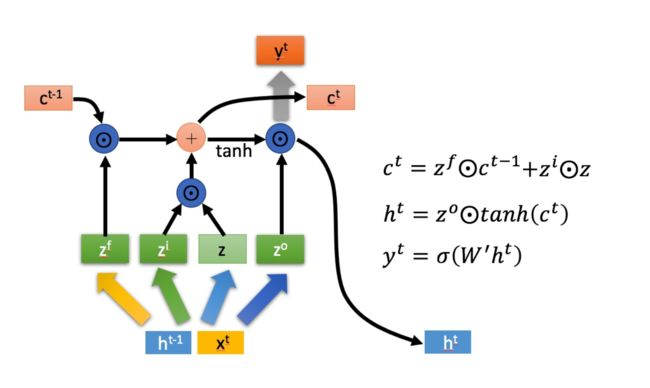
LSTM引入了三个门函数:输入门(Input Gate)、遗忘门 (Forget Gate)和输出门(Output Gate)来控制输入值、 记忆值和输出值,加上我们对输入数据的处理,一共可以得出以下四个状态:

其中, Z(f),Z(i),Z(o)就是我们所说的遗忘门、输入门、输出门,它们是由拼接向量乘以权重矩阵之后,再通过一个sigmoid函数激活映射到(0,1)区间,来作为一种门控状态,z是将由拼接向量乘以权重矩阵之后,通过一个tanh激活函数将结果转换为(-1,1)之间的值,为什么使用tanh?主要是这一块是要将z作为输入数据而不是门控信号。
对于LSTM的内部网络结构,我们一般常见的有两种表现形式,我个人比较喜欢下面这种,看起来更加清晰易理解:
 是Hadamard Product,也就是操作矩阵中对应的元素相乘,因此要求两个相乘矩阵是同型的。
是Hadamard Product,也就是操作矩阵中对应的元素相乘,因此要求两个相乘矩阵是同型的。  则代表进行矩阵加法。
则代表进行矩阵加法。
Hadamard 乘积百度百科定义:
我们看着图来说,LSTM内部其实就是有三个阶段:
-
忘记阶段,对上一个节点传进来的状态进行选择性忘记,即忘记不重要,记住重要的。具体来说是通过计算得到的 Z(f)来作为忘记门控,来控制上一个状态的c(t-1)哪些需要留哪些需要被忘记。
-
选择记忆阶段。这个阶段将本阶段的输入有选择性地进行“记忆”。主要是会对输入x(t)进行选择记忆。哪些重要则着重记录下来,哪些不重要,则少记一些。当前的输入内容由前面计算得到的 z表示。而选择的门控信号则是由Z(i)进行控制。
将上面两步得到的结果相加,即可得到传输给下一个状态的 c(t)。也就是上图中的第一个公式。
-
输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 Z(o)来进行控制的。并且还对上一阶段得到的c(t)进行了放缩(通过一个tanh激活函数进行变化)。与普通RNN类似,输出的y(t)最终通过h(t)变化得到。
这样理解起来就要相对简单一点,我们可以以加法器为中心向外展开,这样更有利于我们的理解和记忆。或者还有一种网络表示方法,更加具象:
对应也有一套更加详细的公式:
其实多种表现形式其核心都是一样的,重点在自己的理解啦。
那么我们之前已经说过了,LSTM的出现是为了解决传统RNN梯度消失或梯度爆炸的问题,那他又是如何解决的呢?
LSTM如何解决传统RNN梯度消失/爆炸的问题?
对于这个问题,解释的角度多种多样,我个人比较倾向的一个角度就是直观从数学的角度来解释:
LSTM解决梯度消失的关键是引入的三个门,特别是遗忘门,它控制了上一时刻网络状态c(t-1)的流入(可以参见上图中c(t)的公式),因为门控中使用sigmoid函数,输出在[0,1]之间,以此实现门控效果。
按照RNN类似的反向传播推导过程,LSTM在反向传播的过程中,对w求偏导会包含:

可以看到被累乘部分最后的取值不是0就是1,如果我们让它为1,这样w的梯度就会变成:
这样就可以解决梯度消失的问题了。但梯度爆炸怎么办,LSTM本身并不能解决梯度爆炸的问题,在LSTM中梯度爆炸只能通过训练中的阈值设定(梯度裁剪)等方法来规避。
还可以有一种更加抽象的理解方式,看这个公式:
f(t)取值是(0,1),当f(t)越接近1,c(t-1)的保留度就越大,网络最先前的特征就更不容易被逐步遗忘,这样长序列信息中后面的信息就更容易和前面的信息产生联系。传统RNN处理长序列信息的不足就可以得到弥补。
LSTM的优化——GRU
LSTM其实已经能基本满足我们对序列信息处理的需求了,但是它还是有一点不足,那就是网络参数比较多,这样训练出来的网络过拟合的风险会更高一点,同时它的训练工作量大成本高,那有没有参数量少一点的网络呢?于是它来了——GRU(Gate Recurrent Unit)。
那为什么GRU就减少参数了呢?根本原因是它将原先LSTM的输入门和遗忘门合并成了一个门,叫做更新门(update gate)。它没有了LSTM中的内部状态和外部状态的划分,而是通过直接在当前网络的状态和上一时刻网络的状态之间添加一个线性的依赖关系,来解决梯度消失和梯度爆炸的问题。
典型的GRU结构图如下:
我们首先来看最重要的更新操作:
来看各个参数:
z就是我们说的更新门,这一步操作是不是遗忘和记忆都做了?因为又是我们熟悉的sigmoid函数,(0,1)区间,实现门控,h(t-1)是要将要被部分遗忘的上一节点传入的状态,h’是要被更新的状态。
再看h’怎么来的:
OK,有一个h(t-1)’,我们看看他又是怎么来的:
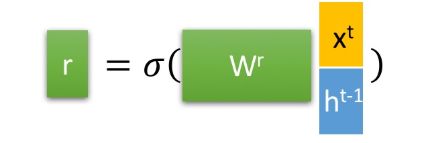
有r:
r叫做重置门(reset gate),就是将上一时刻的状态h(t-1)和当前输入x(t)一起经过了一个sigmoid函数进行了重置。这一系列操作有没有一种LSTM中输入门的感觉??
再对照着上面的结构图看一眼,就会明晰很多。这样门控少了一个,参数量就少了不少,那到底少了多少,我们可以看一下三个网络的对比。
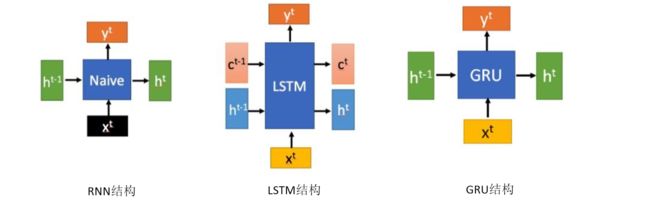
Naive RNN、LSTM、GRU对比
对比上面的网络结构及下面的公式列表:
可以看出LSTM的参数量是Naive RNN的4倍,参数量过多就会存在过拟合的风险,GRU只使用两个门控开关,达到了和LSTM接近的结果。其参数量是Naive RNN的3倍(少了一个门)。理论上来说参数量更大的模型训练出来效果更好的概率要更大一点,但是实际工程应用中GRU由于其参数量少,效果又和LSTM差不多,其应用也更多一点。
参考文章:
人人都能看懂的LSTM
一文搞懂RNN(循环神经网络)基础篇
序列模型简介——RNN, Bidirectional RNN, LSTM, GRU
【串讲总结】RNN、LSTM、GRU、ConvLSTM、ConvGRU、ST-LSTM
LSTM如何解决梯度消失与梯度爆炸
LSTM如何来避免梯度弥散和梯度爆炸?
人人都能看懂的GRU
Navie RNN,LSTM,GRU结构及优缺点