Tensorflow1.x | 学习笔记整理2--简单全连接层实现非线性回归(代价函数、dropout、优化器)

Tensorflow1.x 系列为个人入门Tensorflow1的简要笔记，最近学习的论文涉及到了bilevel program和hypergradient的求解，对应的代码基于Tensorflow1实现，因此根据视频教程学习了解一下Tensorflow。

• 视频课程链接：https://www.bilibili.com/video/BV1wJ411T77b?p=15
• 跟着视频课自己写的代码，使用Colab(https://colab.research.google.com/)
• tips:不同版本的Tensorflow的一些函数用法不一样

---

1 实现一个非线性回归

自己定义一个三层的神经网络，实现一个非线性回归
* 输入层：样本点x–>设置一个神经元
* 中间层：可以自己设置神经元的个数，eg:10个
* 输出层：根据样本点x计算出的y–>一个神经元

%tensorflow_version 1.x
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

# 1.生成数据
x_data = np.linspace(-0.5, 0.5, 200)[:, np.newaxis]  # [-0.5,0.5)范围内等间隔分布的200个点-->转换成200行1列
print(x_data.shape)
noise = np.random.normal(0, 0.02, x_data.shape) # 从均值为0，方差为0.02的高斯分布中随机采200个点
y_data = np.square(x_data) + noise

x = tf.placeholder(tf.float32, [None, 1]) # None表示行不确定
y = tf.placeholder(tf.float32, [None, 1])

# 2.构建神经网络 目的使得根据输入x得到的预测值y接近真实值y_data
"""
输入层：样本点x-->设置一个神经元
中间层：可以自己设置神经元的个数，eg:10个
输出层：根据样本点x计算出的y-->一个神经元
"""
# 2.1 中间层
Weights_L1 = tf.Variable(tf.random.normal([1, 10])) # tf.random.normal():正态分布中随机采样，维度为1*10
biases_L1 = tf.Variable(tf.zeros([1,10])) # 偏置的初始值为0，维度为1*10
Wx_plus_b_L1 = tf.matmul(x, Weights_L1) + biases_L1 # tf.matmul为矩阵乘法
L1 = tf.nn.tanh(Wx_plus_b_L1) # 应用激活函数

# 2.2 输出层
Weights_L2 = tf.Variable(tf.random.normal([10, 1]))
biases_L2 = tf.Variable(tf.zeros([1, 1]))
Wx_plus_b_L2 = tf.matmul(L1, Weights_L2) + biases_L2
prediction = tf.nn.tanh(Wx_plus_b_L2)

# 3.定义损失函数
loss = tf.reduce_mean(tf.square(y - prediction))
optimizer = tf.train.GradientDescentOptimizer(0.1)
train_step = optimizer.minimize(loss)

# 启动默认会话，训练神经网络
with tf.Session() as sess:
  sess.run(tf.global_variables_initializer())

  # 迭代2000次，训练神经网络
  for _ in range(2000):
    sess.run(train_step, feed_dict={x:x_data, y:y_data})
  
  # 获得预测值，训练结束后使用与训练相同的输入样本，观察训练好的模型此时产生的预测值
  prediction_value = sess.run(prediction, feed_dict={x:x_data})

  # 使用图展示结果
  plt.figure()
  plt.scatter(x_data, y_data) # 使用散点图绘制真实样本点
  plt.plot(x_data, prediction_value, 'r-', lw=5)
  plt.show()

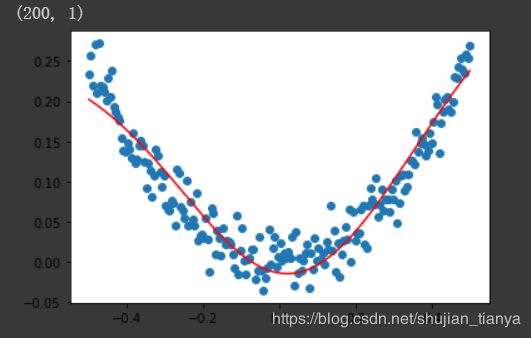
| 得到的输出结果如下：
其中蓝色的点表示随机生成的样本，红色的线表示拟合出的模型曲线

---

2 实现手写数字识别(simple)

这里仅用于展示使用一个简单的网络训练模型去识别mnist数据集
数据集MNIST：

• 训练集样本：mnist.train 60000个样本
• 测试集样本：mnist.test 10000个样本
  其中每张图片尺寸为：28*28(每个像素值为0-1)–>展开成一维向量：784
  训练集:[60000, 784]的tensor
  测试集:[10000, 784]的tensor
  标签：0-9–>转换成one-hot编码:[60000, 10]的矩阵

---

一个简单的神经网络

• 输入层：784个神经元(对应28*28个像素点)
• 输出层：10个神经元(对应0-9类别)

---

Softmax函数：给不同的对分配概率
$softmax(x{)}_i=\frac{exp(x_i)}{{\sum }_{j}exp(x_j)}$

%tensorflow_version 1.x
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

# 1. 加载数据集，联网的情况下会在当前路径自行下载
mnist = input_data.read_data_sets("MNIST_data", one_hot=True) # 加载数据集 加载其onehot编码形式

batch_size = 100 # 定义批次大小，每次选择bacth个样本用于训练
n_batch = mnist.train.num_examples // batch_size # 训练集样本个数//批次大小-->批次个数
x = tf.placeholder(tf.float32, [None, 784]) # 输入样本
y = tf.placeholder(tf.float32, [None, 10])  # 输入样本对应的标签-->ground truth label

# 2.定义简单的神经网路
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
prediction = tf.nn.softmax(tf.matmul(x, W) + b) # 输出的是概率值
loss = tf.reduce_mean(tf.square(y - prediction))
optimizer = tf.train.GradientDescentOptimizer(0.2)
train_step = optimizer.minimize(loss)

# 3.定义变量初始化和准确率
init = tf.global_variables_initializer()    # 所有Variables的初始化
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(prediction, 1))  
'''
求y中最大值的位置，求预测值最大值的位置，并判断二者是否相同
correct_prediction为bool型变量
'''

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))  
'''bool转化成32位浮点型（TRUE：1.， False：0.）-->计算平均值得到准确率'''

# 4.训练网络
with tf.Session() as sess:
  sess.run(init)
  for epoch in range(21):       # 迭代21次
    for batch in range(n_batch):  # 每次分批次训练网络
      batch_xs, batch_ys = mnist.train.next_batch(batch_size) # 获取batch_size个样本，返回图片和标签
      sess.run(train_step, feed_dict={x:batch_xs, y:batch_ys})
    acc = sess.run(accuracy, feed_dict={x:mnist.test.images, y:mnist.test.labels})  # 使用测试集样本计算准确率
    print("Iter:{0}, Test Accuracy:{1}".format(epoch, acc))

| 训练过程如下：
Iter:0, Test Accuracy:0.8296999931335449
Iter:1, Test Accuracy:0.8720999956130981
Iter:2, Test Accuracy:0.881600022315979
Iter:3, Test Accuracy:0.8870999813079834
Iter:4, Test Accuracy:0.8938000202178955
Iter:5, Test Accuracy:0.8964999914169312
Iter:6, Test Accuracy:0.8991000056266785
Iter:7, Test Accuracy:0.9023000001907349
Iter:8, Test Accuracy:0.9031999707221985
Iter:9, Test Accuracy:0.9049000144004822
Iter:10, Test Accuracy:0.906000018119812
Iter:11, Test Accuracy:0.9067999720573425
Iter:12, Test Accuracy:0.9088000059127808
Iter:13, Test Accuracy:0.9092000126838684
Iter:14, Test Accuracy:0.910099983215332
Iter:15, Test Accuracy:0.9108999967575073
Iter:16, Test Accuracy:0.9114000201225281
Iter:17, Test Accuracy:0.911899983882904
Iter:18, Test Accuracy:0.9125999808311462
Iter:19, Test Accuracy:0.9132999777793884
Iter:20, Test Accuracy:0.9140999913215637

3 进一步优化

可以考虑的优化方向：

• 修改batch_size的大小
• 增加隐藏层 设置激活函数和神经元
• 权重和偏差的初始化方法
• 损失函数，eg:交叉熵损失函数
• 优化算法：更改学习率或者其他优化方法
• epoch的确定

"""自己尝试优化的，并没有成功。。。添加中间隐藏层"""
batch_size = 100 # 定义批次大小，每次选择bacth个样本用于训练
n_batch = mnist.train.num_examples // batch_size # 训练集样本个数//批次大小-->批次个数
x = tf.placeholder(tf.float32, [None, 784]) # 输入样本
y = tf.placeholder(tf.float32, [None, 10])  # 输入样本对应的标签-->ground truth label

# 2.定义简单的神经网路-->增加一个隐藏层
with tf.variable_scope("ves_scope", initializer=tf.truncated_normal_initializer(mean=0.0, stddev=2.0, dtype=tf.float32)):
  W1 = tf.get_variable("W1", shape=[784, 50])
  b1 = tf.get_variable("b1", shape=[1, 50])
  W2 = tf.get_variable("W2", shape=[50, 10])
  b2 = tf.get_variable("b2", shape=[1, 10])

L1 = tf.nn.tanh(tf.matmul(x, W1) + b1)
prediction = tf.nn.softmax(tf.matmul(L1, W2) + b2) # 输出的是概率值
loss = tf.reduce_mean(tf.square(y - prediction))
optimizer = tf.train.GradientDescentOptimizer(0.5)
train_step = optimizer.minimize(loss)

4 代价函数的优化

4.1 二次代价函数(quadratic cost)

$C=\frac{1}{2n}\sum ||y(x)-a(x)|{|}^2$
其中：

$C$:代价函数
$x$:输入样本
$y(x)$:样本x对应的实际标签(ground truth label)
$a(x)$:样本x对应的预测结果
$n$:样本总数

若：

$a=\sigma (z)$
$z=\sum w_j\ast x_j+b$

则：

$\frac{\partial C}{\partial W}=\frac{1}{n}\sum (a-y)\ast {\sigma }^{\prime }(z)x$

$\frac{\partial C}{\partial b}=\frac{1}{n}\sum (a-y)\ast {\sigma }^{\prime }(z)$

因此：代价函数对权重和偏差的导数与激活函数的导数在样本点的导数成正比，如果激活函数的导数在某点趋向于0，则导数也趋向于0，不利于梯度下降过程的进行。

4.2 交叉熵代价函数(cross-entropy)

$C=-\frac{1}{n}{\sum }_x[ylna+(1-y)ln(1-a)]$
其中：

$C$:代价函数
$x$:输入样本
$y$:样本对应的实际标签(ground truth label)
$a$:样本对应的预测结果
$n$:样本总数

若：

$a=\sigma (z)=\frac{1}{1+e^{-z}}$
$z=\sum w_j\ast x_j+b$

则：

$\frac{\partial C}{\partial w_j}=-\frac{1}{n}{\sum }_x(\frac{y}{\sigma (z)}-\frac{1-y}{1-\sigma (z)})\ast \frac{\partial \sigma }{\partial w_j}=\frac{1}{n}{\sum }_x{x}_j\ast [\sigma (z)-y]$
$\frac{\partial C}{\partial b}=\frac{1}{n}{\sum }_x[\sigma (z)-y]$

因此：

代价函数对权重和偏差的导数与误差(预测值与真实值)有关，当误差越大时梯度越大，下降越快；反之越慢。
当采用S型激活函数时，相对二次代价函数，交叉熵的效果会好一些。

# 更改损失函数的定义，采用交叉熵损失函数
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y, logits=prediction))

5 训练策略的优化

关于模型的拟合：
(1) 欠拟合(Underfitting)

• 模型不足以拟合训练数据的真实样本分布情况–>存在进一步优化的空间
• 在训练数据和测试数据上表现都不好，模型的bias较大
  (2) 正确拟合
  (3) 过拟合(Overfitting)
• 模型过度拟合训练样本,导致在训练集样本上表现较好而在测试集上表现较差

防止过拟合
(1)增加数据集
(2)采用正则化方法

$C=C_0+\frac{\lambda }{2n}{\sum }_w{w}^2$
$\lambda$用于调整正则项的权重

(3)采用Dropout策略

• 训练过程中选择一部分神经元，测试时使用全部神经元
• 采用dropout之后模型的收敛速度会变慢

"""添加dropout层,设置dropout的概率"""
%tensorflow_version 1.x
import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
# 1. 加载数据集
mnist = input_data.read_data_sets("MNIST_data", one_hot=True) #

batch_size = 100 # 定义批次大小，每次选择bacth个样本用于训练
n_batch = mnist.train.num_examples // batch_size # 训练集样本个数//批次大小-->批次个数
x = tf.placeholder(tf.float32, [None, 784]) # 输入样本
y = tf.placeholder(tf.float32, [None, 10])  # 输入样本对应的标签-->ground truth label
keep_prob = tf.placeholder(tf.float32)

# 2.神经网络，添加dropout层
W1 = tf.Variable(tf.random_normal([784, 2000], stddev=0.1))
b1 = tf.Variable(tf.zeros([2000]) + 0.1)
L1 = tf.nn.tanh(tf.matmul(x, W1) + b1)
L1_drop = tf.nn.dropout(L1, keep_prob)

W2 = tf.Variable(tf.random_normal([2000, 2000], stddev=0.1))
b2 = tf.Variable(tf.zeros([2000]) + 0.1)
L2 = tf.nn.tanh(tf.matmul(L1_drop, W2) + b2)
L2_drop = tf.nn.dropout(L2, keep_prob)

W3 = tf.Variable(tf.random_normal([2000, 1000], stddev=0.1))
b3 = tf.Variable(tf.zeros([1000]) + 0.1)
L3 = tf.nn.tanh(tf.matmul(L2_drop, W3) + b3)
L3_drop = tf.nn.dropout(L3, keep_prob)


W4 = tf.Variable(tf.random_normal([1000, 10], stddev=0.1))
b4 = tf.Variable(tf.zeros([10]) + 0.1)
prediction = tf.nn.softmax(tf.matmul(L3_drop, W4) + b4) # 输出的是概率值
# loss = tf.reduce_mean(tf.square(y - prediction))
loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=y, logits=prediction))
optimizer = tf.train.GradientDescentOptimizer(0.3)
train_step = optimizer.minimize(loss)

# 3.定义变量初始化和准确率
init = tf.global_variables_initializer()    # 所有Variables的初始化
correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(prediction, 1))  
'''
求y中最大值的位置，求预测值最大值的位置，并判断二者是否相同
correct_prediction为bool型变量
'''

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))  
'''bool转化成32位浮点型（TRUE：1.， False：0.）-->计算平均值得到准确率'''

# 4.训练网络
with tf.Session() as sess:
  sess.run(init)
  for epoch in range(31):       # 迭代21次
    for batch in range(n_batch):  # 每次分批次训练网络
      batch_xs, batch_ys = mnist.train.next_batch(batch_size) # 获取batch_size个样本，返回图片和标签
      # 设置dropout的比例，随机丢弃神经元
      sess.run(train_step, feed_dict={x:batch_xs, y:batch_ys, keep_prob:0.7})
    # 计算测试集上的准确率
    test_acc = sess.run(accuracy, feed_dict={x:mnist.test.images, y:mnist.test.labels, keep_prob:1.0})
    # 计算训练集上的准确率
    train_acc = sess.run(accuracy, feed_dict={x:mnist.train.images, y:mnist.train.labels, keep_prob:1.0})  # 使用测试集样本计算准确率
    print("Iter{0}:Test Accuracy:{1}, Train Accuracy:{2}".format(epoch, test_acc, train_acc))

6 优化方法

符号：

$W$:训练模型的参数
$J(W)$:代价函数
${\Delta }_{w}J(W)$:代价函数对参数的导数
$\eta$:学习率

1.经典的梯度下降
2. 随机梯度下降：每次随机选择一个样本–>计算误差–>更新梯度
3. 批量梯度下降：每次从总样本中抽取bath_size个样本
4.带动量的梯度下降 Momentum
基本思想是引入带有历史信息的动量加速梯度下降的过程

$v_t=\alpha v_{t-1}+{\eta }_t{\Delta }_{w}J(W)$
$W=W-v_t$

5.NAG

$v_t=\alpha v_{t-1}+{\eta }_t{\Delta }_{w}J(W-\alpha v_{t-1})$
$W=W-v_t$

6.Adagrad
适用于数据集中样本分布不均匀的情况，即某些类的样本数量较多，而某些类的样本数量可能较少

对于样本较多的类别给予较小的学习率去调整参数，而对于样本较少的类别给予较大的学习率去调整参数

$W_{t+1}=W_t-\frac{\eta }{({\sum }_{t^{\prime }=1}^t(g_{t^{\prime },i}{)}^2+ϵ{)}^{-\frac{1}{2}}}⨀g_t$

其中

$i$:第i类样本
$t$:分类i累计出现的次数
$g_{t,i}={\Delta }_w(W_i)$

7.RMSProp

$E[g^2{]}_t=\alpha E[g^2{]}_{t-1}+(1-\alpha )g_t^2$
$W_{t+1}=W_t-\frac{\eta }{\surd (E[g^2{]}_t)+ϵ}⨀g_t$
其中：
$\alpha$:动量方法中的相同，一般设置为0.9
$E[g^2{]}_t$:表示前t次梯度平方的平均值

8.Adam

$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$
$v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$
$\widehat{m_t}=\frac{m_t}{1-{\beta }_1^t}$
$\widehat{v_t}=\frac{v_t}{1-{\beta }_2^t}$
$W_{t+1}=W_t-\eta \frac{\widehat{m_t}}{(\widehat{v_t}+ϵ{)}^{-\frac{1}{2}}}$