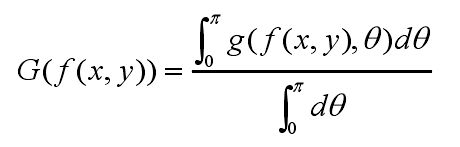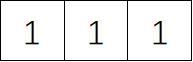基于数学形态学的图像边缘提取方法
Github地址：
最常用的边缘提取方法是基于局部梯度的，参考：低层次的图像特征提取——边缘检测
在基于梯度的经典边缘检测算子中，以Roberts、Prewitt、Sobel、Laplacian算子最为经典和常用。它们都是基于像素的处理方法，具有形式简单、易于实现的优点，但都有定位精度较差、对噪声敏感、准确性不高的缺点，而且被检测出来的边缘通常是不连续和不规则的。
Huechel最早提出亚像素边缘检测技术，现已发展为插值、矩法和最小二乘法等多种检测方法。插值法计算时间相对较短，但定位精度低，抗噪声能力差；矩法和最小二乘法定位精度高，抗噪声能力强，但计算复杂度高，且最小二乘法需要有一定先验知识，很难适应在线检测的需要。
将边缘作为配准特征进行图像配准时，边缘的准确性直接决定了配准结果的正确性和精确性。前述的经典边缘提取算子，都具有对噪声敏感和边缘定位精度低的问题，采用经典边缘提取算子很难满足前述对边缘的准确性、精确性和单边响应的要求。由于数学形态学的方法有较好的并行计算能力和适应性，因此可以用来代替经典边缘提取算子。
数学形态学
数学形态学(Mathematical Morphology)，是基于积分几何和几何概率理论建立的关于图像形状和尺寸的研究方法，其实质是一种非线性滤波方法。数学形态学的方法应用于视觉图象的处理就是用具有一定形状、大小的结构元素去探测、度量和提取图象中的对应形状，以达到对图像进行处理、分析、识别的目的。数学形态学处理能简化图像数据，在保持图像基本形状特性的同时去除不相干的结构。
目前，数学形态学已经广泛用于噪声抑制、特征提取、形状识别、纹理分析、图像恢复与重建等图像处理问题中。在图像处理中，主要使用的是二值形态学和灰度形态学。形态学方法对图像数据的基本操作都是膨胀(Dilation)、腐蚀(Erosion)以及建立在这两种运算基础之上的开(Open)运算和闭(Close)运算，膨胀可以填充孔洞，而腐蚀则可以去除孤点和尖峰。
二值形态学运算
A被B膨胀的结果为~B被所有x平移后与A至少有一个非零的公共元素。
A被B腐蚀的结果为所有使B被x平移后包含于A的点x的集合。
A被B开运算就是A被B腐蚀后的结果再被B膨胀。
A被B闭运算就是A被B膨胀后的结果再被B腐蚀。
基于方向的灰度形态学边缘提取
形态学轮廓提取
形态学提取图像轮廓有3种方法，即（符号⊕表示膨胀运算，Θ表示腐蚀运算）：
1）f⊕b − f
2）f − fΘb
3）f⊕b − fΘb
三种方案的边缘提取结果对比
| 原图 |
|
| 方案1 |
|
| 方案2 |
|
| 方案3 |
|
方法1）在提取高灰度值、小间距的轮廓时，容易产生轮廓错位和合并，导致检测不准确。方法2）则容易引起间距小的低灰度轮廓的错位和合并。方法3）又称作形态学梯度，对噪声敏感且提取的轮廓较粗，而且要进行膨胀和腐蚀操作各一次，因而计算复杂度大。根据用配准的边缘准则，在用轮廓进行配准定位时，若轮廓越细腻和完整，则配准结果越精确。由于低灰度轮廓的特征不明显，因此，为了保证高灰度值轮廓点的准确提取，方法2）最适合用于轮廓提取。
基于方向的灰度形态学轮廓提取
对图像构造如下边缘模型：
（4）
其中，b为背景灰度，a为轮廓幅值，θ为轮廓的方向，则轮廓可通过对各方向提取到的轮廓进行合成。令g( f(x，y)，θ)表示在方向θ提取的轮廓，则最终的轮廓合成可表示成：
（5）
考虑到从区间[0，
]，和区间[，2]的对称性，上式改写成：
(6)
显然，如果将此式直接用于轮廓提取的计算，首先要确定角度分辨率，然后提取各方向上的轮廓，再将所有方向的轮廓进行合成。在对各方向轮廓提取时，必须根据角度分辨率对图像进行插值运算，这将会带来极大的计算复杂度。
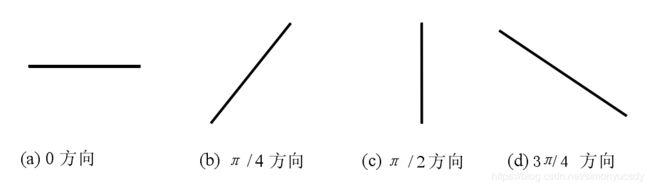
基于此，考虑使用一系列带有方向性的一维形态学算子对图像进行多角度的轮廓提取，然后再对各方向上的图像轮廓进行综合即可得到整个图像的轮廓，为了简单起见，避免对图像进行复杂的插值运算，选择规则的角度方向：0、/4、/2、3/4。
对于图像只需要进行坐标平移的配准的情形，只考虑提取图像在横向和纵向上的轮廓即可满足配准条件，即只需要提取0方向和/2方向的轮廓。为了保证检测的边缘位置的精确，在提取横向轮廓时，应尽量减少纵向轮廓点可能带来的影响；反之，在提取纵向轮廓时，尽量减少横向轮廓点带来的影响；采用的算子如图所示：
0方向算子
pi/2方向算子
opencv的基于方向的形态学边缘检测实现：
预测的双阈值边缘分割
在边缘提取出来后，考虑到算法误差带来噪声和漏判。因此，要进一步判断是否是真的边缘点并且将图像进行二值化，双阈值边缘分割法是最常用的方法。
首先，选择一个较大的阈值T，然后再取一小阈值T'=0.8T。
然后，逐像素进行双阈值处理，对每一个像素考虑三种情况：如果该像素点灰度值大于高阈值，那么它一定是边缘；如果该像素点灰度值低于小阈值，那么它一定不是边缘；如果该像素点灰度值介于两者之间，则考虑其8邻域像素点的灰度值有没有大于高阈值的，如果有则将其视为轮廓点，否则视为非轮廓点。