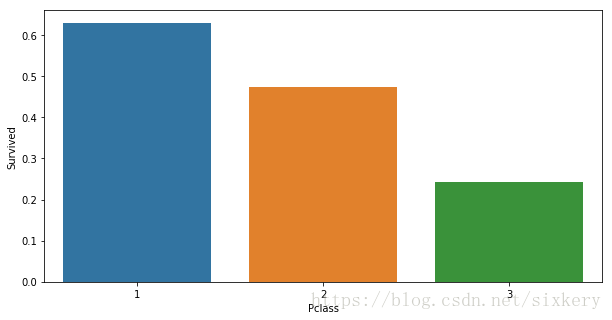python 分析泰坦尼克号生还率
泰坦尼克号数据集,是kaggle(Titanic: Machine Learning from Disaster)上入门机器学习(ML)的一个好的可选数据集,当然,也是不错的练习数据分析的数据集。对 python ,在数据分析方面,作为一柄利器,涵盖了「数据获取→数据处理→数据分析→数据可视化」这个流程中每个环节,这个项目作为新生练习最好不过了。
探索的问题
主要探寻坦尼克号上的生还率和各因素(客舱等级、年龄、性别、上船港口等)的关系。
获取数据
我把原始数据 titanic-data.csv 放在和 notebook 文件同一目录下,然后通过read_csv 来载入文件,当然在开始载入数据前,我必须按照需求将需要用到的 Python 包导入进来。
# 用于数据分析
import pandas as pd
import numpy as np
# 用于绘图
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# 读取前五行数据
data_t = pd.read_csv('titanic-data.csv')
data_t.head()
| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th... | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
# 数据集信息,包含数据集大小,列名,类型
data_t.info()
data_t.columns.values
RangeIndex: 891 entries, 0 to 890
Data columns (total 12 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 714 non-null float64
SibSp 891 non-null int64
Parch 891 non-null int64
Ticket 891 non-null object
Fare 891 non-null float64
Cabin 204 non-null object
Embarked 889 non-null object
dtypes: float64(2), int64(5), object(5)
memory usage: 83.6+ KB
array(['PassengerId', 'Survived', 'Pclass', 'Name', 'Sex', 'Age', 'SibSp',
'Parch', 'Ticket', 'Fare', 'Cabin', 'Embarked'], dtype=object)
数据观察
-
载入 titanic-data.csv 到一个 DataFrame ,然后用 head() 函数打印出前5行数据(p.s 用 tail() 函数可以打印出后5行)。
-
通过对数据的初步观测,这个数据样本一共有 891 行 * 12 列数据,字段包含:
‘PassengerId(乘客id)’, ‘Survived(是否活下来)’, ‘Pclass(船舱等级)’, ‘Name(姓名)’, ‘Sex(性别)’, ‘Age(年龄)’, ‘SibSp(兄弟姐妹同行数量)’,‘Parch(父母配偶同行数量)’, ‘Ticket(票)’, ‘Fare(费)’, ‘Cabin(船舱)’, ‘Embarked(上船站)’ -
其中, 定类变量 包括 Survived,Sex,Embarked, 定序变量 包括 Pclass, 数字变量 包括 PassengerId,Age,SibSp,Parch,Fare
-
通过观测发现,Age、Cabin、Embarked 包含了有空值
# 字段分析
def y(x):
return data_t[x].unique()
print('='*20 + 'Survived字段内容' + '='*20)
print(y('Survived'))
print('='*20 + 'Sex字段内容' + '='*20)
print(y('Sex'))
print('='*20 + 'Pclass字段内容' + '='*20)
print(y('Pclass'))
print('='*20 + 'Embarked字段内容' + '='*20)
print(y('Embarked'))
====================Survived字段内容====================
[0 1]
====================Sex字段内容====================
['male' 'female']
====================Pclass字段内容====================
[3 1 2]
====================Embarked字段内容====================
['S' 'C' 'Q' nan]
变量的值
- Survived 的值:0(死亡),1(存活)
- Sex 的值:male(男性),female(女性)
- Embarked的值包含 ‘S’ ‘C’ ‘Q’
# 显示重复的数据数量
data_t.duplicated().value_counts()
False 891
dtype: int64
重复数据
数据集一共有 891 行数据,不重复。
# 显示有空值的列
print(data_t['Age'].isnull().value_counts())
print('-'*50)
print(data_t['Cabin'].isnull().value_counts())
print('-'*50)
print(data_t['Embarked'].isnull().value_counts())
print('-'*50)
False 714
True 177
Name: Age, dtype: int64
--------------------------------------------------
True 687
False 204
Name: Cabin, dtype: int64
--------------------------------------------------
False 889
True 2
Name: Embarked, dtype: int64
--------------------------------------------------
空值情况
- Age 一共有 714 行空数据
- Cabin(船舱)一共有 204 行空数据
- Embarked(上船站)一共有 2 行空数据。
# 描述性分析
data_t.describe()
| PassengerId | Survived | Pclass | Age | SibSp | Parch | Fare | |
|---|---|---|---|---|---|---|---|
| count | 891.000000 | 891.000000 | 891.000000 | 714.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 446.000000 | 0.383838 | 2.308642 | 29.699118 | 0.523008 | 0.381594 | 32.204208 |
| std | 257.353842 | 0.486592 | 0.836071 | 14.526497 | 1.102743 | 0.806057 | 49.693429 |
| min | 1.000000 | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 223.500000 | 0.000000 | 2.000000 | 20.125000 | 0.000000 | 0.000000 | 7.910400 |
| 50% | 446.000000 | 0.000000 | 3.000000 | 28.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 668.500000 | 1.000000 | 3.000000 | 38.000000 | 1.000000 | 0.000000 | 31.000000 |
| max | 891.000000 | 1.000000 | 3.000000 | 80.000000 | 8.000000 | 6.000000 | 512.329200 |
描述性统计
- 在这次旅行的 891 名乘客中,有 38% 的人活了下来,幸运儿。
- 所有旅客中,年龄最小的只有 0.4 岁,最大的有 80 岁,平均年龄在 28 岁左右。
- 平均每个乘客有 0.52 个兄弟姐妹陪同,有 0.38 个父母配偶陪同。
- 有些乘客居然有 8 名同行的人。
- 旅客为这趟旅行平均花费 32 美元,最高花费 512 美元(贵族吧)
数据清洗(cleanse the data)
题外话
据说数据清洗这一块在实际业务中大概占有 80% 的时间,可真是苦逼。
缺失值处理中,我们一般会删除缺失值。pandas模块中,提供了将包含NaN值的行删除的方法dropna(),但其实处理缺失值最好的思路是用最接近的数据替换
首先,清洗数据就是处理空值,让这些空值参与到之后的数据分析中去。其次,我将删除那些对于数据分析本身并没有相关性的数据列,比如Cabin(因为一个船舱号对于是否能够逃生确实没有任何影响)。最后,我会观察数据集,看看是否可以创造出一些新的特性,让我们的分析能够更直观快捷。
# 处理空值
data_t['Age'] = data_t['Age'].fillna(data_t['Age'].mean()).astype(np.int64)
data_t['Embarked'] = data_t['Embarked'].fillna({"Embarked":"S"},inplace=True)
# 删除无关的列
data_t = data_t.drop(['Ticket','Cabin'],axis='columns')
data_t.info()
RangeIndex: 891 entries, 0 to 890
Data columns (total 10 columns):
PassengerId 891 non-null int64
Survived 891 non-null int64
Pclass 891 non-null int64
Name 891 non-null object
Sex 891 non-null object
Age 891 non-null int64
SibSp 891 non-null int64
Parch 891 non-null int64
Fare 891 non-null float64
Embarked 0 non-null object
dtypes: float64(1), int64(6), object(3)
memory usage: 69.7+ KB
处理空值和多余的值
上面用年龄的平均数来代替空值,因为 ‘S’ 出现的频数最多,咖位最高,所以用 ‘S’ 代替空值。
我删除掉了 ‘Ticket’,‘Cabin’ 两列数据,实际上这两列数据对于我们分析数据并没有太多用处。
数据可视化分析
数据透视表是 Excel 中最常用的数据汇总分析工具,它可以根据一个或多个制定的维度对数据进行聚合,探索数据内深层次的信息。
在 pandas 中,同样提供了pandas.pivot_table 函数来实现这些功能。在接下来的分析中,我们会多次用到这个函数,所以先来熟悉下下这个函数:
pandas.pivot_table 函数中包含四个主要的变量,以及一些可选择使用的参数。四个主要的变量分别是数据源 data,行索引 index,列 columns,和数值 values。可选择使用的参数包括数值的汇总方式,NaN值的处理方式,以及是否显示汇总行数据等。
基本情况分析
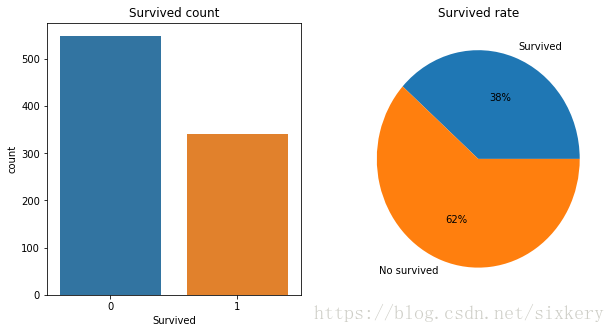
我们先来看下基本情况:891人当中,生还比率与未生还比率是多少?
total_survived = data_t['Survived'].sum()
total_no_survived = 891 - total_survived
plt.figure(figsize = (10,5)) # 创建画布
plt.subplot(121) # 添加第一个子图
sns.countplot(x='Survived',data=data_t)
plt.title('Survived count')
plt.subplot(122) # 添加第二个子图
plt.pie([total_survived,total_no_survived],labels=['Survived','No survived'],autopct='%1.0f%%')
plt.title('Survived rate')
plt.show()
结论:这891名乘客中,生还和未生还的比率分别为 38% 和 62%。
分别探索下 Pclass、Sex、Age 和 Embarked 等与“生还率”的关系.
舱位(Pclass)与生还率关系
把 pivot_table 派上场。
# 不同船舱人数分布
data_t.pivot_table(values='Name',index='Pclass',aggfunc='count')
| Name | |
|---|---|
| Pclass | |
| 1 | 216 |
| 2 | 184 |
| 3 | 491 |
传几个参数就出来了,是不是很方便。
如果不使用 pivot_table 函数,我们一般用 group_by 来分组聚合。
data_t[['Pclass','Name']].groupby(['Pclass']).count()
| Name | |
|---|---|
| Pclass | |
| 1 | 216 |
| 2 | 184 |
| 3 | 491 |
比较来说,pivot_table 函数可读性更高。
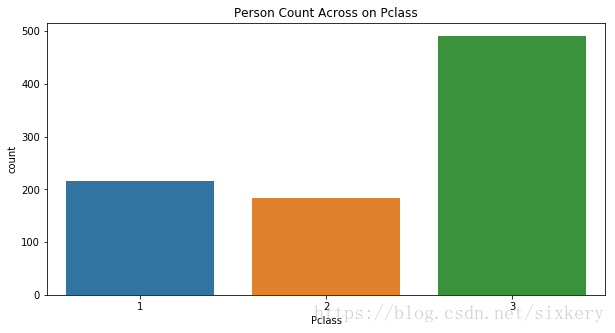
可视化操作
plt.figure(figsize = (10,5)) # 创建画布
sns.countplot(x='Pclass',data=data_t)
plt.title('Person Count Across on Pclass')
plt.show()
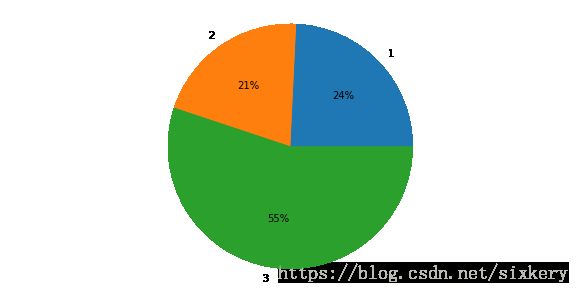
还可以用饼图。
plt.figure(figsize = (10,5)) # 创建画布
plt.pie(data_t[['Pclass','Name']].groupby(['Pclass']).count(),labels=['1','2','3'],autopct='%1.0f%%')
plt.axis("equal") #绘制标准的圆形图
plt.show()
好了,这是不同舱位的人数分布情况,我们需要求出的是舱位与生还率的关系。
舱位与生还率的关系
data_t.pivot_table(values='Survived',index='Pclass',aggfunc=np.mean)
| Survived | |
|---|---|
| Pclass | |
| 1 | 0.629630 |
| 2 | 0.472826 |
| 3 | 0.242363 |
可视化操作
plt.figure(figsize= (10 ,5))
sns.barplot(data=data_t,x="Pclass",y="Survived",ci=None) # ci表示置信区间
plt.show()
结论:头等舱的生还概率最大,其次是二等舱,三等舱的概率最小。
性别(Sex)与生还率关系
# 不同性别生还率
data_t.pivot_table(values='Survived',index='Sex',aggfunc=np.mean)
| Survived | |
|---|---|
| Sex | |
| female | 0.742038 |
| male | 0.188908 |
可视化操作
plt.figure(figsize=(10,5))
sns.barplot(data=data_t,x='Sex',y='Survived',ci=None)
plt.show()
结论:女性幸存概率远远大于男性。
综合考虑性别(Sex),舱位(Pclass)与生还率关系
#首先计算不同舱位不同性别的人的生还概率
data_t.pivot_table(values='Survived',index=['Pclass','Sex'],aggfunc=np.mean)
| Survived | ||
|---|---|---|
| Pclass | Sex | |
| 1 | female | 0.968085 |
| male | 0.368852 | |
| 2 | female | 0.921053 |
| male | 0.157407 | |
| 3 | female | 0.500000 |
| male | 0.135447 |
可视化操作
plt.figure(figsize=(10,5))
sns.pointplot(data=data_t,x='Pclass',y='Survived',hue='Sex',ci=None)
plt.show()
结论
- 在各个船舱中,女性的生还率都大于男性。
- 一二等船舱中女性生还率接近,且远大于三等舱。
- 一等舱的男性生还率大于二三等舱,二三等舱男性生还率接近。
年龄(Age)与生还率关系
与上面的舱位、性别这些分类变量不同,年龄是一个连续的数值变量,一般处理这样的数据类型,我们采用将连续性的变量离散化的方法。
所谓离散化,指的是将某个变量的所在区间分割为几个小区间,落在同一个区间的观测值用同一个符号表示,简单理解就是将属于统一范围类的观测值分为一组。然后分组观察。
pandas中提供了cut函数,对变量进行离散化分割。
data_t['AgeGroup'] = pd.cut(data_t['Age'],5) # 将年龄的列数值划分为五等份
data_t.AgeGroup.value_counts(sort=False)
(-0.08, 16.0] 100
(16.0, 32.0] 525
(32.0, 48.0] 186
(48.0, 64.0] 69
(64.0, 80.0] 11
Name: AgeGroup, dtype: int64
各个年龄段的生还率
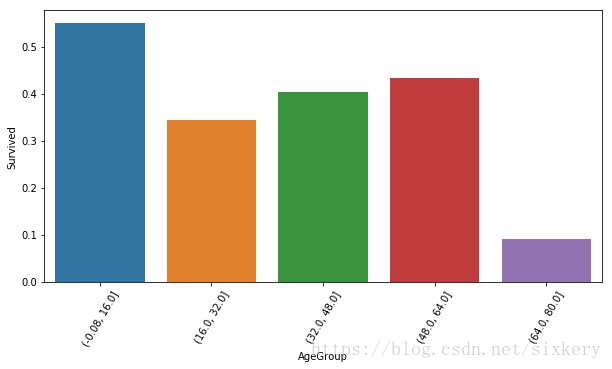
data_t.pivot_table(values='Survived',index='AgeGroup',aggfunc=np.mean)
| Survived | |
|---|---|
| AgeGroup | |
| (-0.08, 16.0] | 0.550000 |
| (16.0, 32.0] | 0.344762 |
| (32.0, 48.0] | 0.403226 |
| (48.0, 64.0] | 0.434783 |
| (64.0, 80.0] | 0.090909 |
可视化操作
plt.figure(figsize=(10,5))
sns.barplot(data=data_t,x='AgeGroup',y='Survived',ci=None)
plt.xticks(rotation=60) # 设置标签刻度角度
plt.show()
结论:儿童少年组的生还率更高。
多因素分析
以上是单独看年龄/性别/舱位和生还率的关系,下面我们综合多个因素来看生还率。
年龄(Age),性别(Sex)与生还率关系
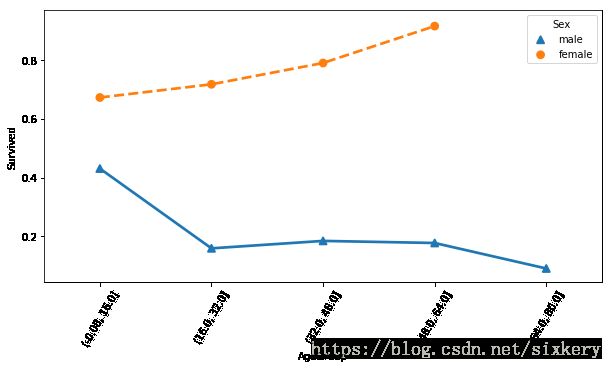
data_t.pivot_table(values='Survived',index='AgeGroup',columns='Sex',aggfunc=np.mean)
| Sex | female | male |
|---|---|---|
| AgeGroup | ||
| (-0.08, 16.0] | 0.673469 | 0.431373 |
| (16.0, 32.0] | 0.718391 | 0.159544 |
| (32.0, 48.0] | 0.791045 | 0.184874 |
| (48.0, 64.0] | 0.916667 | 0.177778 |
| (64.0, 80.0] | NaN | 0.090909 |
可视化操作
plt.figure(figsize= (10 ,5))
sns.pointplot(data=data_t,x="AgeGroup",y="Survived",hue="Sex",ci=None,
markers=["^", "o"], linestyles=["-", "--"])
plt.xticks(rotation=60)
plt.show()
结论:儿童少年,女性的生还率更高。男性生还的基本上都是儿童少年。
年龄(Age),性别(Sex),舱位(Pclass)与生还率关系
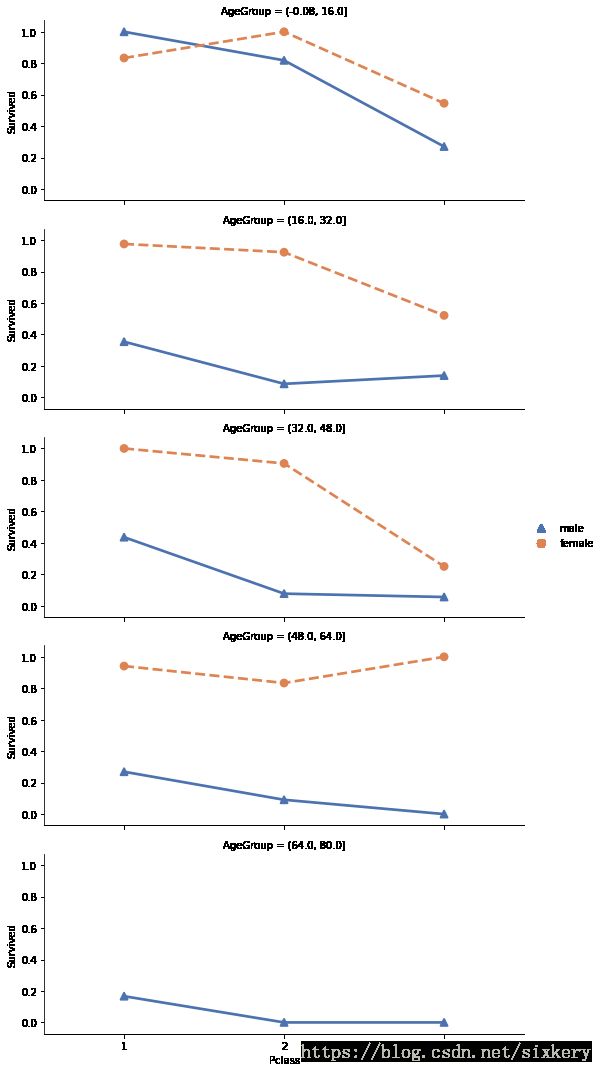
data_t.pivot_table(values="Survived",index="AgeGroup",columns=["Sex","Pclass"],aggfunc=np.mean)
| Sex | female | male | ||||
|---|---|---|---|---|---|---|
| Pclass | 1 | 2 | 3 | 1 | 2 | 3 |
| AgeGroup | ||||||
| (-0.08, 16.0] | 0.833333 | 1.000000 | 0.545455 | 1.000000 | 0.818182 | 0.270270 |
| (16.0, 32.0] | 0.975610 | 0.923077 | 0.521277 | 0.354167 | 0.086207 | 0.138776 |
| (32.0, 48.0] | 1.000000 | 0.904762 | 0.250000 | 0.435897 | 0.076923 | 0.055556 |
| (48.0, 64.0] | 0.941176 | 0.833333 | 1.000000 | 0.269231 | 0.090909 | 0.000000 |
| (64.0, 80.0] | NaN | NaN | NaN | 0.166667 | 0.000000 | 0.000000 |
可视化操作
sns.FacetGrid(data=data_t,row="AgeGroup",aspect=2.5)\
.map(sns.pointplot,"Pclass","Survived","Sex",hue_order=["male","female"],ci=None,palette="deep",
markers=["^", "o"], linestyles=["-", "--"]).add_legend()
plt.show()
总结
本次分析主要探寻泰坦尼克号上的生还率和各因素(客舱等级、年龄、性别、上船港口等)的关系。
样本数量为 891,海难发生后,生还者还剩 342 人,生还率为 38%。
泰坦尼克号上有一\二\三等舱三种船舱类型,其中头等舱的生还概率最大,其次是二等舱,三等舱的概率最小。
891人中,男性共577人,女性314人,女性生还率远远大于男性。可见女性比男性在这次事故中更容易生还,表明“女士优先”的原则在本次事故中得到了发扬。
样本的 891 人中,最小年龄为 0.42 ,最大年龄 80。按照[(0.34, 16.336] < (16.336, 32.252] < (32.252, 48.168] < (48.168, 64.084] < (64.084, 80.0]]划分原则,划分为5组,儿童少年组的生还率最高,年龄越大,生还率越低。“尊老爱幼”的原则在本次事故中没有很好体现。
样本的 891 人中,从 C 上船的生还率最高, Q上船的 次之, S上船生还率 最低。
最后需要说明的是,此次数据分析的数据集是从总体中抽样而来的,如果抽样无偏,样本是从总体随机选取,根据中心极限定理,分析结果具有代表性,如果不是随机选出,那么分析结果就不可靠了。