风控模型评估方法以及大数据风控模型概念

更新一下有效性指标中的区分能力指标：

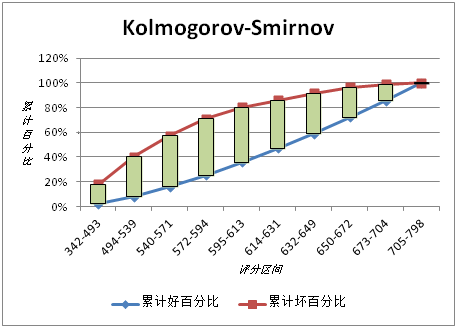
KS(Kolmogorov-Smirnov)：KS用于模型风险区分能力进行评估，指标衡量的是好坏样本累计分部之间的差值。好坏样本累计差异越大，KS指标越大，那么模型的风险区分能力越强。

KS的计算步骤如下：

1. 计算每个评分区间的好坏账户数。

2. 计算每个评分区间的累计好账户数占总好账户数比率(good%)和累计坏账户数占总坏账户数比率(bad%)。

3. 计算每个评分区间累计坏账户占比与累计好账户占比差的绝对值（累计good%-累计bad%），然后对这些绝对值取最大值即得此评分卡的K-S值。

·GINI系数:也是用于模型风险区分能力进行评估。GINI统计值衡量坏账户数在好账户数上的的累积分布与随机分布曲线之间的面积，好账户与坏账户分布之间的差异越大，GINI指标越高，表明模型的风险区分能力越强。

GINI系数的计算步骤如下：

1. 计算每个评分区间的好坏账户数。

2. 计算每个评分区间的累计好账户数占总好账户数比率（累计good%）和累计坏账户数占总坏账户数比率(累计bad%)。

3. 按照累计好账户占比和累计坏账户占比得出下图所示曲线ADC。

4. 计算出图中阴影部分面积，阴影面积占直角三角形ABC面积的百分比，即为GINI系数。

以下是原文

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

楼主范围太广。不同的行业有不同的风控目标，不同的风控过程和程度，也有不同的风控结果。其次同一行业风险也分多种风险，对不同的风险（信用风险，操作风险，市场风险）也有不同的应对办法以及模型建设。

只讲一讲中国金融行业中的银行的信用风控与大数据的渊源。

1，风控意义与大数据建模分析优点:中国的金融行业必定在金融全球化的洗礼下一步步找到更大市场，相比中国制造业有成长更快的趋势。而此刻，风控就显得尤为重要。都知道收益越大风险越大，当然而我们更想的如果是在中间找到一个平衡点让收益大的情况下拥有尽可能小的风险。而大数据建模就可以尽可能实现这点:提高审批效率，降低人工成本，减少因非客观判断原因造成的失误的风险。

2,大数据建模目标。第一点目标做信贷工厂的量化建设:清洗银行历史数据用于数据建模形成评分卡，再与规则结合对贷款生命周期三个阶段（申请贷后催收）的好坏客户提供决策建议的预测框架（自动通过，人工审核，审慎审核，还是建议拒绝）。第二点目标内评合规:背景是巴塞尔协议:衡量银行的资本充足率和资本准备是符合巴塞尔协议的规定，如果不符合应该采取什么样的措施。

3，关于建模:前:建模的变量以及数据都是通过层层原始分析，挖掘分析，变量分组，变量降维，过度拟合VIF检测，以及业务逻辑选择出来的。中:而模型的建设本来有方差分析，相关性分析，逻辑回归，决策树，神经网络分析这几种。但是由于Y变量都一般为非线性所以基本都用LOGISTIC逻辑回归。后:模型建好后还需要用PSI检验模型客群的稳定性，用KS或者GINI函数检验模型的区分能力。（公式我就不给啦~感兴趣的孩子肯定有自己学习的方式）如果不太理想就再改进，这是一个做循环的闭环式过程直到选到最佳的。（PS:建模工具:SAS，由于可以处理相当庞大的数据且在美国极其权威的认证而著称的。别的我就不评价了嘿）

4,好的信用风控的评估效果一主要从准确性，稳定性，可解释性三个方面来评估模型。其中准确性指标包括感受性曲线下面积(ROC_AUC)和区分度指标(Kolmogorov-Smirnov，KS)，稳定性指标主要参考群体稳定指数(Population Shift Index，PSI)。可解释性可通过指标重要度来进行评估，其中指标重要度用于衡量各个解释变量对算法预测结果影响的程度。注意:一定要将大数据建模与业务逻辑紧密联系!

分割线----------------------------------------------------------当然，个人觉得知道模型背后的理论也是非常有必要的。让我们顺着逻辑回归来讲。一首先是假设检验中假设建立。什么是假设检验呢，假设检验背后的原理是什么呢，我们模型中具体的假设是什么呢。

假设检验分为原假设H和备择假设H0，我们后面会推翻H来证明我们的H0是正确的。

假设检验的原理也就是我们要推翻的这个H的理由是:小概率事件不可能发生。（在此我举一个经典的例子）

在模型中我们的假设便是我们逻辑回归的因变量和自变量之间没有线性关系。

也就是这里面的beta们都是0。

二，never say yes.在原假设正确的前提下，确定检验统计数并计算出统计数的估计值（即构造统计量并计算统计量的估计值)

一般我们会把统计量构造成符合正态分布、卡方分布、F分布的情况，由构造的统计量不同可分为u检验、卡方检验、F检验等。

这里我们以卡方分布统计量为例子：

在各种假设情形下，实际频数与理论频数偏离的总和即为卡方值，它近似服从卡方为V的卡方分布，因此可以用卡方分布的理论来进行假设检验。

三、计算P值，或确定临界值，并比较临界值与统计数值的大小，根据”小概率事件在一次实验中几乎是不可能发生的原理“得出结论统计结果分析

显著性水平：这里的显著是一个统计学的概念，是指原假设发生是一个小概率事件，统计学上用来确定或否定原假设为小概率事件的概率标准叫做显著性水平。原假设发生的概率如果小于或等于5%，一般认为认为是小概率事件，这也是统计学上达到了”显著“，这时的显著性水平为5%。

拒绝域：当由样本计算的统计量落入该区域内则拒绝原假设，接受备择假设，拒绝域的边界称为临界值。当原假设正确时，它被拒绝的概率不得超过给定的显著性水平a（阿尔法），阿尔法通常取值为0.05,0.01，因此落在拒绝域内是一个小概率事件。

还是以卡方检验为例

以下是卡方分布的密度函数，X轴是卡方值，Y轴是发生的P概率。

换句简单易懂的话就是，我们计算实际频数与理论频数的偏离程度即卡方值非常大的情况下概率是非常小的是不会发生的，当X2卡方值远远大于3.84，相应的我们X轴远方对应的就是越来越小的P概率。那么也就是说我们的假设是不成立的，也就是说因变量和自变量之间他们是相关的。并且在原假设情况下卡方值越大也就代表越不可能不相关，也就是越可能相关。

当然在确定检验我们单个系数的时候会用来卡方检验，整个模型的检验的时候就会用到我们F检验，T检验，他们都和我们的卡方有一定的联系。

Logistic制作评分卡模型的衡量标准是K-S值的大小，依据数据质量和建模能力在0-0.5之间，一般在0.3以上才可用，好的模型可以达到0.35。

芝麻分模型的K-S值在0.32左右。