计算图（computational graph）角度看BP（back propagation）算法

从计算图（computational graph）角度看BP（back propagation）算法，这也是目前各大深度学习框架中用到的，Tensorflow, Theano, CNTK等。参考【1】

一、通用形式

1. 什么是计算图结构
从下图中我们可以清楚地看到
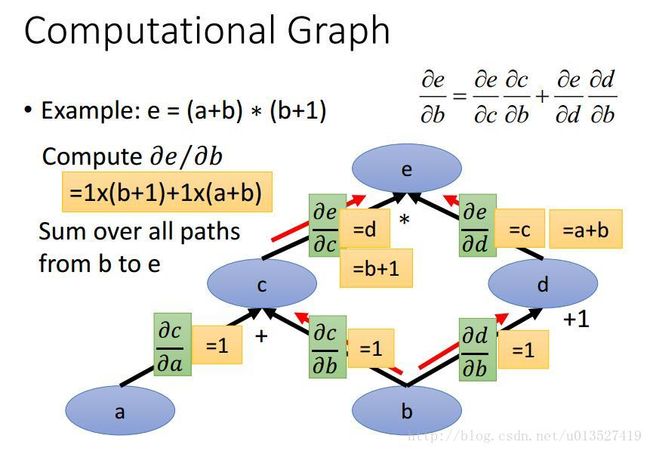
（1）可以将计算图看作是一种用来描述function的语言，图中的节点node代表function的输入（可以是常数、向量、张量等），图中的边代表这个function操作。
（2）看到一个计算图的例子，我们就可以很容易地写出其对应的function。

2.用计算图和链式法则来算偏导数

从下图中中的计算图我们可以得到它对应的function：e = (a+b) ∗ (b+1)，若我们要求e对b的偏导数，可经过以下步骤求得：

（1）图中绿色部分计算每一条edge上的偏导数，easy。
（2）从e到参数b有两条路径，把这两条路径上计算出的偏导数相乘，最后相加即为所求目标。（图中红色箭头）

举个例子：
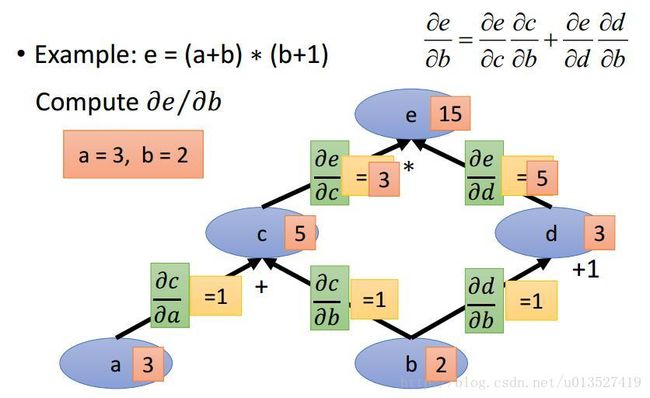
若已知a = 3, b = 2，求e对b的偏导数：
（1）首先，前向计算很容易得到c，d，e的值（下图中橘红色的部分，很容易）
（2）算出每条路径上的偏导数值（下图中黄色部分，很容易）
（3）从节点b开始找到从自身节点到目标节点e有两条路径，每条路径上偏导数相乘后的结果为1*3和1*5，最后相加得到结果8。

3.如果要求同时求一个参数对多个参数的偏导数呢？
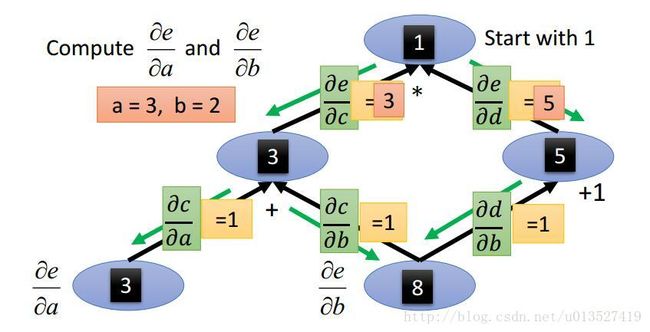
例如下图中要求同时求e对a，b的偏导数：
法一：按照2中的步骤分别求出来即可，这样子的话如果参数很多，分别求就很没效率。（称为 forward mode）
法二：可以反方向来求，如下图中绿色箭头，这样遍历一次图就可以同时求出来，更快。（称为 reverse mode）
此法适用于有一个root的结构，例如在神经网络中，我们用到就是reverse mode，因为在NN中，我们要求的就是最终的loss function的偏微分，这个function的输出就只有一个，要算这个loss function对所有参数的偏微分，反向更有效率。

4.如果计算图中有Parameter sharing（即同一个参数出现在多个不同的node上）的状况呢？
Parameter sharing也是NN中经常发生的事，例如CNN,RNN中都有。
步骤：
（1）计算每一条边上的偏微分，如下图中绿色箭头，注意计算中将相同的参数看作不同的对待，如将x看作带不同下标的x==
（2）将y到三个x的三条路径的偏微分之乘相加即可。

即遇到Parameter sharing的情况时，先将同一个参数相当做不同的参数来看，算完之后再相加。

二、全连接神经网络中的计算图

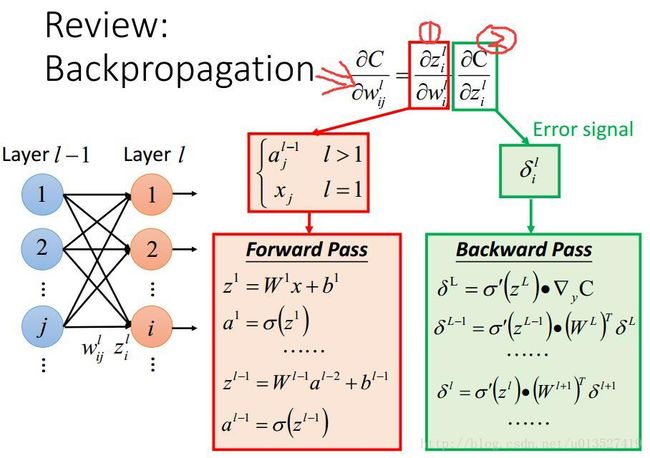
1.先复习一下bp算法
详见：反向传播（back propagation）算法学习笔记
简而言之，如下，
第一个红色框中的部分第l层的第i个神经元对与其相连的j个权重的偏导数分别为l-1层中每一个权重参数w连接的那个神经元的输出，这个通过一个前向传播就可以很容易求出所有的偏导数值。
第二个绿色框中的部分loss function对第l层的神经元的输入z的偏导可以通过将误差后向递归传播得到。

2.用计算图来做bp
首先将神经网络画成计算图的形式，w，b都是参数，都是节点。然后再按照刚才讲过的步骤依次求每一个箭头上的偏导数，最后将每条路径上的偏导数相乘最后想加即可。用 reverse mode做

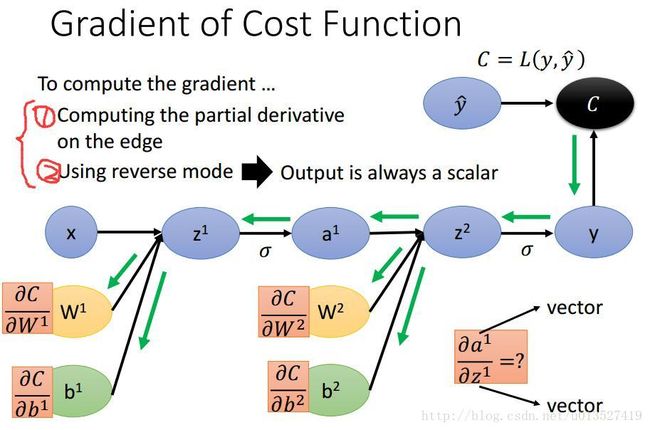
在计算的过程中，可见要用到一个向量y对另一个向量x的偏导数，此处用雅各布矩阵表示。矩阵的长为x的维数，高为y的维数，如下所示。

所以接下来依次计算计算图中每一条边上的偏导数。
（1）首先计算loss function对输出y的偏导数。一个常量C对一个向量y的偏导数为长为y的维数，高为1（C的维数）。下图中以分类问题为例，用的loss function 为交叉熵。

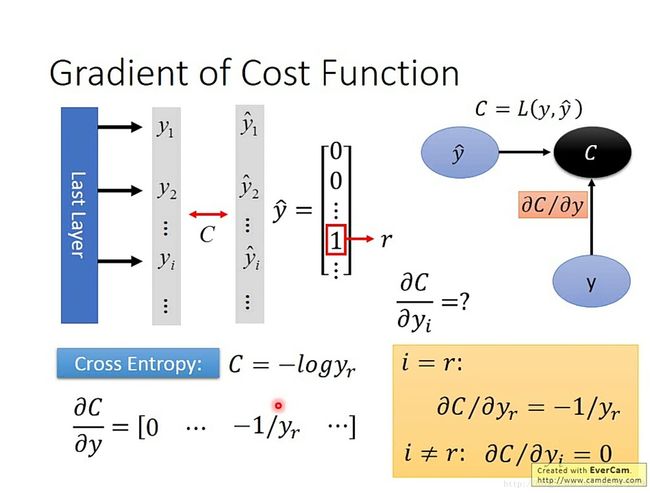
（2）计算神经元的输出y对输入z的偏导，激活函数以sigmoid为例，手画了一下帮助理解。

很明显，如果激活函数是换成softmax的话，那么z的每一维都会影响到y，就不是对角阵了。可以看看这篇文章【2】

（3）计算第l层神经元z对第l-1层的输出a的偏导数（简单）和第l层的权重w的偏导数（是一个tensor，形式上不好写）。

所以：

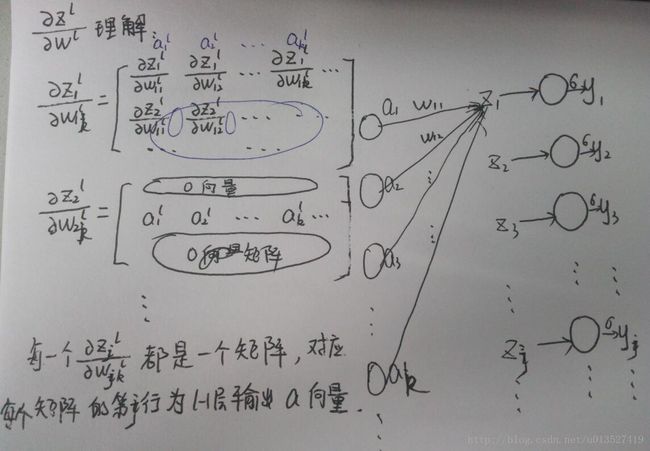
（4）重复计算（2）和（3），得到所有的边上的偏导数值，不管是求C对哪一个参数的偏导数，将改路径上每条边上的偏导数值相乘即可，这样就得到了最终的结果。

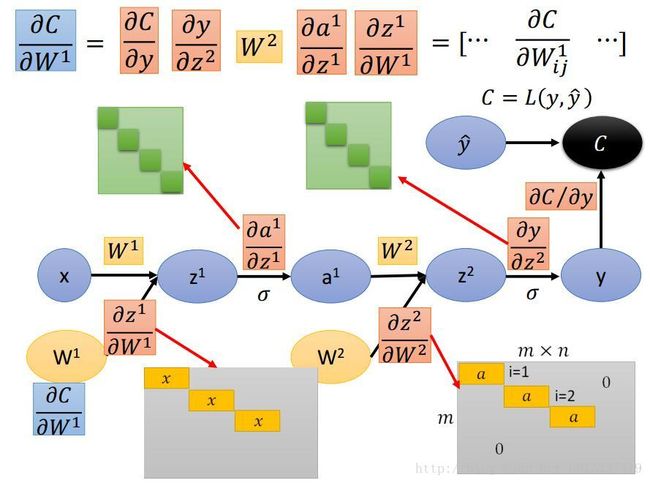
3.问题：

（1）图中的a的值还是需要前向传播算出来的。
（2）结果相同。

三、对其他结构的神经网络，思想和步骤是相同的。

【1】视频教程：http://www.bilibili.com/video/av9770302/index_4.html 台大李宏毅老师2017年的深度学习课程。
【2】通俗详解softmax函数及其求导过程