激光 2D SLAM 学习

激光 2D SLAM

本文主要介绍的是基于激光雷达的 2D SLAM，以及我最近看的粒子滤波、GMapping、Cartographer 等内容。

什么是 SLAM

图 1. cartographer 建的地图

全称 simultaneous localization and mapping，顾名思义，就是在机器人构建周围环境的地图的同时，定位它在地图中的位置。

算法的输入一般是：机器人对周围环境的观测信息 z (激光雷达的扫描点、摄像头的图像等) 和 机器人的控制信息 u (运动过程中的前进转向等信息，一般对其积分后用里程计 odometry 来表示)；

算法的输出是：机器人的运动轨迹 x 和 周围的地图 m 。

而我们要做的就是在给定 z 和 u 的条件下估计出 x 和 m：

p(x,m|z,u) p ( x , m | z , u )

这里我觉得可以稍微说一下为什么要用一个条件概率以及为什么可以用一个条件概率来表示我们的问题，因为在一开始接触机器人的时候我自己就有这样的疑惑。

首先为什么要用一个条件概率而不是一个封闭式的函数？因为我们无法对整个系统精确建模，或者说精确建模的代价太高，比如说传感器自身的测量误差（一般由厂家提供）、传感器与环境交互时的误差（激光雷达遇强光或黑色物体时的测量误差、摄像头在黑暗条件下的图像不清晰）等等，这都使我们很难用一个封闭式的函数求得一个解析解，所以我们只能用概率形式来表示在存在各种误差的情况下，使用 z 和 u 来估计 x 和 m 的分布。并且在 2d SLAM 中， x 就是一个 [x,y, [ x , y , \theta ] ] 的三维随机变量， 如果 m 是栅格地图， m 就是一个 r∗c r ∗ c 维的随机变量，其中 r r 是地图的宽度， c c 是地图的长度，所以我们可以用一个条件概率来解决我们的问题。实际上，在与传感器相关的问题中，很多问题都可以通过构建一个这样的条件概率、后验概率来求解。

难点

我们现在已经知道了 SLAM 问题应该如何表示了，那么还有什么难点在其中呢？难点就在于 x 和 m 之间是相互依赖的，也就是说：

1. 要想建图，我们需要知道机器人在各个时刻的精确轨迹信息
2. 要想获取精确的轨迹信息，我们需要借助精确的地图来定位

这也就是鸡生蛋问题。那这如何解决呢？对我们之前的 SLAM 后验分解一下看看：

图 2. 条件概率

其中建图那一项根据马尔科夫性质省略了 u0:t−1 u 0 : t − 1 ，因为在已知轨迹和观测信息的情况下，控制信息对于我们的建图而言是没有影响的。这样分解的实际意义就是，先根据测量信息和控制信息计算出机器人的轨迹，然后根据轨迹和测量信息建图。其实目前大部分 SLAM 算法都按照这个思路来实现的，并且主要关注于对运动轨迹的估计和优化上，因为有了精确的轨迹，建图就成了自然而然的事了。

地图的种类

在继续介绍 SLAM 的求解之前，我们先来介绍一下 SLAM 构建的地图的种类。

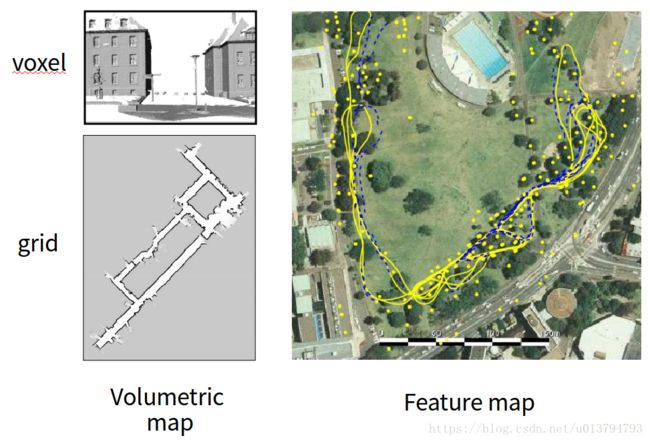
我所知道的 SLAM 构建的地图一般有两类：volumetric map 和 feature map

图 3. 地图种类

其中 feature map 我没有接触过，我理解的就是在测量信息中提取特征，将这些特征设置为 landmark ，并标示这些 landmark 的位置。这个地图的好处是比较适合动态的场景，因为当 landmark 移动到另一处时，我们只需要改变这个 landmark 的坐标就可以了。

虽然我接触的一直是 volumetric map ，但我还真不知道这该怎么翻译，不过在 2d 中， volumetric map 就是 grid map，也就是栅格地图， 3d 中就是 voxel map，也就是体素地图。因为本文主要讲的是 2d SLAM ，所以我还是主要讲一下栅格地图。

图 4. 栅格地图

栅格地图主要就是把地图离散化为一个个的单元(cell)，每个单元占据 r∗r r ∗ r 个像素，所以 r r 的大小就代表了地图的分辨率，位置在 (xi,yi) ( x i , y i ) 的 cell 的 index 为 i=xi∗y+yi i = x i ∗ y + y i 。

Assumption：

1. 每个 cell 有两种状态：free、occupied
2. 每个 cell 之间的状态相互独立

当 cell 为 free 时，该 cell 的灰度值就设为 255，也就是白色，当 cell 为 occupied 时，该 cell 的灰度值就设为 0 ，也就是黑色。初始时我们不知道 cell 具体的状态，我们就将其设为 100 ，也就是灰色。

接下来我们设 mi m i 为第 i i 个 cell 是否occupied 的随机变量，那么 p(mi=1) p ( m i = 1 ) 或 p(mi) p ( m i ) 就表示第 i i 个 cell 为 occupied 的概率，所以 p(mi)=1 p ( m i ) = 1 就表示第 i i 个 cell 为 occupied ， p(mi)=0 p ( m i ) = 0 就表示第 i i 个 cell 为 free ，如下图 5 ：

图 5. assumption 1

根据 assumption 2 ，我们很容易能得到下式：

p(m)=∏ip(mi) p ( m ) = ∏ i p ( m i )

图 6. assumption 2

有了这些基础概念，我们接下来就可以介绍各种具体的 SLAM 算法了。

已知轨迹的条件下建图

这里我们先介绍一下如何在已知轨迹的条件下建图。也就是在给定传感器数据 z1:t z 1 : t 和轨迹信息 x1:t x 1 : t 的条件下估计 t t 时刻的地图 m m ，即 p(m|z1:t,x1:t) p ( m | z 1 : t , x 1 : t ) 。上节我们说过，各个 cell 之间的状态是相互独立的，所以我们能够得到：

p(m|z1:t,x1:t)=∏ip(mi|z1:t,x1:t) p ( m | z 1 : t , x 1 : t ) = ∏ i p ( m i | z 1 : t , x 1 : t )

也就是我们单独的为每个 cell 计算 p(mi|z1:t,x1:t) p ( m i | z 1 : t , x 1 : t ) 即可。这里介绍一种最简单的方法——基于频率的方法——帮助我们快速理解这一计算过程。

首先定义各种用到的各种变量：

mit m t i ：第 i i 个 cell 在 t t 时刻是否被 occupied

vit v t i ：第 i i 个 cell 被观测的次数，也就是被激光扫描到的次数

bit b t i ：观测到第 i i 个 cell 被 occupied 的次数

p(mit) p ( m t i ) 的计算如下所示

---

每当接收到一次观测数据时，计算

(bit,vit)={(bit−1+1,vit−1+1)(bit−1,vit−1+1)ifoccupiediffree ( b t i , v t i ) = { ( b t − 1 i + 1 , v t − 1 i + 1 ) i f o c c u p i e d ( b t − 1 i , v t − 1 i + 1 ) i f f r e e

p(mit)=bitvit p ( m t i ) = b t i v t i

---

基于频率的方法比较简单粗暴，缺点是对 cell 的初始状态考虑不足。

《Probabilistic Robotics》 C9.2 介绍了更通用的算法来计算 p(mi|z1:t,x1:t) p ( m i | z 1 : t , x 1 : t ) ，这里就先不介绍了，书上说的也比较明白。

总之，我们需要知道的就是，在已知运动轨迹的条件下进行建图是比较简单的， SLAM 真正的难点应该是估计机器人的运动轨迹，也可以说是估计某时刻的位置。

已知地图的条件下预测轨迹

这一节介绍一下如何在已知地图的条件下预测机器人的运动轨迹，也就是 p(x1:t|z1:t,u0:t−1) p ( x 1 : t | z 1 : t , u 0 : t − 1 ) ，也许你会有个疑问：不是说先预测轨迹，才有地图的么，怎么这里能用地图信息来预测轨迹呢？而且这里的条件概率里也没有以地图信息作为条件啊。

这里我们将要求解的式子稍微改变一下，改为求

p(xt|xt−1,mt−1,zt,ut−1) p ( x t | x t − 1 , m t − 1 , z t , u t − 1 )

也就是在已知 t−1 t − 1 时刻的机器人位置、地图和控制信息，以及 t t 时刻的观测信息的条件下，估计 t t 时刻的机器人位置。其实这个式子跟之前那个是一样的，只不过一个估计的是轨迹，一个估计的是下一时刻的位置，实际上大多数 SLAM 都是迭代式的估计下一时刻的位置来进行建图的。接下来我就介绍一下粒子滤波是如何应用到机器人的位置估计的。

首先我们需要的其实就是能够得到上式的概率密度函数，然后找到使该概率密度函数取最大值时的 xt x t ，但是这个概率密度函数很难直接求解，于是人们就想到了用蒙特卡洛的方法通过样本来近似这个分布，进而求出 xt x t 。这也就是基于蒙特卡洛的定位算法。

这里先通过图示来大致介绍一下蒙特卡洛方法是如何帮助机器人定位的。

图 8. 蒙特卡洛定位

蒙特卡洛方法其实就是通过样本来近似概率分布。如图 8.a ，在没有任何观测数据的时候，机器人完全不知道自己在地图中的什么位置，因此此时它的位置在地图中应该是一个均匀分布，那我们就随机在地图中选取 100 个样本，各个样本的位置如图 8.a 的下图所示。

但好在我们的机器人有“一双眼睛”，可以看到自己目前是在一扇门的前面，那么我们就可以对每个样本计算从该位置看到的门与机器人“眼睛”看到的门的匹配程度了，匹配程度越高，我们也就为该样本赋予更高的权重，如图 8.b 的下图所示。

然后我们根据每个样本的权重对所有样本进行有放回的重新采样，直观上来说，我们应该能想到在三个门附近的样本数会更多一些，其他地方的样本数会比之前均匀分布的要少一些，也就是如图 8.c 的下图所示。不过这里的图 8.c 是机器人往右移动了一段距离后的图像，因此你会看到下图中三个门附近的样本都往右平移了一段距离。

现在机器人又看到自己在一个门的前面了，跟之前的操作一样，我们还是对每个样本计算它在地图中的匹配程度，匹配程度越高，我们就赋予该样本更高的权重，然后根据权重重新采样，不断重复这一过程。移动一段距离之后这些样本就能大致收敛到一处了，机器人也就能大概知道自己在地图中的位置了。

图 9 就是一个采用蒙特卡洛定位的真实例子，图中的黑点是一个样本，也就是一个位置估计，在运动到图 c 的位置时，位置估计就比较准确了。

图 9. 蒙特卡洛定位实例

这里给出蒙特卡洛定位的算法：

图 10. 蒙特卡洛定位算法

这里的 χ χ 就是所有的样本集，算法背后的数学原理如图 11 所示。

图 11. 贝叶斯分解

其中 measurement_model 就是计算图 11 中 observation likelihood，算法中没有计算 normalizer 的部分，这是因为每个样本的权重会标准化为 Σwi=1 Σ w i = 1 ，而 normalizer 与 xt x t 无关，所以在标准化时会被抵消掉，不需要计算。

参考资料

Probabilistic Robotics. S.Thrun

grid-maps：http://ais.informatik.uni-freiburg.de/teaching/ws15/mapping/pdf/slam10-gridmaps.pdf

RBPF：http://webdiis.unizar.es/~neira/5007439/stachniss-rbpfmapping.pdf