weixin_30314793

泰坦尼克号生还率预测分析

Titanic Data Analysis Report

数据源：https://pan.baidu.com/s/1r1fIJ6nIxisz8HA3hBa2kg

一、背景介绍

泰坦尼克号（RMS Titanic）是一艘奥林匹克级邮轮，于1912年4月处女航时撞上冰山后沉没。泰坦尼克号由位于爱尔兰岛贝尔法斯特的哈兰德与沃尔夫造船厂兴建，是当时最大的客运轮船。在她的处女航中，泰坦尼克号从英国南安普敦出发，途经__法国瑟堡-奥克特维尔以及爱尔兰昆士敦__，计划中的目的地为美国纽约。1912年4月14日，船上时间夜里11点40分，泰坦尼克号撞上冰山；2小时40分钟后，即4月15日凌晨2点20分，船裂成两半后沉入大西洋。泰坦尼克号海难为和平时期死伤人数最惨重的海难之一，同时也是最为人所知的海上事故之一。本案例旨在预测乘客生存的机会。

二、字段说明

本数据来源于kaggle,包括训练集（892条数据，12个纬度），测试集（418条数据，11个纬度，是否存活这条变量需要预测）

变量说明表

三、描述性分析

导入模块


# Titanic Data Analysis Report

# 导入和数据处理相关的模块
import pandas as pd

import numpy as np

# 导入和绘图相关的模块

from matplotlib import pyplot as plt

import seaborn as sns

# 导入和机器学习相关的模块

from sklearn.tree import DecisionTreeClassifier,DecisionTreeRegressor

# 从决策树模块中导入分类决策树和回归决策树

# 导入警告

import warnings

warnings.filterwarnings('ignore')
# 忽略警告


# 读取数据
train = pd.read_csv('train.csv')

test = pd.read_csv('test.csv')

real = pd.read_csv('gender_submission.csv')

查看训练集，测试集以及真实数据的形状

train.shape,test.shape,real.shape

((891, 12), (418, 11), (418, 2))

train.head()  # 展示训练数据的前五行

test.tail()   # 展示测试数据的后五行

print(test.info())  # 查看数据详细信息

# 通过处理查看训练集数据的缺失情况

# 统计训练集中数据的缺失情况，并按照降序进行排列

total = train.isnull().sum().sort_values(ascending=False)

percent = round(train.isnull().sum().sort_values(ascending=False)/len(train)*100,2)

pd.concat([total,percent],axis=1,keys=['Total','Percent'])

# 可见训练集在仓位这一变量中缺失值严重，达到77%。

# 通过统计查看测试集数据的缺失情况 

total = test.isnull().sum().sort_values(ascending=False)

percent = round(test.isnull().sum().sort_values(ascending=False)/len(test)*100,2)

pd.concat([total,percent],axis=1,keys=['Total','Percent'])

绘制是否存活人数的柱形图

# 统计是否存活人数的频率分布直方图
print(train.Survived.value_counts())   # 统计是否存活的人数分布
sns.countplot(x='Survived',data=train)
plt.show()

0 549
1 342
Name: Survived, dtype: int64

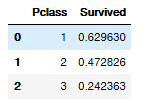
# 找出train中的Pclass与Survived,利用Pclass进行分组，并对是否存活的均值进行排序
train[['Pclass','Survived']].groupby(['Pclass'],as_index=False).mean().sort_values(by='Survived',ascending=False)

绘制性别与存活概率的柱形图

# 性别与是否存活的关系
pal = {'male':"skyblue", 'female':"Pink"}
plt.subplots(figsize=(13,8))
ax = sns.barplot(x='Sex',
                 y='Survived',
                 hue='Sex',
                 data=train,
                 palette=pal,
                 linewidth=2 )
plt.xlabel("Sex",fontsize=15)
plt.ylabel('% of passenger survived',fontsize=15)
plt.title('Survived/Non-Survived Passenger Gender Distribution',fontsize=15)
plt.show()

绘制性别与是否存活的关系图

# 有多少的男性和女性存活
print(train.groupby('Sex')['Survived'].sum())
print(train.Sex.value_counts())
sns.countplot(x='Survived',hue='Sex',data=train)
plt.show()
# 根据统计的结果发现，女性74%  ，男性18%

Sex
female 233
male 109
Name: Survived, dtype: int64
male 577
female 314
Name: Sex, dtype: int64

绘制是否存活与票价的关系图

# 是否存活于票价之间的关系
sns.set(style='ticks')
sns.boxplot(x='Survived',y='Fare',hue='Survived', data=train,palette='PRGn')
sns.despine(offset=10,trim=True)
plt.show()

# 船票与死亡的进一步探究
fareplt=sns.FacetGrid(train,hue='Survived',aspect=5)
fareplt.map(sns.kdeplot,'Fare',shade=True)
fareplt.set(xlim=(0,train.Fare.max()))
fareplt.add_legend()
plt.show()
# 船票在0-20岁死亡的人数明显大于存活的人数

绘制是否存活与年龄的关系图

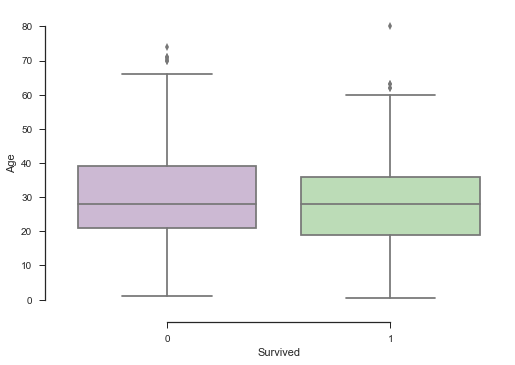
sns.set(style='ticks')
sns.boxplot(x='Survived',y='Age', data=train,palette='PRGn')
sns.despine(offset=10,trim=True)
plt.show()
# 训练数据集中是够存活和年龄的关系不是不明显

绘制年龄与是否存活的概率关系图

# 对年龄进行进一步分析,发现年龄在0-10之间的存活的人数大于死亡的人数
ageplt=sns.FacetGrid(train,hue='Survived',aspect=4)
ageplt.map(sns.kdeplot,'Age',shade=True)
ageplt.set(xlim=(0,train.Age.max()))
ageplt.add_legend()
plt.show()

社会地位与是否存活的频数关系图

# 是否存活与社会经济地位之间的关系  1低 2中 3高
print(train.groupby('Pclass')['Survived'].sum())
print(train.groupby('Pclass')['Survived'].mean())
sns.countplot(x='Survived',hue='Pclass',data=train)
plt.show()

Pclass
1 136
2 87
3 119
Name: Survived, dtype: int64
Pclass
1 0.629630
2 0.472826
3 0.242363
Name: Survived, dtype: float64

是否存活与船上兄弟姐妹以及配偶的数量频数关系图

# 是否存活与船上兄弟姐妹以及配偶的数量
print(train.groupby('SibSp')['Survived'].sum())
sns.countplot(x='Survived',hue='SibSp',data=train)
plt.legend(loc=1)   #移动标签颜色的位置 ，1代表右上角
plt.show()

SibSp
0 210
1 112
2 13
3 4
4 3
5 0
8 0
Name: Survived, dtype: int64

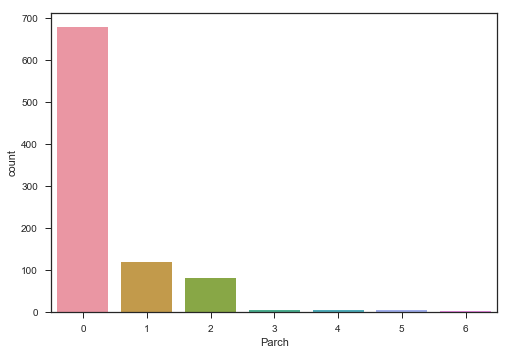
船上双亲以及儿女数量的频数分布图

# 该乘客在船上的双亲以及儿女的数量频数分布图
print(train.Parch.value_counts())
sns.countplot(x='Parch',data=train)
plt.show()

0 678
1 118
2 80
5 5
3 5
4 4
6 1
Name: Parch, dtype: int64

是否存活与该乘客在船上的双亲以及儿女数量的频数分布图

#是否存活与该乘客在船上的双亲以及儿女的数量
print(train.groupby('Parch')['Survived'].sum())
sns.countplot(x='Survived',hue='Parch',data=train)
plt.legend(loc=1) #moving the legned to the right
plt.show()

Parch
0 233
1 65
2 40
3 3
4 0
5 1
6 0
Name: Survived, dtype: int64

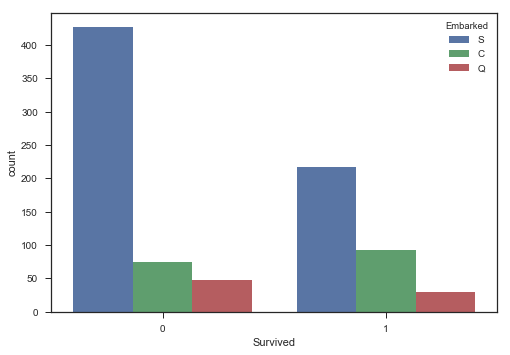
是否存活与船上位置之间的频数分布图

# 是否存活与船上的位置之间的关系
print(train.Embarked.value_counts())  # 分类统计频数使用value_counts()
print(train.groupby('Embarked')['Survived'].sum())
print(train.groupby('Embarked')['Survived'].mean())
sns.countplot(x='Survived',hue='Embarked',data=train)
plt.show()

S 644
C 168
Q 77
Name: Embarked, dtype: int64
Embarked
C 93
Q 30
S 217
Name: Survived, dtype: int64
Embarked
C 0.553571
Q 0.389610
S 0.336957
Name: Survived, dtype: float64

数据处理以及转换

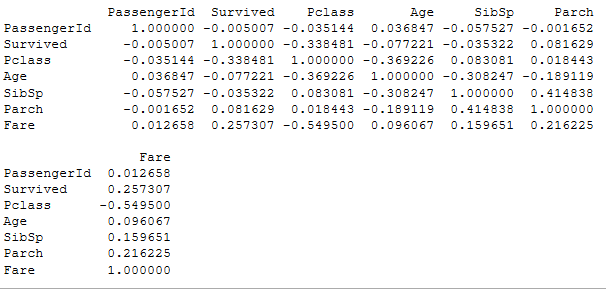
print(train.corr())    # 计算各个变量之间的关系

# 探究姓名
train["title"] = [i.split('.')[0] for i in train.Name]
train["title"] = [i.split(',')[1].strip() for i in train.title]
print(train.title.value_counts())
# print(train.groupby('title')['Survived'].sum())
# 绘制性别与是否存活的关系
# sns.countplot(x='Survived',hue='title',data=train)
# plt.show()

是否存活与乘客地位的频数分布图

# 进一步探究
train["title"] = [i.replace('Mr', 'Mr') for i in train.title]
train["title"] = [i.replace('Ms', 'Miss') for i in train.title]
train["title"] = [i.replace('Mlle', 'Miss') for i in train.title]
train["title"] = [i.replace('Mme', 'Mrs') for i in train.title]
train["title"] = [i.replace('Dr', 'rare') for i in train.title]
train["title"] = [i.replace('Col', 'rare') for i in train.title]
train["title"] = [i.replace('Major', 'rare') for i in train.title]
train["title"] = [i.replace('Don', 'rare') for i in train.title]
train["title"] = [i.replace('Jonkheer', 'rare') for i in train.title]
train["title"] = [i.replace('Sir', 'rare') for i in train.title]
train["title"] = [i.replace('Lady', 'rare') for i in train.title]
train["title"] = [i.replace('Capt', 'rare') for i in train.title]
train["title"] = [i.replace('the Countess', 'rare') for i in train.title]
train["title"] = [i.replace('Rev', 'rare') for i in train.title]
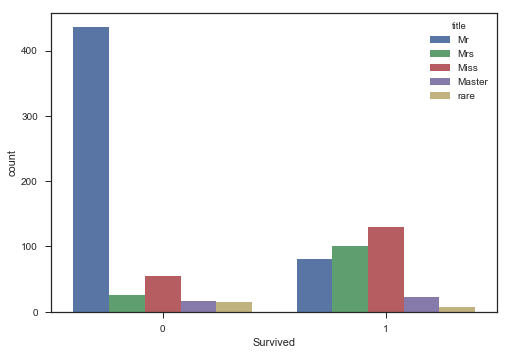
print(train.title.value_counts())
sns.countplot(x='Survived',hue='title',data=train)
plt.show()

Mr 517
Miss 185
Mrs 126
Master 40
rare 23
Name: title, dtype: int64

test["title"] = [i.split('.')[0] for i in test.Name]
test["title"] = [i.split(',')[1].strip() for i in test.title]
print(test.title.value_counts())

# 进一步探究
test["title"] = [i.replace('Mr', 'Mr') for i in test.title]
test["title"] = [i.replace('Ms', 'Miss') for i in test.title]
test["title"] = [i.replace('Mlle', 'Miss') for i in test.title]
test["title"] = [i.replace('Mme', 'Mrs') for i in test.title]
test["title"] = [i.replace('Dr', 'rare') for i in test.title]
test["title"] = [i.replace('Col', 'rare') for i in test.title]
test["title"] = [i.replace('Major', 'rare') for i in test.title]
test["title"] = [i.replace('Don', 'rare') for i in test.title]
test["title"] = [i.replace('Jonkheer', 'rare') for i in test.title]
test["title"] = [i.replace('Sir', 'rare') for i in test.title]
test["title"] = [i.replace('Lady', 'rare') for i in test.title]
test["title"] = [i.replace('Capt', 'rare') for i in test.title]
test["title"] = [i.replace('the Countess', 'rare') for i in test.title]
test["title"] = [i.replace('Rev', 'rare') for i in test.title]
test["title"] = [i.replace('rarea', 'rare') for i in test.title]
print(test.title.value_counts())
test.head()

Mr 240
Miss 79
Mrs 72
Master 21
rare 6
Name: title, dtype: int64

变量相关系数图

mask = np.zeros_like(train.corr(), dtype=np.bool)  
# 创建一个和数据的每列相关系数对比的二维矩阵
mask[np.triu_indices_from(mask)] = True

plt.subplots(figsize = (15,12))
sns.heatmap(train.corr(), 
            annot=True,
            mask = mask,
            cmap = 'RdBu_r',
            linewidths=0.1, 
            linecolor='white',
            vmax = .9,
            square=True)
plt.title("Correlations Among Features", y = 1.03,fontsize = 20)
plt.show()

可见是否存活与票价成正相关

Fare and Survived: 0.26

存在负相关变量

Fare and Pclass: -0.6

Sex and Survived: -0.55

Pclass and Survived: -0.33

train.describe()  # 对数据进行描述

建立模型，在判断是否存活的问题上，我们可以想到的模型有：逻辑回归，XGBoost SVM 决策树随机森林 KNN 高斯朴素贝叶斯 voting Classifer将多个模型的结果通过投票的方式进行聚合

四、建立模型

from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import confusion_matrix# 绘制混淆矩阵需要使用的模块

建模前处理数据

train = train.drop(['Name', 'PassengerId','Ticket','Cabin'], axis=1)  # 删除编号和名字两列
test = test.drop(['Name','Ticket','Cabin'], axis=1)  # 删除测试集中的名字列
combine = [train, test]
train.shape, test.shape

((891, 9), (418, 9))

print(train.head())

print(test.head())

for dataset in combine:
    dataset['Sex'] = dataset['Sex'].map( {'female': 1, 'male': 0} ).astype(int)

train.head()

print(test.shape)
print(test['title'].value_counts())
print(train['title'].value_counts())

(418, 9)
Mr 240
Miss 79
Mrs 72
Master 21
rare 6
Name: title, dtype: int64
Mr 517
Miss 185
Mrs 126
Master 40
rare 23
Name: title, dtype: int64

# for dataset in combine:
#     dataset['title'] = dataset['title'].fillna(0)
for dataset in combine:
#     dataset.dropna()
    dataset['title'] = dataset['title'].map({'Mr': 1, 'Miss': 2, 'Mrs': 3, 'Master':4, 'Rare': 5})

for dataset in combine:
    dataset['Embarked'] = dataset['Embarked'].map({'S': 1, 'C': 2, 'Q': 3})

for dataset in combine:    
    dataset.loc[ dataset['Age'] <= 16, 'Age'] = 0
    dataset.loc[(dataset['Age'] > 16) & (dataset['Age'] <= 32), 'Age'] = 1
    dataset.loc[(dataset['Age'] > 32) & (dataset['Age'] <= 48), 'Age'] = 2
    dataset.loc[(dataset['Age'] > 48) & (dataset['Age'] <= 64), 'Age'] = 3
    dataset.loc[ dataset['Age'] > 64, 'Age'] = 4
print(train.head())
print(test.head())

方法一：逻辑回归

train = train.dropna()
test = test.dropna()
X_train = train.drop("Survived", axis=1)
# X_train.dropna()
Y_train = train["Survived"]
# Y_train.dropna()
X_testid = pd.DataFrame(test["PassengerId"])
X_test  = test.drop("PassengerId", axis=1).copy()
# X_test.dropna()
X_train.shape, Y_train.shape, X_test.shape,X_testid.shape

((690, 8), (690,), (325, 8), (325, 1))

# 导入逻辑回归模块
from sklearn.linear_model import LogisticRegression
# 构建一个逻辑回归模型对象
logic = LogisticRegression()
# 第一个值为特征数据，第二个值为目标数据
logic.fit(X_train,Y_train)
Y_pred = pd.DataFrame(logic.predict(X_test))
type(Y_pred),type(X_testid)

(pandas.core.frame.DataFrame, pandas.core.frame.DataFrame)

Y_pred.head()

X_testid.head()

# 合并
df = pd.merge(X_testid,Y_pred,left_index=True,right_index=True)
df.head()

real.head()

realdf = pd.merge(df,real,left_on='PassengerId',right_on='PassengerId')
realdf.head()

# 修改列名，传入的参数必须是字典格式
realdf = realdf.rename(columns={'PassengerId':'id',0:'pre','Survived':'real'})
print(realdf.shape)
realdf.head()

(249, 3)

# 准确率
acc_log = round(logic.score(X_train, Y_train) * 100,3)
print(realdf['real'].value_counts())
print('*'*30)
print('预测的准确率：',acc_log)

0 153
1 96
Name: real, dtype: int64
******************************
预测的准确率： 82.899

根据真实数据绘制混淆矩阵表

# confusion_matrix该函数中传入的参数为（真实数据，预测数据，标签）
c=confusion_matrix(realdf['real'],realdf['pre'],labels=[0,1])
c

array([[86, 67],
[48, 48]])

混淆矩阵表

print(realdf.loc[realdf['pre']==realdf['real']].count())  # 预测正确的次数
realdf.loc[realdf['pre']!=realdf['real']].count()    # 预测错误的次数
# 预测正确的概率
round(134/249,2)

id 134
pre 134
real 134
dtype: int64

0.54

方法二：支持向量机

svc = SVC()
svc.fit(X_train, Y_train)
Y_pred = svc.predict(X_test)
acc_svc = round(svc.score(X_train, Y_train) * 100, 1)
print('*'*30)
print('预测的准确率：',acc_svc)

预测的准确率： 87.5

方法三：KNN

knn = KNeighborsClassifier(n_neighbors = 3)
knn.fit(X_train, Y_train)
Y_pred = knn.predict(X_test)
acc_knn = round(knn.score(X_train, Y_train) * 100, 2)
print('*'*30)
print('预测的准确率：',acc_knn)

预测的准确率： 88.12

方法四：朴素贝叶斯

gaussian = GaussianNB()
gaussian.fit(X_train, Y_train)
Y_pred = gaussian.predict(X_test)
acc_gaussian = round(gaussian.score(X_train, Y_train) * 100, 2)
print('*'*30)
print('预测的准确率：',acc_gaussian)

预测的准确率： 81.45

方法五：感知器二元分类器的监督学习算法

perceptron = Perceptron()
perceptron.fit(X_train, Y_train)
Y_pred = perceptron.predict(X_test)
acc_perceptron = round(perceptron.score(X_train, Y_train) * 100, 2)
print('*'*30)
print('预测的准确率：',acc_perceptron)

预测的准确率： 68.7

方法六：线性的svc

linear_svc = LinearSVC()
linear_svc.fit(X_train, Y_train)
Y_pred = linear_svc.predict(X_test)
acc_linear_svc = round(linear_svc.score(X_train, Y_train) * 100, 2)
print('*'*30)
print('预测的准确率：',acc_linear_svc)

预测的准确率： 82.32

方法七：随机梯度下降

sgd = SGDClassifier()
sgd.fit(X_train, Y_train)
Y_pred = sgd.predict(X_test)
acc_sgd = round(sgd.score(X_train, Y_train) * 100, 2)
print('*'*30)
print('预测的准确率：',acc_sgd)

预测的准确率： 77.97

方法八：决策树

decision_tree = DecisionTreeClassifier()
decision_tree.fit(X_train, Y_train)
Y_pred = decision_tree.predict(X_test)
acc_decision_tree = round(decision_tree.score(X_train, Y_train) * 100, 2)
print('*'*30)
print('预测的准确率：',acc_decision_tree)

预测的准确率： 94.78

方法九：随机森林

random_forest = RandomForestClassifier(n_estimators=100)
random_forest.fit(X_train, Y_train)
Y_pred = random_forest.predict(X_test)
random_forest.score(X_train, Y_train)
acc_random_forest = round(random_forest.score(X_train, Y_train) * 100, 2)
print('*'*30)
print('预测的准确率：',acc_random_forest )