利用MATLAB仿真最小发射功率下WSN的连通性和覆盖率

一、目的

     （1）在固定节点个数的前提下，仿真求得使网络保持连通的最小通信半径（最低能级）。

     （2）在上述节点个数和通信半径的前提下，计算随机布撒的节点的覆盖率。

二、方法描述

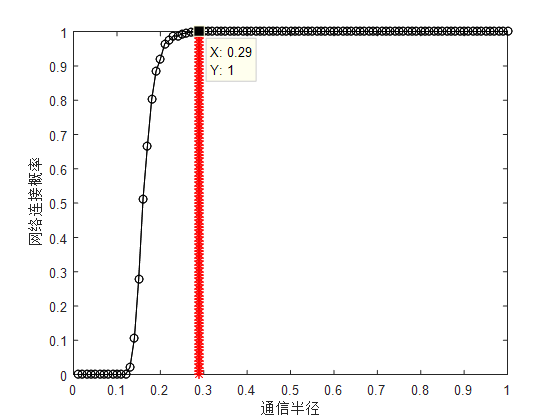
       （1）首先假设通信半径都等于感知半径，并且每个节点发射功率均相同。在1x1的单位矩形中随机部署100个传感器节点，在每一节点通信半径下进行1000次试验，进而模拟出连通率随通信半径增加的变化趋势。得出在1000点下保持网络连通的最小通信半径。

        从上图可以得出，每个节点得最小通信半径为r=0.29。

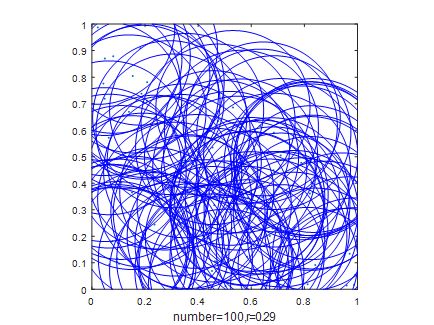
     （2）通过一次随机布撒100个节点，并以每个节点为圆心，绘出半径为0.29的圆。如下图所示：

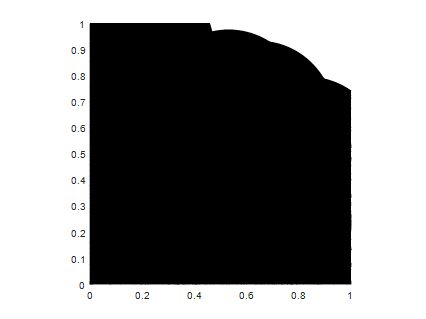
         开始想利用微元的思想，将1x1的区域划分成100个小方格，但之后发现该方法复杂。实验中采用将每个节点的圆（通信覆盖范围）填充为黑色，通过连通图中黑白像素点的比例得到覆盖率。覆盖图如下图所示：

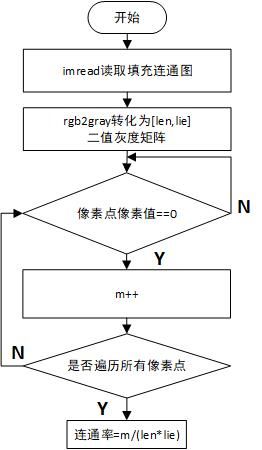
          算法实现流程图如下：

        试验中注意的是在得到网络的覆盖图之后，需要将其进行处理，仅将1x1的区域截出进行计算，否则实验结果会出现意外错误。

        实现重要程序如下：

pp=imread('C:\Users\zhangkun\Desktop\1.png')
p=rgb2gray(pp);
m=0;
len=size(p,1)
lie=size(p,2)
for i=1:len
    for j=1:lie
     if(p(i,j)==0)   
         m=m+1;
     end
    end
end
fugailv=m/(len*lie)%0.9346

三、结论

       在节点个数确定时，存在一个使网络保持连通的最小通信半径（最小能级），可以达到节约能量。本实验中选取100个节点随机布撒，通过1000次仿真得到网络的最小通信半径为0.29m，在该半径下一次随机布撒的覆盖率为93.46%。

四、程序代码

L=1;                    % 节点布置区域
theta=0:pi/100:2*pi; 
n=100;                             % 节点个数
node_max=0.29;                  % 节点最大通信距离
X=unifrnd(0,L,1,n);           % 生成n个均匀随机数作为横坐标
B=sqrt(L^2-abs(X).^2);     % 计算每个x对应的y范围
Y=unifrnd(0,B,1,n);          % 对每个横坐标生成均匀随机数作为纵坐标
plot(X,Y,'.')
hold on
axis equal;
axis([0 1 0 1]); 
figure(1)
for i=1:n
   hold on
   x=node_max*cos(theta)+X(i);
   y=node_max*sin(theta)+Y(i);
   plot(x,y,'b-')
    %fill(x,y,'k');
end
figure(2)
axis equal;
axis([0 1 0 1]); 
for i=1:n
   hold on
   x=node_max*cos(theta)+X(i);
   y=node_max*sin(theta)+Y(i);
   %plot(x,y,'k-')
   fill(x,y,'k');
end

pp=imread('C:\Users\kkzhang\Desktop\1.png')
p=rgb2gray(pp);
m=0;
len=size(p,1)
lie=size(p,2)
for i=1:len
    for j=1:lie
     if(p(i,j)==0)   
         m=m+1;
     end
    end
end
fugailv=m/(len*lie)%0.9346

生活中总有不期而遇的温暖与生生不息的希望！

转载需说明出处，笔者总结之前的知识，与大家分享，有问题的可以留给我哦~

 

 

 

 

转载于:https://www.cnblogs.com/lemonzhang/p/9254033.html