递归代码的时间复杂度分析起来非常麻烦,今天我们尝试来借助递归树分析递归算法的时间复杂度。
1. 递归树与时间复杂度分析
递归的思想就是将大问题一层一层地分解为小问题来求解,如果我们把这个分解过程画成图,它其实就是一棵树,我们称之为递归树。
上图为斐波那契数列的递归树,节点里的数字表示数据的规模,一个节点的求解可以分解为左右子节点两个问题的求解。
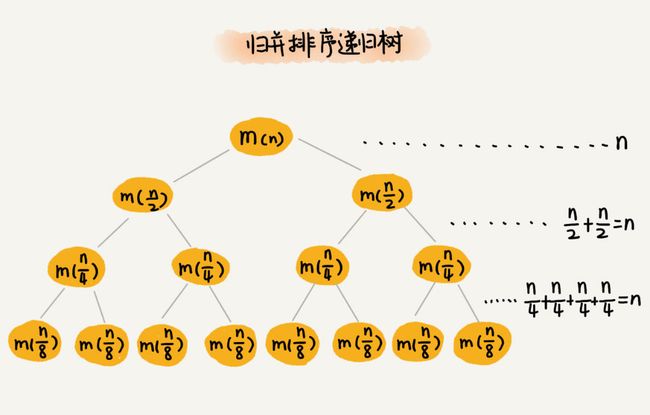
下面我们用递归树来分析一下归并排序的时间复杂度。归并排序每次都将数据分为左右两部分,然后将左右两部分排好序的数据再合并起来。
可以看到,归并排序大部分的时间都消耗在将两部分数据合并成一部分的归并操作上。而在树的每一层,可以看到,我们总共要归并的数据规模是一样的,都为 $n$。而且,这是一个满二叉树,树的高度大约为 $log_2n$。因此,归并排序的时间复杂度也就为 $O(nlog_2n) = O(nlogn)$。
2. 快速排序的时间复杂度
快速排序在最好的情况下,每次分区都恰好将数据一分为二,这时候递推公式为 $T(n) = 2T(\frac{n}{2})+n$,我们可以很容易地就推导出时间复杂度为 $O(nlogn)$。
但实际上,我们不可能每次都做到将数据恰好一分为二。假设每次两个分区的大小比例为 $1:k$,当 $k=9$ 时,递推公式就为 $T(n) = T(\frac{n}{10})+T(\frac{9n}{10})+n$,这时候推导起来就比较复杂了。
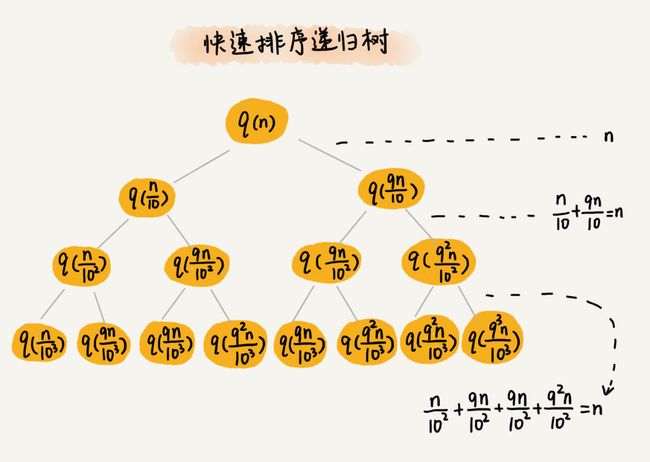
针对同样的情况,下面我们来看递归树的分析法。
可以看到,在快速排序的每一层,我们需要遍历的数据总数都为 $n$。接下来,我们只需要知道递归树的深度就可以得出时间复杂度了。
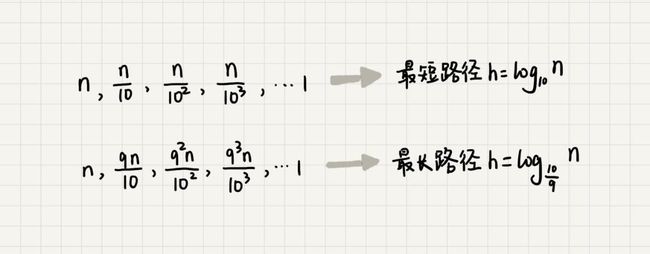
如果每次都乘以 $\frac{1}{10}$,那么树就会最快到达节点值为 1 的叶节点;而如果每次都乘以 $\frac{9}{10}$,那么树就会最慢到达节点值为 1 的叶节点,此即为树的最大深度。
因此快速排序的时间复杂度就介于 $O(nlog_{10}n)$ 和 $O(nlog_{\frac{10}{9}}n)$ 之间。而当 $k$ 变化的时候,也只是底数发生了变化,用大 $O$ 法表示的时间复杂度都为 $O(nlogn)$。
3. 斐波那契数列的时间复杂度
斐波那契数列的算法如下,我们可以很容易地建立一个递归树。
int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return f(n-1) + f(n-2);
}可以看到节点总数随着层数指数级增加,而每一层需要的加法次数与节点个数成正比,第 $k$ 层的时间消耗为 $2^{k-1}$。
如果每次都取 $n-1$,那么此时从根节点到叶节点路径最长,大约为 $n$;而如果每次都取 $n-2$,那么此时从根节点到叶节点路径最短,大约为 $\frac{n}{2}$。
因此,算法的时间复杂度就介于
$$O(min) =1+2+\cdots+2^{\frac{n}{2}-1} = 2^{\frac{n}{2}}-1$$
$$O(max) = 1+2+\cdots+2^{n-1} = 2^n-1$$
这样,我们就基本知道了这个算法的时间复杂度是指数级的,非常高。
4. 全排列的时间复杂度
求 $n$ 个数的全排列也可以借助递归来实现,如果我们确定了最后一位数据,那问题就变成了求解剩余 $n-1$ 个数据的全排列这个子问题。
假设数组中存储的是 1,2, 3...n。
f(1,2,...n) = {最后一位是 1, f(n-1)} + {最后一位是 2, f(n-1)} +...+{最后一位是 n, f(n-1)}。
写成代码如下:
// 调用方式:
// int[]a = a={1, 2, 3, 4}; printPermutations(a, 4, 4);
// k 表示要处理的子数组的数据个数
public void printPermutations(int[] data, int n, int k) {
if (k == 1) {
for (int i = 0; i < n; ++i) {
System.out.print(data[i] + " ");
}
System.out.println();
}
for (int i = 0; i < k; ++i) {
int tmp = data[i];
data[i] = data[k-1];
data[k-1] = tmp;
printPermutations(data, n, k - 1);
tmp = data[i];
data[i] = data[k-1];
data[k-1] = tmp;
}
}同样,我们也可以画出这个算法的递归树,只不过这个树已经不是标准的二叉树了。
第一层我们需要 $n$ 次数据交换,第二层有 $n$ 个 $n-1$ 次数据交换,以此类推,第 $k$ 层数据交换总次数为 $n*(n-1)*(n-2)\cdots*(n-k+1)$。所以,算法总的时间复杂度为
n + n*(n-1) + n*(n-1)*(n-2) +... + n*(n-1)*(n-2)*...*2*1这个求和公式比较复杂,但我们知道最后一项为 $n!$,而前面的项都小于 $n!$,因此总和肯定介于 $1*n!$ 和 $n*n!$ 之间。算法的时间复杂度为阶乘级的,非常高。
参考资料-极客时间专栏《数据结构与算法之美》
获取更多精彩,请关注「seniusen」! ![]()