分享 | 关于人工智能算法建模稳定性那些事儿
背景
“建模”是算法、数据挖掘岗同学日常工作的一个重要部分。而建模流程中,非常重要同时又容易被大家忽视的一个环节就是稳定性问题。
市面上关于建模稳定性的文章不多,笔者决定与大家分享一下自己的经验。
本文是自己的一些实践经验分享,尽量做到让读者看过之后就可以动手实践。如果你之前从未进行过建模稳定性方面的关注,那么看过本篇分享后,取其中一二进行关注,相信能够达到事先规避一些潜在的问题的效果。关于建模稳定性方面本文未能涉及的地方,也欢迎大家踊跃在评论区补充和交流!
建模过程中的稳定性,一般包括特征稳定性和模型稳定性,下面依次介绍给大家介绍。
特征稳定性
所谓特征稳定性,就是关注该特征的取值随着时间的推移会不会发生大的波动。
对特征稳定性的关注,一定一定要在建模之前完成,从一开始就避免将那些本身不太稳定的特征选入模型。遗憾的是,很多做模型的同学并没有留意这一点,而是喜欢在特征ready后立刻开始建模,直到模型临近上线,才意识到应该去看看有没有不太稳定的特征,一旦发现有特征稳定性不满足要求,则需要对其进行剔除后重新建模,导致了不必要的重复性劳动。
通常采用PSI(PopulationStability Index,群体稳定性指数)指标评估特征稳定性。计算公式如下:
PSI是对两个日期的特征数据进行计算,可以任选其一作为base集,另一则是test集(也有其他叫法为expected集和actual集)。
下面介绍特征的PSI是如何计算出来的,有了这个,就可以读懂上面的公式了:
• 特征取值等频分段:对这个特征在base集的取值进行等频划分(通常等频分10份即可),用字母i表示第i个分段区间。
• 计算:![]()
统计落在每个分段区间内的目标数量(如果是用户特征就是用户数,如果是门店特征就是门店数,etc),进一步得到数量占比,![]()
表示该特征在base集中第i个取值分段中的数量占比。
• 计算:![]()
继续按照第2步计算得到![]()
,注意,分段还是采用第1步中产出的分段(依据base集产出的分段)。
• 根据前文的公式即可计算得到该特征基于这两个日期的PSI。
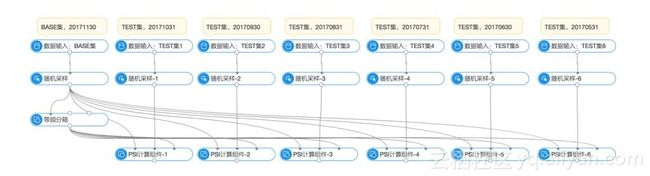
当没有其他工具可以借力的时候,根据上述流程便可轻松计算得到特征PSI。但是在蚂蚁金服,因为算法建模PAI平台的存在,直接借助所提供的PSI计算组件即可方便、批量地计算出特征PSI。
在上面这个例子中,我对上百个特征计算PSI,流程如下:
• 取20171130分区的数据作为base集,对所有特征通过分箱组件进行特征值等频分段(上述步骤1),分箱之前进行随机采样的目的是减少数据量以加快分箱进程。
• 计算20171130分区与过往六个月分区的特征PSI,这就是PSI组件做的事情,也就是前文所述步骤2~4。
通过这个流程,轻松计算得到了上百个特征跨度1个月~跨度6个月的PSI。通常,如果一个特征跨度6个月的PSI取值小于0.1,那么这个特征被认为是稳定的(当然,也可以根据具体情况适当放宽0.1的标准)。
注意:并非所有PSI值很高的特征都不能用于建模,如果一个特征区分度很好但PSI值不满足预期(比如跨度6个月的PSI大于0.1),但同时,该特征的取值波动性从业务的角度可以解释得通,那么这样的特征用于建模也是可以的。
模型稳定性
相比特征稳定性,模型稳定性涉及的东西比较多,需要根据模型的具体应用方式选择性进行关注。通常,模型PSI是必须关注的一个指标。
- 模型PSI
有了前文对特征PSI的介绍,理解模型PSI就非常简单了。
二分类模型的输出一般都会有一个取值为0~1之间的概率值(记作:prediction_prob),模型PSI监控的就是这个值的稳定性。
将模型产出的prediction_prob理解为一个特征,就可以像计算特征PSI一样计算得到模型PSI了,不同的地方在于,特征PSI一般是对很多特征一起做计算(假如准备了200个特征进行建模,那就是对200个特征计算PSI),而模型PSI通常只是对prediction_prob这一个字段做计算。计算方式同前文所述完全一样,PAI组件的使用也没有任何不同,不再赘述。
- 模型稳定性的其他实践
2.1 消除波动性
对于二分类模型,在实际业务中通常会直接拿着prediction_prob去用。例如,对于某个风险识别场景,根据prediction_prob对用户进行准入或拦截(假如设定阈值为0.6,则prediction_prob小于0.6的用户被拦截,不小于0.6的用户被准入)。
但是会存在一些应用场景对稳定性要求更高。为了消除double型可能带来的波动性,可以将小数映射为整数再使用,我们将这个过程称为Rank。
具体要将0~1的小数值映射到1~10还是1~100亦或是1~1000的整数区间,完全取决于应用场景对这个数值的精细化程度。这样做映射以消除波动性是有道理的,它相当于把一定范围内的波动屏蔽了。例如,某信用风险模型在10月份对用户小C的打分为0.61,在11月份的打分为0.69(假如打分的差异仅仅因为该用户在双11期间疯狂买买买所致,而事实上短暂性的买买买并不应该对用户的信用风险评估造成影响),如果映射为1~10的整数区间后,连续两个月份的打分都是7([0.6, 0.69]整个区间均被映射为7),从而达到屏蔽波动性的目的。
将0~1小数映射到整数区间的做法非常简单:首先对原始小数列求分位数(如果要映射为1~10的得分区间就求十个分位点,如果要映射为1~100的得分区间就求一百个分位点),然后根据各分位点处的取值将原始值分为确定数量的区间(如果要映射为1~10的得分区间就是10个区间,如果要映射为1~100的得分区间就是100个区间),每个区间映射为一个整数值,映射完毕。
2.2 Rank迁移
当把prediction_prob Rank到整数区间后,就有必要对Rank后的结果实施必要的监控了。有两个事情值得去做,其一是对分位点进行按月迁移监控(看分位点有没有随着时间的推移产生波动),其二是对Rank后的整数进行月份间波动监控(看看每连续两个月之间,全量用户得分的波动性)。
计算上文所述指标的目的是为了实施每日监控,一旦出现不符合预期的情况就立刻通知到人。在蚂蚁金服内部,可以借助相关平台实施所需的监控。当然,如果没有这样的平台,也可以通过其他的方式来做,比如:每日定时执行SQL语句来实施监控分析,并将执行结果做成报表以方便查看,等等。
以上内容任何疏漏之处,恳请不吝指正。欢迎大家补充自己对建模稳定性的实践之道!