Deep Learning Specialization课程笔记——超参数设定,批量标准化等
Hyperparameter tuning
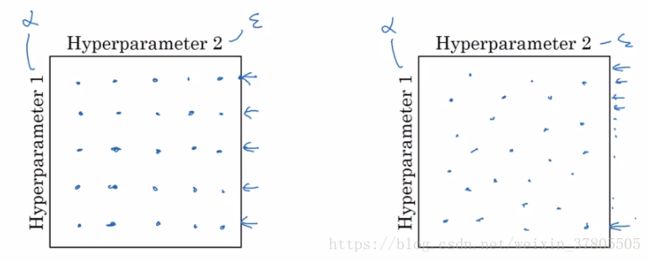
学习速率alpha的设定十分重要。在随机选取时,不要用grid,而是随机选点,如下图,因为可能某个超参数比另一个效果更显著,所以随机选时可以给这个显著参数更多的机会(25个值而非5个值)。
之后可以小范围再进行密度更高的抽样,如下图:
另外,可以选取恰当的scale来研究超参数,比如0.0001-0.1,可以把尺度设为0.0001-0.001,0.001-0.01,0.01-0.1,在每个区域内有相同数量的取样(对数尺度上取样)。这是因为,在小范围内,算法对参数取值的改变可能会更加敏感。
超参数调整方法 1.babysitting a model 2.training many models in parallel,决定条件根据资源够不够。
Batch Normalization
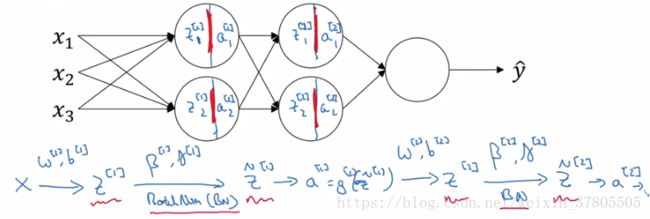
在神经网络中batch norm的使用是对z的操作(它应用于隐藏层,而不是输入项):
在编程框架中,它可能仅仅是一行代码,如在tensorflow里:tf.nn.batch-normalization
那么为什么要批量归一化呢?
协变量:如果我们学习了某种x-y映射,x分布变了,那么就要重新训练算法,尽管x-y映射的真函数没变。比如训练时使用黑猫,测试集用彩色猫,效果就不会好。
批量归一化可以使得:当神经网络在刷新前几层参数时,z21和z22的值会变化,但均值和方差会保持不变。
对神经网络的某一层来讲,这意味着:这一层适应前面层变化的力量被减弱)(因为它们被同一均值和方差限制),有一点独立于其他层的意思,将有效提升整个网络的学习速度。
BN的第二个效果:轻微的正则化。这是因为,归一化后减去均值仍有附加噪声。(使后续的隐藏单元不要过度依赖前面的隐藏单元)在隐藏单元上增加噪声可以解决过拟合问题,即起到正则化的效果。(但不要把BN当做正则化方法)
那么在测试集中,如果只测试一个实例,使用它的均值和方差就不太合理了,要怎么做呢?
当在进行训练时,平均数和方差实际上是用最小批的指数加权平均来计算的,用不同的最小批来训练神经网络时,保持一个移动均值来记录每一层的平均数和方差。最后在测试时,使用当前的z(非z_norm)和训练最新的平均数和方差。
Multi-class classification
softmax回归的一个例子:设猫为class 1,狗 class 2,小鸡 class 3,others class 0
这种情况下,输出层L的单元数为4,最后可以得到四种结果的概率。这时,各类分类的边界是线性的,如下:
softmax来自于和hardmax的对比:同一组数据的结果,softmax可能是[0.842 0.042 0.002 0.114]而hardmax为[1 0 0 0]
Tensorflow
import numpy
import tensorflow as tf
w=tf.Variable(0,dtype=tf.float32)
#cost=tf.add(tf.add(w**2,tf.multiply(-10.,w)),25)
cost=w**2-10*w+25
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost)init=tf.global_variables_initializer()
session=tf.Session()
session.run(init)
print(session.run(w))#输出为0.0session.run(train)
print(session.run(w))#输出为0.1,一次迭代for i in range(1000):
session.run(train)
print(session.run(w))#输出为4.999,接近答案5(1000次迭代)另一种输出相同的写法:
coefficients = np.array([[1.],[-20.],[100.]])
w=tf.Variable(0,dtype=tf.float32)
x=tf.placeholder(tf.float32,[3,1])
#cost=tf.add(tf.add(w**2,tf.multiply(-10.,w)),25)
#cost=w**2-10*w+25
cost=x[0][0]*w**2+x[1][0]*w+x[2][0]session.run(train,feed_dict={x:coefficients})
print(session.run(w))#输出为0.1,一次迭代