数字图像处理及matlab实现知识点总结1-4
第一章概述
图像概念：
图：是物体透射或反射光的分布，客观存在
像：是人的视觉系统对图的接受在大脑中形成的印象或反映。
图像：是图和像的有机结合，是客观世界能量或状态以可视化形式在二维平面上的投影。 
图像处理的目的：
1）提高图像的视觉质量，达到赏心悦目的效果。
2）提高图像中所包含的某些特征或特殊信息，便于计算机分析
3）对图像数据进行交换、编码和压缩，便于图像的存储和传输。
数字图像处理的特点：
1）处理的数据量很大
2）处理占用的频带较宽。
3）各个像素的相关性大
4）不仅能完成线性计算，还能实现非线性计算，具有很高的灵活性。
数字图像处理与模拟图像处理相比的优点：
数字图像比模拟图像的优点：
数字图像不会因图像的存储、传输或复制等一系列操作二导致图像质量的退化，具有很好的再现性，主要优点是：精度高，再现性好，通用性、灵活性强。
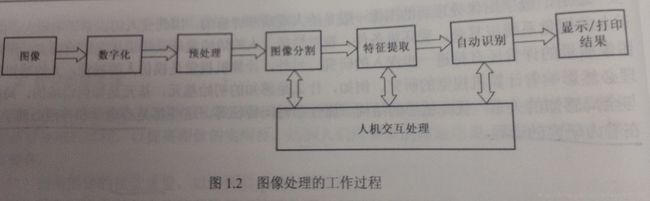
数字图像处理系统结构：
- 图像数字化设备：扫描仪、数码相机、摄像机、图像采集器。
- 图像处理计算机：核心：图像处理计算机；附属：外储存器（硬盘、移动硬盘、光盘、闪盘的核心）
- 图像输出设备：打印机、显示器
具体描述：
数字图像处理主要研究的内容
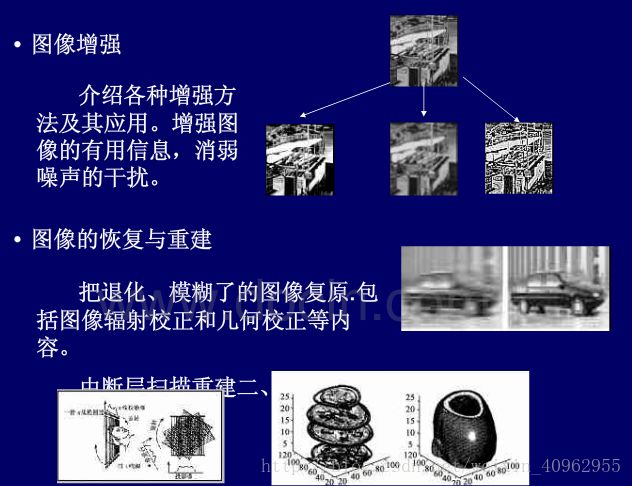
1）图像增强：突出图像中人所感兴趣的部分
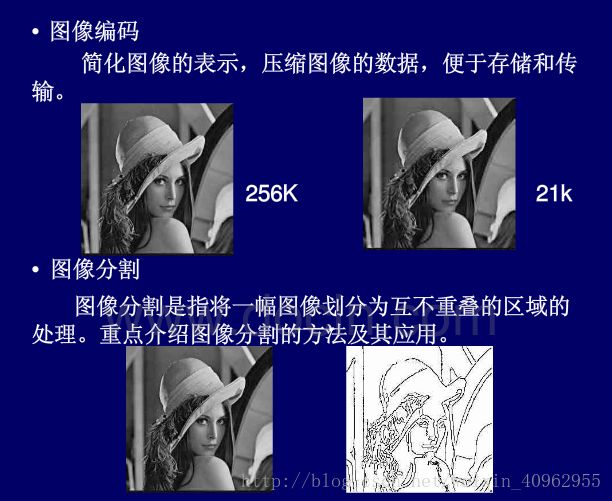
2）图像编码：1.减少数据存储量；2.降低数据率以减少传输宽带；3.压缩信息量，便于特征提取，为后续识别做好准备
3）图像复原：回复图像原貌
4）图像分割：按图像灰度或集合特性分割成若干区域的过程
5）图像分类：在图像经过预处理和特征分割、特征提取后，把不同类别的目标区分开来的图像处理方法。
6）图像重建：从数据到图像的处理过程。（例如CT）
数字图像处理的应用和发展
应用方面
1）航天和航空技术方面（图像复原、特征提取等）
2）生物医学工程方面（CT等）
3）通信工程方面（编码压缩）
4）工业和工程方面（图像识别）
5）军事、公安方面（图像分析、图像复原、图像识别等）
6）文化艺术方面
7）其他
发展
1）图像处理向着高速率、高分辨率、立体化、多媒体化、智能化、标准化发展
2）三维成像和多维成像
3）固化芯片更广阔的应用
4）算法的丰富和深入
第二章 数字图像处理基础
眼视觉系统
人的视觉过程：
1）光学过程：当人眼接收到光刺激时，首先是条件反射
2）化学过程：由视网膜神经进行处理，随后图像信号通过视觉通道反映到大脑皮层
3）神经处理过程：大脑皮层做出相应的处理;存储图像,信息处理、特征提取、决策和描述，最终做出反应。
马赫带效应：
是人类的视觉系统造成的，生物学对马赫带的解释是：人类的视觉系统有增强边缘对比度的机制。
图像的基本知识
1.图像的获取：
图像数字化：
将一幅圆面转化成计算机能处理的形式—数字图像的过程。具体说来，就是把一幅图画分割成一个个小区域(像元或像素)，并将各小区域灰度用整数来表示，形成一幅点阵式的数字图像。它包括采样和量化两个过程。像素的位置和灰度就是像素的属性。
- 1）采样：
将空间上连续的图像变换成离散点的操作称为采样。采砂间隔和采样孔径的大小是内个很重要的参数。采样方式:有缝、无缝和重迭
- 2）量化
经采样图像被分割成空间上离散的像素，但其灰度是连续的，还不能用计算机进行处理。将像素灰度转换成离散的整数值的过程叫量化。
采样量化原则：
1）对于缓变，应细量化，粗采样，以避免假轮廓
2）对于细节丰富的图像，应细采样，粗量化，以避免模糊（混叠）
量化等级越多，所得图像层次越丰富，灰度分辨率高，图像质量好，但数据量大;量化等级越少，图像层次欠丰富，灰度分辨率低，会出现假轮廓现象，图像质量变差，但数据量小。
但在极少数情况下对固定图像大小时，减少灰度级能改善质量，产生这种情况的最可能原因是减少灰度级一般会增加图像的对比度。例如 ：对细节比较丰富的图像数字化。
2.像素间的基本关系
1.邻接关系
N4（p）:（x+1,y）,（x-1,y）,（x,y-1）,（x,y+1）;
ND（p）:（x+1,y+1）,（x-1,y-1）,（x-1,y+1）,（x+1,y-1）.
4邻域 N4（p）
8邻域 N8（p） : N4（p）+ND（p）
4邻接：q在N4（p）中，具有v的两个像素 p, q 是4邻接。
8邻接：q在N8（p）中，具有v的两个像素 p, q 是8邻接。
m邻接: 1) q在N4（p）中，或者2) q在ND（p）中且集合N4（p）和N4（q）交集没有v值的像素，则具有v的两个像素 p, q 是m邻接.
- 1）4邻接必8邻接，反之不然
- 2）m邻接必8邻接，反之不然
- 3）m邻接是8邻接的变型，介于4邻接和8邻接之间，以消除8邻接中产生的歧义性。
- *像素间同时存在4邻接和8邻接是优先4邻接。
2.距离
图像分类
1）二值图像：图像的每个像素只能是黑或白，没有巾间的过渡，二值图像的像素值为0或1。
2）亮度图像：像素灰度值用8Bit表示，介于黑白之间的256种灰度中的一种。
3）索引图：颜色是预先定义好的，有256种颜色通过索引来表示，每个像素占8bit
4）RGB图像：真彩色图像，每个像素由红蓝绿三个字节组合而成，可产生1670万种不同颜色。
10.什么是图像灰度直方图? 图像直方图反映了图像的什么特征?
灰度的直方图反映图像中灰度级与出现这种灰度的概率之间关系的图形。这种图形能够反映图像灰度级的分布统计特征。
第三章图像基本运算
1.点运算
1）线性点运算
S=ar+b
a=1,b=0,不变
a=1,b#0,灰度值上移或下移，图像变亮或暗
a>1,对比度变大
a<1,对比度降低
a<0,暗区变亮，亮区变暗。
2）非线性点运算
一般式：
S=c∗log（1+r）
c为常数，r>=0.
幂变式（imadjust）：
S=c∗ry
y>1,高灰度的对比度增强
y<1,低灰度的对比度增强
y=1，不改变图像
2.代数运算
- 加（addition）
平均值去噪：
Di（x,y）=Si（x,y）+Ni（x,y）
S为理想图，N为噪音。
信噪比：P（x,y）=S2（x,y）/E[N2（x,y）]
对图做平均为：
平均D（x,y）=1/M∗sum（S（x,y）+Ni（x,y））
对应信噪比：P（x,y）=S2（x,y）/E[1/M∗sum（Ni（x,y））]2
使得信噪比增加M倍。
减（Subtration）：
检测变化及运动的物体乘（Multiplication）：
改变图像的灰度值，实现灰度级变换。除（Division）：
改变图像的灰度值（比值图像处理）
3.逻辑运算
AND,OR,NOT
4.几何运算
- 平移
x1=x0+（−）X;y1=y0+（−）Y
x（i,j）=I（i-a,j-b）#左右平移 - 镜像
【M，N】=size（I）
x（i,j）=I（i,N-j+1）#左右水平镜像
x（i,j）=I（M-i+1,j）#上下水平镜像 - 旋转（imrotate）
1) J=（I，60，’bilinear’）
2) J=（I，60，’bilinear’,’crop’）#截去局部 - 缩放
插值方法
1）最近邻插值法：缩小（取原图的偶数行，或取奇数行）；
2）插值算法
灰度重采样：
- 最近邻法（nearest）：取最近点的灰度值为点的灰度值
- 双线性插值法（bilinear）：考虑周围4个邻点的灰度值对它的影响。
f（u0,v0）=[f（u+1,v）−f（u,v）]∗a+[f（u,v+1）−f（u,v）]∗b
+[f（u+1,v+1）+f（u,v）−f（u,v+1）−f（u+1,v）]∗a∗b+f（u,v）
- 三次内插法（bicubic）：考虑周围16个邻点的灰度值对它的影响。
第四章图像转换
1.图像变换的目的:
- ①图像处理问题简化;
- ②有利于图像特征提取;
- ③有助于从概念上增强对图像信息的理解。
2.图像变换的要求
图像变换通常是一种二维正交变换。一般要求:
①正交变换必须是可逆的;
②正变换和反变换的算法不能太复杂;
③正交变换的特点是在变换域中图像能量将集中分布在低频率成分上，边缘、线状信息反映在高频率成分上，有利于图像处理。因此正交变换广泛应用在图像增强、图像恢复、特征提取、图像压缩编码和形状分析等方而。
3.傅立叶变换
3.1一维二维连续函数的傅立叶变换
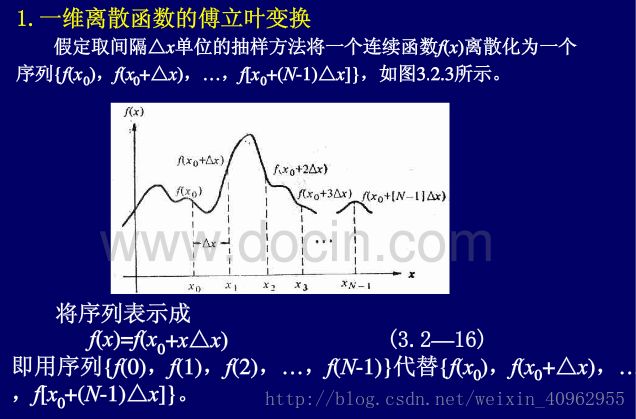
3.2一维二维离散函数的傅立叶变换
4.二维离散傅立叶变换的若干性质
离散傅立叶变换建立了函数在空间域与频率域之间的转换关系。在数字图像处理中，经常要利用这种转换关系及其转换规律，因此，下而将介绍离散傅立叶变换的若下承要性质。
(1)周期性和共扼对称性
若离散的傅立叶变换和它的反变换周期为N，则有
F(u,v)=F(u+N，v)=F(u+，v+N)=F(u+N,v+N)
傅立叶变换存在共扼对称性F(u,v)=F′(−u,−v)这种周期性和共扼对称性对图像的频谱分析和显示带来很大益处。
(2)分离性
一个二维傅立叶变换可由连续两次一维傅立叶变换来实现
(3)旋转性质
平面直角坐标写成极坐标形式.
5.卷积定理
f（u）∗g（u）=F（u）∗G（u）