120三角形最小路径和——力扣算法系列2020.07.14 Python
第20天
2020.07.14 周二
难度系数：中等
题目：120三角形最小路径和
给定一个三角形，找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。
例如，给定三角形：
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。
说明：
如果你可以只使用 O(n) 的额外空间（n 为三角形的总行数）来解决这个问题，那么你的算法会很加分。
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/triangle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。
——————————我是分割线——————————
解法：
思路：动态规划
n行（len(triangle)）
第i行（i从0开始）有i+1个元素
把每行的左端对齐，则形成一个直角三角形
从(0,0)走到(i,j)，且每次只能向下或者右下走一步。即要走到(i,j)则上一步必须为(i-1,j-1)或者(i-1,j)
2
3，4
6，5，7
4，1，8，3
状态定义：dp[i][j]:从三角形顶部走到(i,j)的最小路径和
状态转移：dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) +triangle[i][j]
特别注意，第i行有i+1个元素，j的取值范围是0到i。当j=0或j=i时，状态转移方程中有一些无意义的项。
每行的最左侧元素dp[i][0] = dp[i-1][0] + triangle[i][0]
每行的最右侧元素dp[i][i] = dp[i-1][i-1] + triangle[i][i]
边界条件：dp[0][0] = triangle[0][0]三角形顶部
从1到n遍历枚举i
从0到i遍历枚举j
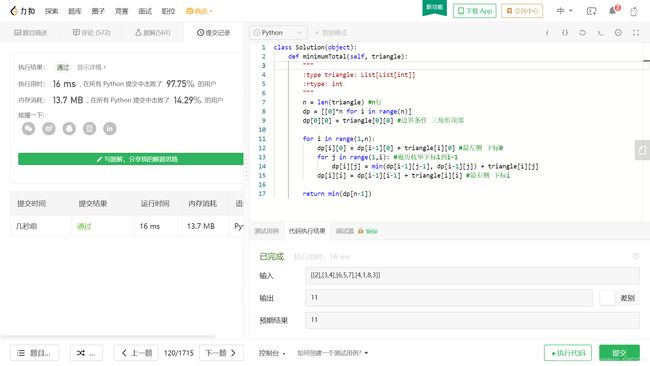
代码：
# leetcode120三角形最小路径和 2020.07.14
class Solution(object):
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
n = len(triangle) #n行
dp = [[0]*n for i in range(n)]
dp[0][0] = triangle[0][0] #边界条件 三角形顶部
for i in range(1,n):
dp[i][0] = dp[i-1][0] + triangle[i][0] #最左侧 下标0
for j in range(1,i): #遍历枚举下标1到i-1
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]
dp[i][i] = dp[i-1][i-1] + triangle[i][i] #最右侧 下标i
return min(dp[n-1])
triangle = [
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
print(Solution().minimumTotal(triangle))
# 结果11
时间复杂度：O(n²) n是三角形的行数
空间复杂度：O(n²) 需要一个n*n的二维数组来存放所有的状态