支持向量机SVM

注：本文节选自《 精通数据科学：从线性回归到深度学习》一书，如有侵权，请联系删除。
联系邮箱：[email protected]

1. 支持向量学习机

支持向量学习机（Support Vector Machine，SVM）是一款非常强大的分类模型。它曾经是最好的（不少人相信它现在仍是最好的）监督式机器学习模型，甚至被称为“万能分类器”。在数学上，支持向量学习机的模型处理较为复杂，涉及的知识也较为深奥，常常让人觉得难以理解。因此，本节先略过这些难以理解的数学推导，从直观上和实际操作上来讨论这个模型。
与讨论逻辑回归模型不同，本节只讨论如何用支持向量学习机模型解决二元分类问题。对于多元分类问题，支持向量学习机常使用one-vs.-all策略将其拆分为多个二元分类问题解决。

1.1 直观例子

先来看一个简单的例子。假设面对的二元分类问题有两个自变量，分别为$x_1$和$x_2$。将数据集里的数据表现在图上，可以得到图1，其中圆点表示类别1，三角形表示类别0。

图1

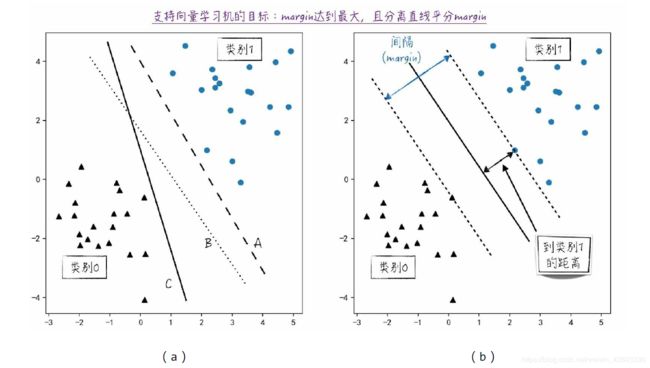
从图像上来看，这两个类别能够被一条直线完美地分开，比如图1(a)中的A、B、C三条直线。这样的数据在学术上被称为线性可分（linearly separable），而分开它们的直线叫作分离超平面（separating hyperplane）。

如果将直线A上方的数据预测为类别1，直线A下方的数据预测为类别0，可以得到一个百分之百准确的分类模型。对直线B、C结论也同样成立。那么，哪一条直线代表的是更加完美的模型呢？从直观上来讲，直线B所代表的模型更好，因为它跟每个数据点都离得比较远，而且离两个类别的距离大致相同。换句话说，直线B的倾斜度更加合理，而且位置更加“居中”。相比之下，其他两条直线的倾斜度显得不太合理，而且直线A与类别1贴得太近，直线C又距离类别0太近。

除了图图1(a)中画出的A、B、C三条直线外，其实还存在着无数条直线可以将不同类别的数据完全分开。为了从中选出最优的直线，需要将上面提到的倾斜度和位置“居中”做更加量化的解释。

在解决这个问题之前，先来看看数据点到分离直线的距离代表了什么。从之前的讨论可知，作为分离超平面的直线其实是解决分类问题的标准线。落在它上方的点被归为一类，落在它下方的点被归为另一类。那么极端一些，如果某个数据点刚好落在直线上，那么它被归为任何一类都是同样有道理的。因此在支持向量学习机模型里，一个数据点离分离直线的距离代表了模型对这一点预测结果的“自信程度”（在学术上称为置信度），离得越近，模型对预测结果越没有把握。 这个结论其实有比较严谨的数学依据，具体的细节将在下节中详细讨论。

基于上面对距离（点到直线）的讨论，支持向量学习机会按照如下的两个原则寻找最优的分离直线。

• 对于一条分离直线，定义它到某一类别的距离等于这个类别中的所有点到这条直线距离的最小值。比如对于图1(b)中的实线，虚线（它与实线平行）经过的圆点到实线的距离就是分离直线到类别1的距离。支持向量学习机想要最大化分离直线到两个类别的距离之和，在学术上称之为间隔（margin），如图1(b)所示。值得注意的是，一旦分离直线的倾斜度确定了，间隔其实也就确定了。因此，最大化间隔这个目标就确定分离直线的倾斜度。
• 在默认情况下，所有数据点的权重都是一样的。所以分离直线到每个类别的距离应该相等。因此如图1(b)所示，分离直线应该在两条平行虚线的中间，这样就确定了分离直线的位置。

1.2 用数学理解直观

本节的任务是将上面讨论的直观原则转换为严谨的数学定义。在开始这项艰巨的任务之前，先来简单回顾一下有关线性几何的基础知识，这些数学知识是理解后面讨论的关键。需要注意的是，在支持向量学习机的数学讨论中，我们将大量使用向量的内积运算（dot production）。这与前面章节讨论过的线性回归和逻辑回归有所不同，这两个模型的数学推导主要使用向量的矩阵乘法。在数学上，矩阵乘法与欧式空间内的向量内积在本质上是一样的，也可以互相推导。前面章节使用矩阵乘法来推导模型，是为了和学术主流表达方式保持一致，以免读者在阅读其他相关文献时，由于数学符号的不同而感到不解。

先从最直观的二维线性空间谈起，如图2所示。

​ 图2

对于二维空间中的一条直线，假设原点到这条直线的投影为向量$\beta$，也就是说向量$\beta$与直线垂直。那么，对于直线上的任意一点$T$，向量$T-\beta$与向量$\beta$的内积等于0。因此，直线可以用一个线性方程来表示，具体的公式如下：

​ $$\beta \cdot (T-\beta )=0$$ （1-1）

反过来，对于任意一个二元线性函数，不妨设为$f(X)=\gamma \cdot X$，则二元线性方程$f(X)=0$在空间中表示一条直线。事实上，假设点$X_0$使得$f(X_0)=0$，对于满足$f(X)=0$的任意一点，公式（1-2）成立。

​ $$\gamma \cdot (X-X_0)=0-0=0$$ （1-2）

也就是说，向量$X-X_0$ 与向量$\gamma$ 垂直，这表明所有的点都在同一条直线上。而且显然这条直线上的所有点也都满足$f(X)=0$，所以任意一个二元线性方程在空间中表示一条直线。

现在再次回到直线，为了表示简单，不妨设它的代数表示为公式（1-1）。那么空间中的任意一点到这条直线的垂直距离应该如何表示呢？分两种情况来讨论，如图2所示。

• 如果点在直线上方，比如$X_1$，假设它到直线的距离为$\mid \mid k\mid \mid$，那么根据内积的定义，可以得到：
  $$\beta \cdot (X_1-\beta )=\mid \mid \beta \mid \mid \mid \mid k\mid \mid cos0=\mid \mid \beta \mid \mid \mid \mid k\mid \mid$$ (1-3)

• 如果点在直线下方，比如$X_2$，假设它到直线的距离为$\mid \mid l\mid \mid$，那么类似地可以得到：

​ $$\beta \cdot (X_2-\beta )=\mid \mid \beta \mid \mid \mid \mid l\mid \mid cos\pi =-\mid \mid \beta \mid \mid \mid \mid l\mid \mid$$ (1-4)

将上面的讨论总结一下，对于一个给定的线性方程$f(X)=\gamma \cdot X$，绝对值$\mid f(X)\mid$与点$X$到直线 $f(X)=0$ 的距离成正比，而$f(X)$的符号表示点到直线的垂线方向。这个结论不仅仅针对二维空间，在高维空间同样成立。只不过在高维空间里，直线要变成超平面。

有了上面的代数知识，让我们稍稍离题一下，再次讨论逻辑回归模型。逻辑回归模型同样也是一个分类模型，不妨设模型所用的自变量为$X$，需要预测的因变量为$Y$，其中，$Y=1$ 表示一类， $Y=0$表示另一类，则它的预测公式如下：

​ $$P(Y=1)=1/(1+e^{-X\beta })$$ (1-5)

公式（2-5）中的线性部分记为函数$f(X)=X\cdot \beta$，当$f(X)>0$时，$f(X)$ 越大，模型预测的概率就越接近于1。根据上面的讨论可以知道，当$f(X)>0$时，$f(X)$与$X$到超平面$f(X)=0$的距离成正比。这用几何直观的语言表示出来就是：**若一个点在超平面正向一侧，它离超平面越远，逻辑回归模型就越有把握预测它的标签等于1。**类似地，可以得到当$f(X)<0$时的几何直观解释：若一个点在超平面反向一侧，它离超平面越远，逻辑回归模型就越有把握预测它的标签等于0。
将上述内容总结一下，从几何直观上，逻辑回归模型的分类原理可描述为：模型的线性部分$X\beta =0$定义了分类的分离超平面，离这个超平面越远，模型对相应的预测结果把握越大。而这与第1节中讨论的支持向量学习机的分类思路非常相近。因此，支持向量学习机可以被看作逻辑回归的一种“基因突变”。虽然两者外表看起来相差很大，但其数学本质在很大程度上是一致的。

1.3 从几何直观到最优化问题

现在回来看在数据线性可分的情况下，用数学语言描述支持向量学习机模型，或者讲得直接一些，我们将找出这个模型对应的最优化问题。在下面的讨论中，假设训练数据$i$的自变量为$X_i$，被预测量为$y_i$。

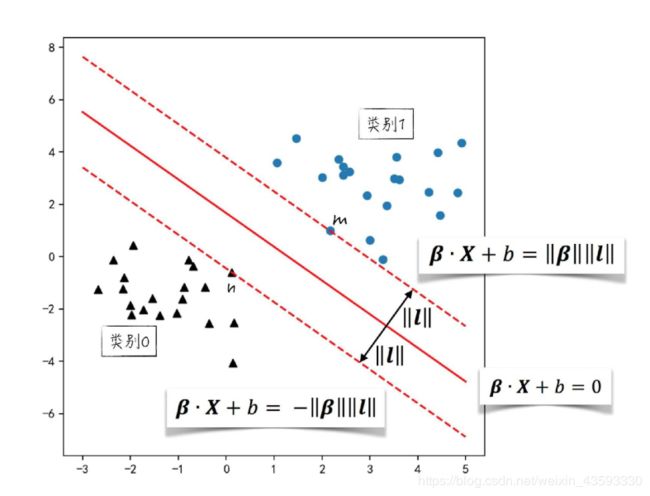
如图3所示，分离直线记为$\beta \cdot X+b=0$，而虚线穿过的点分别表示两者类别中到分离直线最近的点，记为点$m$和点$n$。根据模型分类的第二点原则，直线是居中的，因此$m$和$n$到分离直线的距离都为$\mid \mid l\mid \mid$。

​ 图3

同公式（1-3）和公式（1-4）类似，图2-3中的两边虚线分别可以表示为$\beta \cdot X+b=\mid \mid \beta \mid \mid \mid \mid l\mid \mid$ 和 $\beta \cdot X+b=-\mid \mid \beta \mid \mid \mid \mid l\mid \mid$。

对于类别1中的任意一点$X_i$，它到分离直线的距离大于$\mid \mid l\mid \mid$ ，因此， $\beta \cdot X_i+b>\mid \mid \beta \mid \mid \mid \mid l\mid \mid$。类似地，对于类别0中的任意一点$X_i$，它到分离直线的距离也大于$\mid \mid l\mid \mid$ ，而且它在直线的下方，因此， $\beta \cdot X_i+b<-\mid \mid \beta \mid \mid \mid \mid l\mid \mid$。

支持向量学习机的目的是最大化两条虚线之间的距离（也就是之前提到的margin）。那么模型的最优化问题可以表示为公式（1-6）。

​ $$max2\mid \mid l\mid \mid$$

​ 任一$X$属于类别1， $$\beta \cdot X+b\ge \mid \mid \beta \mid \mid \mid \mid l\mid \mid$$

​ 任一$X$属于类别0，$$\beta \cdot X+b\le -\mid \mid \beta \mid \mid \mid \mid l\mid \mid$$ (1-6)

为了后面的计算更加方便，记$w=\beta /\mid \mid l\mid \mid \mid \mid \beta \mid \mid$，$c=b/\mid \mid l\mid \mid \mid \mid \beta \mid \mid$可以得到。因此将公式（1-6）改写为更为标准的公式（1-7）。之后的讨论都将基于后者。

​ $$max\frac{2}{\mid \mid w\mid \mid }$$

​ 任一$X$属于类别1， $$w\cdot X+c\ge 1$$

​ 任一$X$属于类别0， $$w\cdot X+c\le -1$$ (1-7)

同时，我们用$y_i=1$表示类别1， $y_i=-1$表示类别0。那么在公式（1-7）中的限制条件两边同时乘以$y_i $，可以将两条限制条件合并为一条。同时注意到， $max\frac{2}{\mid \mid w\mid \mid }$ 等价于$min\frac{1}{2}{\mid \mid w\mid \mid }^2$。这样就得到了支持向量学习机最简洁也是最常用的数学表示（在数据线性可分的情况下）。

​ $$min\frac{1}{2}{\mid \mid w\mid \mid }^2$$

​ $$y_i(w\cdot X_i+c)\ge 1$$ (1-8)

求解公式（1-8）所描述的最优化问题，就可以得到支持向量学习机模型参数的估计值，不妨设为$\hat{w}$，$\hat{c}$。模型的预测公式如下，其中，$\widehat{y_i}$ 表示模型的预测结果，而$sign$表示数字的符号，当$x>0$时，$sign(x)=1$ ；否则$sign(x)=-1$。

​ $$\widehat{y_i}=sign(\hat{w}\cdot X_i+\hat{c})$$ (1-9)

值得注意的是， 公式（ 1-8） 是带有限制条件的最优化问题（ 限制条件为 $y_i(w\cdot X_i+c)\ge 1$ ） 。 这和之前接触到线性回归和逻辑回归不同， 它们对应的最优化问题是没有限制条件的， 比如针对线性回归模型， 参数估算公式为$\hat{\beta }=argmin{\sum }_i(y_i-X_i\beta {)}^2$。
在数学上， 求解有限制条件的最优化问题比没有限制条件的更加困难， 所用的数学工具也有所差异。

1.4 损失项

到目前为止， 我们都在数据线性可分的情况下， 讨论支持向量学习机的分类方法。 但如果仅限于此， 支持向量学习机这个模型几乎没有实用价值。 因为在现实生活中， 需要处理的数据集绝大多数都是线性不可分的， 也就是说不存在一个超平面使得不同类别的数据分别落在平面的不同两侧。 以图4为例， 图中的点$a$是类别0，但它更靠近类别1的中心。 针对这份数据， 就没有办法像之前一样， 用一条直线将两个类别完全分开。 那在这种情况下， 支持向量学习机会如何处理呢？ 答案就是加入损失项。

​ 图4

在数学上， 支持向量学习机通过公式（1-8）中的条件 $y_i(w\cdot X_i+c)\ge 1$ 来保证分类结果的准确。 比如在图4中， 这个条件将保证数据表示的点都落在两条虚线的外面， 这也是模型的分类假设。 现在由于数据线性不可分， 所以将这个条件稍稍放松一点， 改为 $y_i(w\cdot X_i+c)\ge 1-{\xi }_i$。 其中 ${\xi }_i>0$ ， 它与点$i$离相应虚线的距离成正比。比如图4中点$a$ ， 可以计算得到它到下方虚线的距离为${\xi }_a/\mid \mid w\mid \mid$ ， 到分离超平面（ 实线） 的距离为 $({\xi }_a-1)/\mid \mid w\mid \mid$。 需要注意的是， 这里计算的距离是空间的实际欧式距离。 但在机器学习中（ 比如第三方模型库scikit-learn） ， 针对一个支持向量学习机模型， 常把函数值${\xi }_a-1=w\cdot X_a+c$ （ 注意到图中的 $a$点有$y_a=-1$ ） 称为数据到分离超平面的“距离” 。

因此， ${\xi }_i$可以被看作模型在数据$i$这一点违反自身分类原则的程度， 也就是模型在这一点的损失。 那么它们的和 ${\sum }_i{\xi }_i$当然是越小越好。 这个目标和模型本身的目标（ 最大化margin） 相矛盾， 比如在图4中， 模型原本的目标是最大化两条虚线之间的距离， 但如果两条虚线离得越远， 显然， 模型“错误” 的损失${\sum }_i{\xi }_i$ 也越大。也就是说， 从数学上来看函数 $\frac{1}{2}{\mid \mid w\mid \mid }^2$ 和函数${\sum }_i{\xi }_i$ 是负相关关系， 就像跷跷板的两头一样。

为了兼顾上面提到的两个模型目标， 我们通过线性函数来折中。 具体地， 支持向量学习机的最优化问题被改为公式（1-10) 。 其中， $C>0$为模型的损失系数， 是一个超参数， 它对模型结果的影响将在后面讨论。

​ $$min\frac{1}{2}{\mid \mid w\mid \mid }^2+C\sum _i{\xi }_i$$

​ $$y_i(w\cdot X_i+c)\ge 1-{\xi }_i;{\xi }_i\ge 0$$ (1-10)

在实际应用中， 不管数据是否线性可分， 都会根据公式（1-10） 来估计支持向量学习机的模型参数。 公式（1-8） 更多地只是为了展示模型的建模思路。

1.5 损失函数与惩罚项

接下来， 我们将支持向量学习机对应的最优化问题（公式（1-10）) 转换为不带限制条件的最优化问题。 首先只考虑目标函数中的损失部分${\sum }_i{\xi }_i$ 。 在不影响其他参数的情况下， ${\xi }_i$越接近于0越好。 由此可以得到 ${\xi }_i$的表达式 :

​ $${\xi }_i=max(0,1-y_i(w\cdot X_i+c))$$ (1-11)

事实上， 公式（ 1-11） 已经包含了公式（ 1-10） 中的限制条件。 理由如下：

​ $${\xi }_i=max(0,1-y_i(w\cdot X_i+c))\ge 1-y_i(w\cdot X_i+c)$$ (1-12)

那么支持向量学习机的参数估计公式可改写为， 其中， $C>0$ 是模型给定的超参数 。

​ $$mi{n}_{w,c}(\frac{1}{2}{\mid \mid w\mid \mid }^2+C\sum _{i}max(0,1-y_i(w\cdot X_i+c)))$$ (1-13)

公式（ 1-13） 其实定义了支持向量学习机的损失函数： $L=\frac{1}{2}{\mid \mid w\mid \mid }^2+C{\sum }_{i}max(0,1-y_i(w\cdot X_i+c))$ ， 将它分为如下两部分。

• 模型的预测损失$LL={\sum }_{i}max(0,1-y_i(w\cdot X_i+c))$ ， 学术上称这个函数为hinge loss。 由此可以看到支持向量学习机的预测损失， 其实是由一个线性损失函数外套一个非线性变换构成的。 这再一次印证了在前面重复过很多次的一个观点： 复杂模型都是由线性模型和非线性变换一层层嵌套构成的。 在支持向量学习机中， 非线性变换部分$f(x)=max(0,x)$ 是所谓的线性整流函数（ReLU） 。 它是深度学习中非常重要的一个函数， 我们将在后面的章节中详细讨论这个函数的细节。

• 惩罚项 $\frac{1}{2}{\mid \mid w\mid \mid }^2$。 为了解决模型过拟合的问题， 讨论了惩罚项这个概念， 而这里的 $\frac{1}{2}{\mid \mid w\mid \mid }^2$ 正是$L2$惩罚项。 虽然在支持向量学习机中， 这一项的初衷是最大化margin， 使得分离超平面尽量远离边缘数据点， 但这样会在分类分界面和数据之间留出一道空隙， 在某种程度上的确防止了模型出现过拟合， 因此符合惩罚项的定义。 与其他模型不同的是， 支持向量学习机的惩罚项是并不可少的， 而其他模型在理论上并没有这样的要求（ 虽然在实际应用中，不管使用什么模型，在损失函数中加入惩罚项几乎是一定的）。

综合上面的分析， 支持向量学习机的场景类型和损失函数如图5所示。

​ 图5

1.6 Hard margin与soft margin比较

在支持向量学习机的损失函数中， 有一个很重要的超参数——模型的损失系数$C$。 这个超参数的取值将极大地影响模型的分类结果。 为了说明这个问题， 再来看看模型的损失函数：

​ $$L=\frac{1}{2}{\mid \mid w\mid \mid }^2+C\sum _{i}max(0,1-y_i(w\cdot X_i+c))$$ （1-14）

超参数 $C$其实是模型预测损失的权重， 它的值很大表示模型将更加在意分类“错误” 而轻视margin的大小。 下面用一个具体的例子来展示这种影响， 具体实现如程序清单1所示。

（ 1）公式（1-14） 所表示的模型其实是线性支持向量学习机（ 非线性支持向量学习机将在后面讨论） 。 对于这种模型， 第三方库scikit-learn提供了两种实现方式： 一种是sklearn.svm.SVC， 如第1行代码所示； 另一种是sklearn.svm.LinearSVC。 虽然使用后一种实现， 可以为线性SVM选择其他种类的损失函数和惩罚项， 但在实际中， 更加常用的是第一种实现（ 因为可以方便地更换核函数） 。

（ 2）类SVC里有参数“C”， 这个参数就是公式（1-14） 里的 。 因此如第11行代码所示， 对同一数据集使用不同的损失系数 $C$训练模型， 然后将这些不同模型的结果可视化。 值得注意的是， SVC里的参数“kernel”表示支持向量学习机所使用的核函数， 这里使用“linear”（ 线性核函数） 。

（ 3）对于训练好的模型“re” ， 它有一个函数：decision_function。 将数据$i$ 的自变量部分（ 即$X_i$） 传给它， 可以得到该数据到分离超平面的“距离” 。 但值得注意的是， 正如前面提到的， 这里所指的“距离” 并非空间中的欧式距离，而是函数值$w\cdot X_i+c$ 。 因此， “decision_function=±1”刚好对应着图6a中的虚线 。

​ 图6

运行完整的代码， 可以得到如图6所示的结果。 从整体上来看， 随着参数$C$的增大， margin width（ 两条虚线之间的距离） 会减小， 如图6b所示。
从分类结果上来看， 当 $C$的取值比较小时， 比如$C=0.1$ ， 有比较多的点落在相应的虚线之间， 甚至有的越过了实线， 换句话说， 模型更注重的是靠近类别中心的数据点。 在学术上， 这种情况被形象地称为soft margin； 当$C$ 的取值比较大时， 比如$C=10000$， 几乎没有点落在相应的虚线之间， 也就是说， 模型对靠近分离超平面的“异常点” 更加重视。 类似地， 这种情况在学术上被称为hard margin， 如图6a所示。

在实际应用中， 参数$C$ 可以被当作模型的超参数来使用： 通过网点搜寻（ grid search） 来找到使预测效果最好的取值。 也可以根据实际需要， 人为地选择合适的值， 比如对于搭建模型的数据， 如果已知其中有比较多的随机扰动， 那么就应该选择较小的$C$ 值， 也就是soft margin， 使模型结果少受数据噪声的影响。

1.7 支持向量学习机与逻辑回归： 隐藏的假设

支持向量学习机和逻辑回归都是分类模型， 那么这两个模型有什么不同呢？ 在实际应用中， 针对一个具体的问题， 应该如何选择它们呢？ 我们先通过一个简单的例子来看这两个模型的差异。
（1） 首先生成一批较少的， 离得比较近的数据集。 如图7a所示， 数据分为两个类别， 图形符号与之前的例子保持一致。 对这批数据分别使用支持向量学习机和逻辑回归建模， 并将得到的模型结果也表现在图上。 其中实线表示支持向量学习机的分离超平面， 点线表示逻辑回归的分离超平面。

（2） 在第（1）步数据集的基础上， 增加一批数量比较多， 离得比较远的新数据， 如图7b所示。 两幅图中用方框圈起来的数据是一样的。 针对这个新的数据集， 同样分别使用两种模型建模， 并将相应结果表现在图上。

​ 图7

对比图7a和图7b中的实线会发现虽然训练模型的数据是不一样的， 但支持向量学习机（ 模型的损失系数$C=1$ ） 的模型结果是一模一样的。 换句话说， 新加入的数据对模型结果没有影响。 从数据的角度来讲， 由于新加入的数据远离分离超平面， 所以它们在支持向量学习机这个模型里的权重等于0。 这正是支持向量学习机的隐含假设： 每个数据点权重其实并不一样， 越靠近分离超平面， 数据的权重也就越大。 而且损失系数$C$ 越大（hard margin），数据权重不一样的现象也就越严重， 如图8所示， hard margin在两组数据里的模型结果是一样的， 而soft margin的结果则有较大变化。 支持向量学习机的这个隐含假设其实有严谨的数学证明。

​ 图8

对这种模型隐含假设的理解是至关重要的。 毫不夸张地说， 这是区分优秀数据科学家的标准之一。 这种隐含假设与模型的其他假设不同， 在搭建模型时并没有被明确地提出， 所以往往被大家忽略， 但它们对模型结果的影响又是巨大的。 建模时， 如果忽略或者没能正确地处理这种假设， 会导致模型结果较差甚至完全错误，而且会让人产生错误的幻觉： 数据满足模型的每一个假设， 但模型的效果就是不好。
而逻辑回归则没有这样的隐含假设， 除非特殊处理， 模型对每个数据点的权重都是一样的。 因此当加入新数据后， 模型的结果发生了比较大的改变， 如图7a和图7b中的点线所示。
总结一下， 这两个模型对数据权重的隐含假设并不相同。 这也给了我们选择模型的一个依据， 如果希望模型对数据中靠近“边缘” 的点更加敏感， 则推荐使用hard margin支持向量学习机。 如果需要综合考虑每一个点， 则需要使用逻辑回归或者soft margin支持向量学习机。

2. 核函数

核函数（ kernel function或者kernel trick） 是机器学习中十分重要的数据处理技巧。 通过核函数， 我们可以将原空间中非线性的数据映射为高维或无限维空间中近似线性关系的数据。 既然在新的空间里， 数据是近似线性关系， 那么就可以使用线性模型对其建模分析。 这和本书一直强调的建模思路是一致的： 通过某种数学变换， 将非线性问题转换为线性问题解决。

在实际生产中， 核函数常常结合支持向量学习机一起使用， 使得模型能够解决各类非线性分类问题。 当然， 几乎所有的机器学习模型都可以搭配核函数使用， 比如线性回归模型加上核函数得到所谓的核岭回归（Kernel Ridge Regression，KRR） 。 虽然机器学习的模型繁多， 差异很大， 但它们搭配核函数的方法大体上是一致的， 因此本节以支持向量学习机为例， 讨论核函数的使用 。

2.1 空间变换：从非线性到线性

在第1节中， 我们讨论了经典的支持向量学习机。 它也被称为线性支持向量学习机， 因为它建模的思路就是用一个线性的分离超平面去解决数据的分类问题。 虽然对于线性不可分的数据， 1.4节提供了所谓的soft margin解决方案， 但这种方法只是部分（ 很少的一部分） 解决了非线性数据的分类问题。 对于绝大部分的非线性分类问题， 它是无法很好解决的。 以二维空间为例， 从直观上来讲， soft margin的模型结果依然是一条直线。 那如果数据本身就是按一条曲线来区分类别的呢？ 在这种情况下， 数据不再满足soft margin的模型假设， 因此最后的模型效果一定不好。

用一个具体的例子来展现上面描述的问题。 如图9a所示， 沿用之前的表示方式， 圆点表示类别1， 三角形表示类别0。 直观上， 对于图中表示的数据， 无论怎么画直线， 都没有办法将两种类别的数据很好地分开， 因为类别1的数据好像被类别0的数据紧紧地“包围” 住。 事实上如果对这批数据使用线性支持向量学习机模型，得到的结果就是所有数据都被预测为类别0。

​ 图9

但如果换个角度， 在图中画一个以原点为中心，半径为1的圆圈， 则刚好可以很完美地将两个类别的数据分开， 如图9a所示， 三角形全部落在圆圈外的灰色区域。 这么看来， 为了解决这个问题， 需要重新设计一款“圆圈版” 的支持向量学习机， 但事情并没有想象中那么复杂。 从空间变换的角度重新梳理一下“画圆圈” 这件事情， 假设图9a的横纵坐标为$x_1,x_2$ ， 如图9b所示， 将坐标系的横坐标改为$x_1^2$、 纵坐标改为 。$x_2^2$ 那么图9a中的圆圈就变成了图9b中的直线， 而圆圈内的圆点会落在新坐标系下的左下角三角区域内。 这样， 原本非线性的分类问题在新的坐标系下就变成了线性的分类问题， 而后者可以用支持向量学习机完美地解决。 将上面的整个过程抽象为严格的数学语言 。

• 假设分类问题的原始数据为$\{X_i,y_i\}$ ， 其中，$X_i$为自变量，$y_i$ 为被预测量。

• 找到一个非线性的空间变换$\varphi$ ， 将数据转换为$\{\varphi (X_i),y_i\}$ 。 比如上面的例子中，$X_i=(x_{1,i},x_{2,i})$、$\varphi (X_i)=X_i=(x_{1,i}^2,x_{2,i}^2)$。

• 使用转换后的新数据训练模型， 并得到如下的预测公式， 它与公式（18-9）（ 线性支持向量学习机的预测公式） 非常相似 。

  ​ $$\widehat{y_i}=sign(\hat{w}\cdot \varphi (X_i)+\hat{c})$$ （2-1）

这个方法在理论上很完美， 但实际上很难直接使用， 原因主要有两个。 首先，很难得到转换函数$\varphi$的具体表达式。 在上面的例子中， 数据只是二维的， 我们通过将其可视化才联想到相应的转换函数。 在实际产生中， 数据是高维的， 很难将其可视化。 即使能将数据直观地呈现出来， 也很难从中联想到要如何做高维空间之间的变换。 其次， 对于非线性分类问题， 往往要将原始数据转换到高维空间才能达到近似线性可分的目的（ 这其实相当于从原始数据中提取更多特征来搭建模型） 。 因此，如果直接使用$\{\varphi (X_i),y_i\}$ 训练模型， 则常常导致模型的运算复杂度过高， 工程上几乎无法实现。

这两个难题可以被核函数很好地解决。 核函数是一个比较复杂的数学概念， 涉及向量空间的内积和无限维向量空间。 为了更好地理解这个概念， 先回到支持向量学习机的最优化问题， 讨论这个问题的另一种求解方法——拉格朗日对偶 。

2.2 拉格朗日对偶

我们在1.4节中介绍了支持向量学习机对应的最优化问题， 具体的公式如下：

​ $$min\frac{1}{2}{\mid \mid w\mid \mid }^2+C\sum _i{\xi }_i$$

​ $$y_i(w\cdot X_i+c)\ge 1-{\xi }_i;{\xi }_i\ge 0$$ (2-2)

随后的1.5节讨论了如何将公式（2-2） 转换为没有限制条件的最优化问题， 但提供的解决方法并不具备普遍性， 也没有触及问题的本质。 现在， 我们将讨论对于这类问题更加简便也更加工程化的解决方法， 这就是在机器学习中应用非常广泛的拉格朗日对偶。 当然这个方法涉及很多深刻的数学知识， 比较复杂， 对数学细节不感兴趣的读者可以跳过其中的数学证明， 记住结论即可（ 见图10） 。

将公式（2-2） 泛化为更加抽象的最优化问题， 如公式（2-3） 所示：

​ $$minf(\theta )$$

​ $$g_i(\theta )\le 0,i=1,...,k$$

​ $$h_i(\theta )=0,i=1,...,l$$ (2-3)

上面的这个问题在学术上被称为原始问题（primal optimization problem）。 基于它定义相应的拉格朗日函数（ Lagrangian或者generalized Lagrangian）， 其中，${\alpha }_i,{\beta }_i$在学术上被称为拉格朗日乘数（Lagrange multiplier）。

​ $$L(\theta ,\alpha ,\beta )=f(\theta )+\sum _i{\alpha }_i{g}_i(\theta )+\sum _i{\beta }_i{h}_i(\theta )$$ (2-4)

接下来， 违反常规将问题搞得“更复杂” 。 不妨设$P(\theta )=ma{x}_{\alpha \ge 0,\beta }L(\theta ,\alpha ,\beta )$ 。当 $\theta$的值满足公式（2-3）中的限制条件时，可以得到$P(\theta )=f(\theta )$ ； 当$\theta$ 的取值不满足限制条件时， 也容易得到 $P(\theta )=\infty$。 因此， 公式（2-3）等价于公式（2-5）这个更复杂的双重最优化问题。

​ $$mi{n}_{\theta }P(\theta )=mi{n}_{\theta }ma{x}_{\alpha \ge 0,\beta }L(\theta ,\alpha ,\beta )$$ (2-5)

现在定义所谓的对偶问题（dual optimization problem） 。 不妨设 $D(\alpha ,\beta )=mi{n}_{\theta }L(\theta ,\alpha ,\beta )$，则公式（ 2-5）的对偶问题为：

​ $$ma{x}_{\alpha \ge 0,\beta }D(\alpha ,\beta )=ma{x}_{\alpha \ge 0,\beta }mi{n}_{\theta }L(\theta ,\alpha ,\beta )$$ (2-6)

在一定条件下（ 这些条件，当然公式（2-2）都满足，原始问题和对偶问题是等价的。 也就是说， 求解公式（2-3）可以转换为求解公式（2-6）。而且更重要的一点， 这两个问题的最优解一定存在， 并满足所谓的卡罗需-库恩-塔克条件（Karush-Kuhn-Tucker conditions， KKT条件） 。

不妨设 $\hat{\theta }$,$\hat{\alpha }$,$\hat{\beta }$是达到最值时的参数值， 即$L(\hat{\theta },\hat{\alpha },\hat{\beta })=mi{n}_{\theta }P(\theta )=ma{x}_{\alpha \ge 0,\beta }D(\alpha ,\beta )$ ，那么KKT条件如公式（2-7）所示：

​ $$\frac{\partial L}{\partial \theta }(\hat{\theta },\hat{\alpha },\hat{\beta })=0$$

​ $$\frac{\partial L}{\partial \beta }(\hat{\theta },\hat{\alpha },\hat{\beta })=0$$

​ $$\widehat{{\alpha }_i}{g}_i(\hat{\theta })=0$$

​ $$g_i(\hat{\theta })\le 0$$

​ $$\widehat{{\alpha }_i}\ge 0$$ （2-7）

有了上面的数学基础， 现将公式（2-2）转换为相应的对偶问题。 需要注意的是， 公式（ 2-2）里只有 $g_i(\hat{\theta })\le 0$这一类限制条件。 首先定义相应的拉格朗日函数：

​ $$L(w,c,\xi ,\alpha ,\gamma )=\frac{1}{2}{\mid \mid w\mid \mid }^2+C\sum _i{\xi }_i-\sum _i{\alpha }_i[y_i(w\cdot X_i+c)-1+{\xi }_i]-\sum _i{\gamma }_i{\xi }_i$$ （2-8）

于是对偶函数为$D(\alpha ,\gamma )=mi{n}_{w,c,\xi }L(w,c,\xi ,\alpha ,\gamma )$， 应用公式（2-7）中的第一个等式可以得到：

​ $$\frac{\partial L}{\partial w}=0=>\hat{w}=\sum _i{\hat{\alpha }}_i{y}_i{X}_i$$

​ $$\frac{\partial L}{\partial \xi }=0=>C-{\hat{\alpha }}_i-{\hat{\gamma }}_i=0$$

​ $$\frac{\partial L}{\partial c}=0=>\sum _i{y}_i{\hat{\alpha }}_i=0$$ （2-9）

注意到$\hat{w}={\sum }_i{\hat{\alpha }}_i{y}_i{X}_i$，于是模型的预测公式可以写为公式（2-10），其中$X_i\cdot X_j$表示两个向量之间的内积 。

​ $${\hat{y}}_j=sign(\sum _i{\hat{\alpha }}_i{y}_i(X_i\cdot X_j)+\hat{c})$$ （2-10）

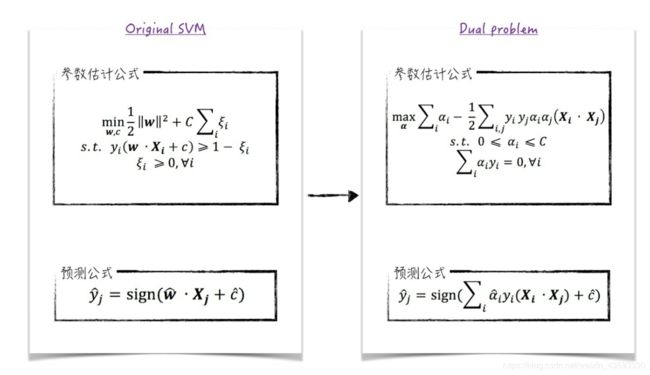
经过一些比较复杂的计算， 可以得到支持向量学习机的对偶形式（ 公式（ 2-11））， 整个过程如图10所示。

​ $$ma{x}_{\alpha }\sum _i{\alpha }_i-\frac{1}{2}\sum _{i,j}{y}_i{y}_j{\alpha }_i{\alpha }_j(X_i\cdot X_j)$$

​ $$0\le {\alpha }_i\le C，\sum _i{\alpha }_i{y}_i=0$$ （2-11）

​ 图10

2.3 支持向量

将模型转换成相应的对偶问题能帮助我们更深刻地理解模型。 比如公式（2-10） 就清楚地展示了支持向量学习机是如何使用训练数据的， 以及后者是如何影响预测结果的。

• 首先， 分别计算被预测点$X_j$ 和训练数据里各点$X_i$ 的内积， 即$X_i\cdot X_j$。
• 然后， 将这些得到的内积作为权重去加权平均训练数据里的因变量 ${\hat{\alpha }}_i{y}_i$， 得到最终的预测值。

事实上， 由于向量内积$X_i\cdot X_j$ 在某种程度上可以度量 $X_j$和 $X_i$的相似度， 因此支持向量学习机（ 几乎所有的算法模型也都这样） 做模型的思路可以理解为： 寻找与被预测数据相似的训练数据， 并将相应的因变量加权平均得到最后的预测值。 由此可以看到， 模型在本质上是训练数据的一种数学组合（ 常常是线性组合）， 数据质量在很大程度上决定了最后效果的好坏。 因此在机器学习领域有这样一个共识： 数据和特征决定了机器学习的上限， 而模型和算法只是逼近这个上限而已。

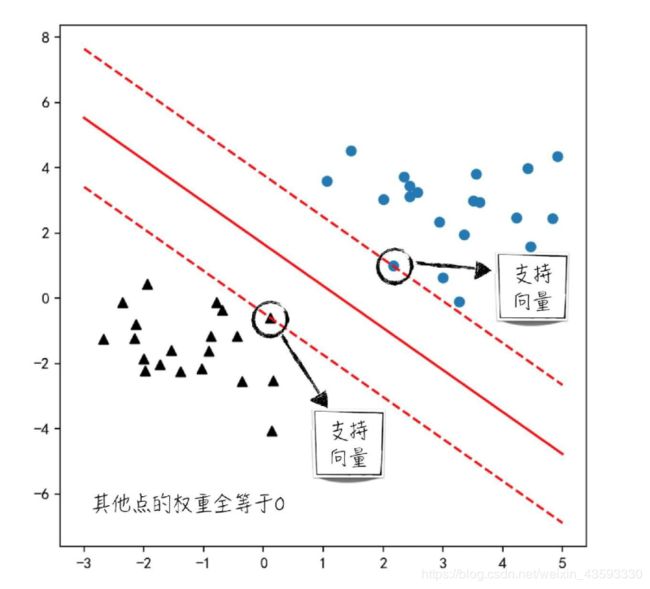
回到公式（2-10），从表面上来看， 每一个训练数据都会对预测结果产生影响， 但实际上并非如此。 不妨假设训练数据$i$ 满足 $y_i(\hat{w}\cdot X_i+\hat{c})>1$ ，相应的约束条件为$g_i=1-y_i(\hat{w}\cdot X_i+\hat{c})-{\hat{\xi }}_i$ 。 根据KKT条件， 可得 $\widehat{{\alpha }_i}{g}_i=0$，而$g_i=1-y_i(\hat{w}\cdot X_i+\hat{c})-{\hat{\xi }}_i<0$ ， 这说明$\widehat{{\alpha }_i}=0$。

以二维空间为例， 直观理解这一结论： 对于如图11所示的模型结果， 若数据落在两条虚线外， 则它的权重肯定等于0； 只有落在虚线上或两条虚线内的点， 它的权重才有可能不等于0。 这些点在学术上被称为支持向量（support vectors），这也是支持向量学习机这个名字的来源。

​ 图11

2.4 核函数的定义：优化运算

在研究了支持向量学习机的对偶问题后， 接下来就将讨论什么是核函数以及如何使用它解决非线性分类问题。

与2.1节中的记号一致， 不妨假设原始数据为$\{X_i,y_i\}$ 以及非线性的空间变换为 $\varphi$， 那么支持向量学习机的实际训练数据是 $\{\varphi (X_i),y_i\}$。 如果借助模型的对偶问题（ 事实上， 只需将图10中的内积运算$X_i\cdot X_j$ 替换为 $\varphi (X_i)\cdot \varphi (X_j)$就可以得到空间变换后的最优化问题）， 完成模型训练其实并不需要$\varphi$的具体表达式， 只需知道内积$\varphi (X_i)\cdot \varphi (X_j)$。 这就是所谓的核函数， 记为$K(X_i\cdot X_j)$ 。
​ $$K(X_i\cdot X_j)=\varphi (X_i)\cdot \varphi (X_j)$$ （2-12）

通过一个简单的例子来直观感受一下核函数。 在2.1节中， 我们通过坐标的平方来做空间变换， 现在将它稍稍复杂化一点。 定义$\varphi (X_i)=(x_{1,i}^2,x_{2,i}^2,\sqrt{2}{x}_{1,i}{x}_{2,i})$ ， 则可以证明它的核函数如下：

​ $$\varphi (X_i)\cdot \varphi (X_j)=x_{1,i}^2{x}_{1,j}^2+x_{2,i}^2{x}_{2,j}^2+\sqrt{2}{x}_{1,i}{x}_{2,i}{x}_{1,j}{x}_{2,j}$$

​ $$\varphi (X_i)\cdot \varphi (X_j)=(X_i\cdot X_j{)}^2=K(X_i\cdot X_j)$$ （2-13）

对于一个已知的空间变换 $\varphi$，使用核函数比直接计算向量内积 $\varphi (X_i)\cdot \varphi (X_j)$更加高效。 特别是当数据$\varphi (X_i)$的维度很高时， 核函数能极大地减少模型的运算量。 反过来， 当在模型里使用某个核函数$K(X_i\cdot X_j)$ 时， 我们在不知不觉间完成了原始空间到某个新空间的映射（ 通常并不知道空间变换的具体形式）， 并在此过程中， 将原本几乎无法解决的非线性问题转换为容易解决的线性问题， 整个过程就像变魔法一样。
虽然核函数在理论上十分完美， 但在实际应用中， 常常面临如下的两大难题：第一， 如何知道一个函数是否为核函数； 第二， 对于当前的建模数据， 哪个核函数是最合适的。
对于第一个问题， 核函数的证明是比较困难的。 但好在数学家们已经找到了一些对大多数场景都适用的核函数， 具体的细节请参考2.5节。 对于第二个问题，并没有一个特别完美的解决方法。 如果对核函数隐含的空间变换有足够深刻的理解， 可以通过分析问题场景， 选择合适的核函数。 但在实际生产中， 最常用的方法还是将常用的核函数当成超参数（hyperparameter）， 使用网格搜寻（gridsearch）的方法找到效果最好的核函数。

2.5 常用的核函数

常用的核函数被列举在图12中。 由于本章使用scikit-learn搭建模型， 为了便于读者使用开源算法， 在介绍核函数时， 将使用同算法API相同的参数记号。

​ 图12

借助scikit-learn， 在支持向量学习机中使用核函数非常简单。 具体的代码如程序清单2所示。

（1）可以通过类SVC的“kernel”参数选择使用的核函数。 既可以传入核函数名字符串， 如1.6节中的“SVC(kernel='linear')”， 也可以传入算法库里定义好的核函数类， 如第9～ 12行代码所示。 这两种方法的差别在于， 前者支持的核函数选项较少， 比如它不支持Laplacian kernel， 但后者支持。

（2） 对于核函数， SVC还有一些其他的常用参数， 比如“gamma” “coef0”以及“degree”等。 它们对核函数的影响请参考图12。 正如2.4节中讨论的， 这些参数其实都是模型的超参数， 常使用网格搜寻的方法来找到它们最合适的取值。

运行上面的代码， 对图9里的“圆圈” 数据做分类， 可以得到如图13所示的结果。 图中的圆点表示类别1， 三角形表示类别0； 灰色区域表示预测结果等于类别0， 而白色区域为预测结果等于类别1。 图中的实线是分离超平面， 而虚线表示支持向量所在的范围。

模型的结果显示， 线性支持向量学习机的效果很差， 而多项式核函数（ polynomial kernel），高斯核函数（RBF kernel） 和拉普拉斯核函数（Laplacian kernel） 都能比较好地解决这个非线性分类问题。

​ 图13

我们能够比较好地理解为什么多项式核函数对这个问题的效果很好：因为变换后的空间里恰好包含$(x_1^2,x_2^2)$ 。 但为什么高斯核函数和拉普拉斯核函数的效果也不错呢？ 要很严谨地解释这个问题的原因需要比较深厚的数学功底。 因此， 这里只提供一个不太严谨的直观解释。 高斯核函数对应着将数据映射到无限维空间， 虽然这个空间并不包含 $(x_1^2,x_2^2)$， 但数据在变换后的空间里分布得非常“光滑” 。 而“光滑” 的新数据使得很多问题（ 包括图13所示的分类问题） 变得简单， 模型的效果也很好。 这也是为什么说高斯核函数是魔力十足的核函数。 对于拉普拉斯核函数， 虽然它也将数据映射到无限维空间， 但变换后的数据不如高斯核函数那样的“光滑” ， 所以模型效果也通常不如后者。

2.6 Scale variant

前面的章节中主要讨论了支持向量学习机的理论细节。 本节作为介绍这个模型的最后一部分， 将讨论在实际使用支持向量学习机时， 常碰到但又经常被人忽略的一点： 支持向量学习机与线性回归和逻辑回归不同， 它对特征（ 自变量） 的线性变换不稳定。 在学术上， 这一点被称为scale variant。

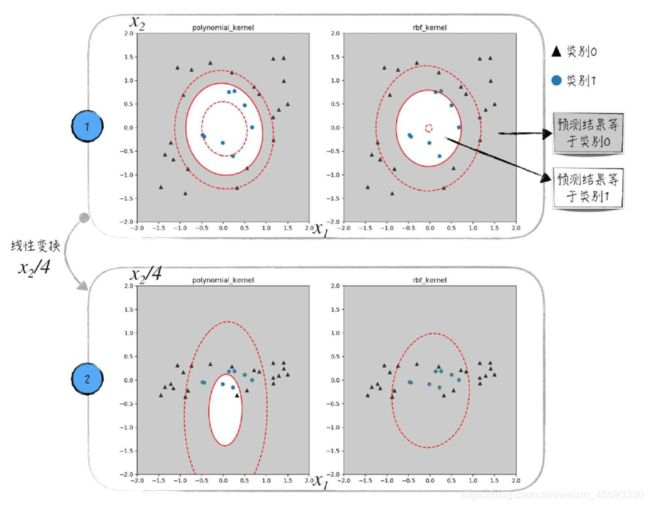
为了便于理解， 先从一个具体的例子开始讲起。 我们沿用2.1节中的非线性分类数据， 这份数据的自变量有两个 $x_1,x_2$。 这两个变量的中心位置和变化幅度一样的， 即它们的期望相同， 方差也相等。 使用支持向量学习机对数据建模， 得到的预测结果来不错， 如图14中的标记1所示。

​ 图14

现在对数据的自变量做线性变换得到新的数据集， 新数据的自变量为$z_1.z_2$ ， 具体的定义如公式（2-14）所示。 在实际生产中， 类似的线性变换是经常发生的， 比如更换变量$x_2$的计数单位。
​ $$z_1=x_1,z_2=x_2/4$$ （2-14）

从直观上来讲， 上面的变换并没有改变数据的相对位置， 只是从整体上将数据“压扁” 了一些， 如图14中的标记2所示。 按理来说， 这个线性变换并不影响分类问题的解决。 但事实上，对于新的数据集， 支持向量学习机的模型效果很差，比如使用高斯核函数时， 所有数据的预测结果都是类别0。

上面的例子说明， 特征的线性变换（ 放大或缩小） 将极大地影响模型的效果，也就是本节开头所提到的， 支持向量学习机对特征的线性变换不稳定。 这是因为从数学上来讲， 支持向量学习机的预测公式为 ${\hat{y}}_j=sign({\sum }_i{\hat{\alpha }}_i{y}_i(\varphi (X_i)\cdot \varphi (X_j))+\hat{c})$ ， 其中参数的估计值依赖于公式（2-15）。

​ $$ma{x}_{\alpha }\sum _i{\alpha }_i-\frac{1}{2}\sum _{i,j}{y}_i{y}_j{\alpha }_i{\alpha }_j[\varphi (X_i)\cdot \varphi (X_j)]$$

​ $$0\le {\alpha }_i\le C，\sum _i{\alpha }_i{y}_i=0$$ （2-15）

可以看到， 无论是参数估计还是做预测都只涉及向量的内积运算， 而后者本身对线性变换是不稳定的。以二维空间里的线性缩放为例， 假设 $X_i=(x_{1,i},x_{2,i})$以及$X_j=(x_{1,j},x_{2,j})$， 则这两个向量之间的内积为$X_i\cdot X_j=x_{1,i}{x}_{1,j}+x_{2,i}{x}_{2,j}$ 。 若将第二个变量扩大10倍， 则相应的数据点变为 $X_i=(x_{1,i},10x_{2,i})$ 以及$X_j=(x_{1,j},10x_{2,j})$ ， 它们的内积为$X_i\cdot X_j=x_{1,i}{x}_{1,j}+100x_{2,i}{x}_{2,j}$ 。 也就是说， 第二个变量的权重是第一个变量的100倍， 而且模型无法修正这种变量间的权重差异。 类似地， 可以证明线性平移， 比如第二个变量加上某个常数， 也有相似地效应。 因此， 线性变换会极大地影响模型的预测结果。
从模型的角度来看这个问题， 上面的例子说明， 如果变量$A$ 的变化幅度（ 标准差） 是变量$B$ 的10倍， 则对于支持向量学习机而言， $A$的重要性是 $B$ 的100倍。 这样的隐含假设显然是不合理的， 会极大地损害模型效果。 为了去掉这个干扰因素， 需要将各个变量归一化后使用。 即针对变量 $x$， 通过如公式（2-16） 所示的线性变换生成期望为0， 方差为1的新变量$xx$ ， 然后使用新变量 $xx$搭建模型。
​ $$xx=(x-\overline{x})/std(x)$$ （2-16）
图14的标记2到标记1就表示： 通过变量归一化， 可以提升模型的预测效果。