最长递增子序列的长度求解并打印(动态规划)
设b[i]是在a[i]为单调递增子序列最后一个元素时,所得最长递增子序列的长度为:

设计思路1(O(n^2)):
1.a数组存储原始数据
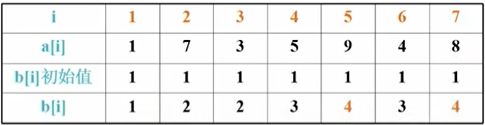
2.b数组存储对应最长上升子序列长度
(比如i=3时,a[i]=3,在i<3中寻找比3小的元素,有1,则b[3]=1+1=2,比如i=5时,a[i]=9,在i<5中寻找比9小的元素,有1,3,5,7比较得到这些满足条件中的b[i]最大值,为3,则b[5]=3+1=4)
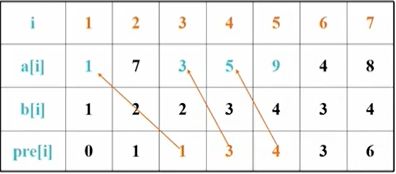
使用pre数组存储最长上升子序列当前元素的上一个元素的下标
#include假设存在一个序列d[1…9] = 2 1 5 3 6 4 8 9 7,可以看出来它的LIS长度为5。
我们定义一个序列B,然后令 i = 1 to 9 逐个考察这个序列。
此外,我们用一个变量Len来记录现在最长算到多少了
首先,把d[1]有序地放到B里,令B[1] = 2,就是说当只有1一个数字2的时候,长度为1的LIS的最小末尾是2。这时Len=1
然后,把d[2]有序地放到B里,令B[1] = 1,就是说长度为1的LIS的最小末尾是1,d[1]=2已经没用了,很容易理解吧。这时Len=1
接着,d[3] = 5,d[3]>B[1],所以令B[1+1]=B[2]=d[3]=5,就是说长度为2的LIS的最小末尾是5,很容易理解吧。这时候B[1…2] = 1, 5,Len=2
再来,d[4] = 3,它正好加在1,5之间,放在1的位置显然不合适,因为1小于3,长度为1的LIS最小末尾应该是1,这样很容易推知,长度为2的LIS最小末尾是3,于是可以把5淘汰掉,这时候B[1…2] = 1, 3,Len = 2
继续,d[5] = 6,它在3后面,因为B[2] = 3, 而6在3后面,于是很容易可以推知B[3] = 6, 这时B[1…3] = 1, 3, 6, Len = 3 。
第6个, d[6] = 4,你看它在3和6之间,于是我们就可以把6替换掉,得到B[3] = 4。B[1…3] = 1, 3, 4, Len继续等于3
第7个, d[7] = 8,比4大,B[4] = 8。Len变成4了
第8个, d[8] = 9,得到B[5] = 9,嗯。Len继续增大,到5了。
最后一个, d[9] = 7,它在B[3] = 4和B[4] = 8之间,所以我们知道,最新的B[4] =7,B[1…5] = 1, 3, 4, 7, 9,Len = 5。
所以LIS的长度为5。
需要特别注意的是:
最终得到的B数组中的1,3,4,7,9不是LIS,它只是存储的 对应长度LIS的最小末尾。有了这个末尾,我们就可以一个一个地插入数据。虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义,但是如果后面再出现两个数字 8 和 9,那么就可以把8更新到d[5], 9更新到d[6],得出LIS的长度为6。
#include参考博文:
https://www.felix021.com/blog/read.php?1587
