基于Transformer模型的智能问答原理详解（学习笔记）

文章均从个人微信公众号“ AI牛逼顿”转载，文末扫码，欢迎关注！

---

距离上一篇的对联生成有段日子了，年已过，对联就靠边站啦，这回说说智能问答这个话题。其实两者是同一类问题，你可以把写下联看成是回答上联的问题。所以上篇文章介绍的模型是可以直接用来进行智能问答的。今天要介绍的模型框架依然是encoder-decoder，不过模型只采用attention机制。目的就是要避免使用RNN结构，提高并行效率（RNN的网络结构决定了它只能串行计算），同时还要保证最终的实验效果。

一、模型概览

图一

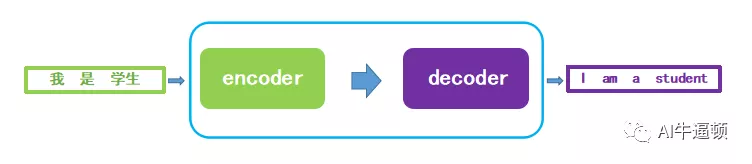
图一就是Transformer模型的框架，不过这里的encoder和decoder不再是RNN结构，拆开来看，细节如图二：

图二

原始论文里，作者设置了6层encoder与6层decoder结构。至于为什么是6，这就是一个超参数而已，可以根据实际情况设置为其他值。从图二中可以看到，计算流程是：输入的句子经过逐层编码后，最上层的encoder会输出中间结果，这个中间结果在每一层decoder中都会用到。同时decoder的计算也是从下往上进行，直到最后输出预测结果。这里省略的是最下层decoder的输入：如果是训练过程，输入则是真实的目标句子；如果是预测过程，第一个输入开始标识符，预测下一个词，并且把这个词作为输入，再预测下一个词。

二、模型细节

每一层的encoder结构完全一样，同样的，每一层的decoder结构也完全一样。另外，decoder的结构和encoder的结构也有相同之处。这里我们重点介绍encoder。

图三

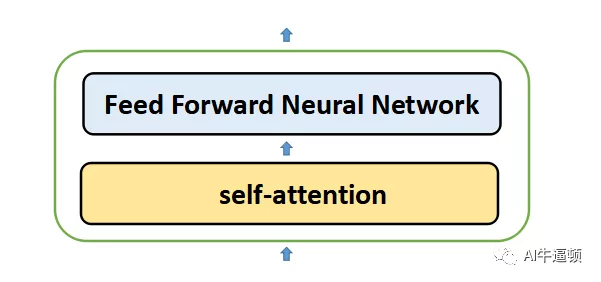
如图三所示，每个encoder里面都有两个子层，分别是自注意力层（self-attention）和全连接层（Feed Forward Neural Network）。

那么数据是如何在子层中进行计算的呢？这里用第一层encoder来进行说明，如图四所示。

图四

最底下的输入是词向量，接着进行自注意力机制的计算，输出中间结果z，然后再输入全连接层进行计算，最后输出结果。该结果就是第二层encoder的输入，以此类推。

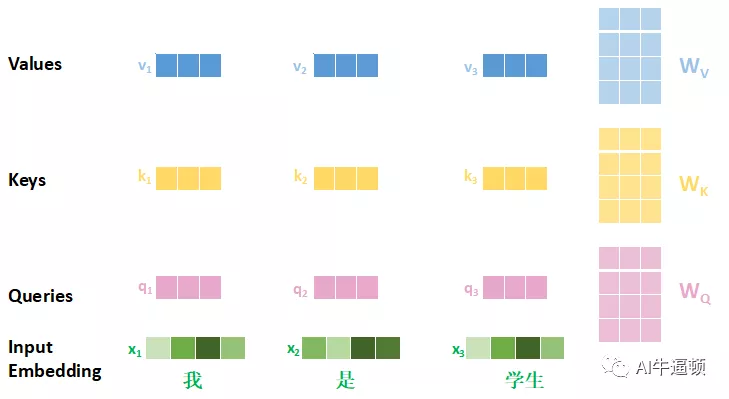
子层里面的核心就是自注意力层，接下来就详细说明自注意力层的计算细节。进行自注意力机制的计算，首先要根据输入，计算出三个新的向量：查询向量（Queries）、键向量（Keys）、值向量（Values）。先来看看这三个向量长啥样，如图五：

图五

每个q向量都是对应的x向量与WQ矩阵相乘的结果；每个k向量都是对应的x向量与WK矩阵相乘的结果；每个v向量都是对应的x向量与WV矩阵相乘的结果。这三个矩阵是可以训练出来的。在原始论文里，x向量的维度是512，q，k，v的维度都是64，所以三个矩阵的维度都是512*64。这里用方格的个数加以区分。

三个向量的作用在图六中可以看到，至于为啥叫这个名字，个人觉得应该是体现了计算过程中的匹配这种思想。搞清楚了这几个向量之后，就来开始说说自注意力计算的过程啦。图六里的计算顺序自下而上。

图六

（1）把得到的q1向量分别与三个（这里假设的输入只有三个词）k向量进行数量积计算，结果如图六中假设的值；

（2）接着把每个值除以8，这里8的来历为：k的维度的平方根。原始论文里，设置的k的维度是64，所以开方后等于8。至于为什么要除以8，论文作者指出这样做能使梯度更稳定。最后再用softmax函数算出结果，如图六中的小数。

（3）softmax函数的结果可以理解为权重，然后将这三个权重与对应的三个v向量相乘，最后再相加，得到输出的中间结果z向量。这里的每个z向量的维度都是64。

从这个计算过程中，能体会出向量的名称含义：通过向量的数量积计算，体现出两个向量的匹配程度，然后利用这个程度来影响权重的大小，最后把每个词的值向量加权求和得到自注意力的结果。

有个细节，不知道大家注意到没有：图四里，z向量的维度和输入向量x是一样的，但是咱们在图六中计算出来的结果，z向量和x向量维度不同，图六中也画出了这种差别。问题出在哪？不着急，这里还有一个操作：多头注意力（Multi-Head Attention）

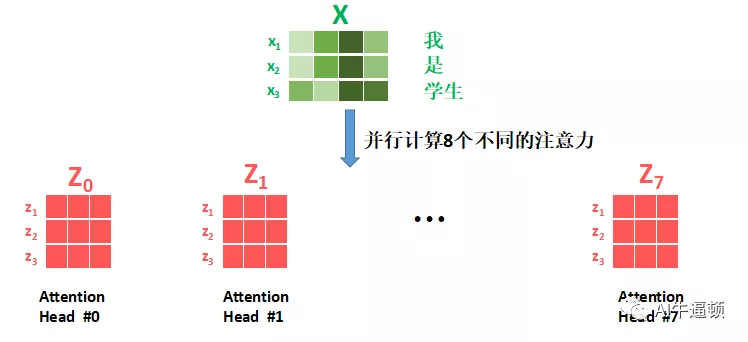
这是啥意思呢，通俗来说，就是再把刚才的自注意力计算过程再并行的计算几个！并行计算的时候，用的是相同的x向量，但是W矩阵不同，所以k，q，v向量是不同的，显然并行计算的结果z向量是不同的。作者在论文里并行计算了8个，也就是说对同一个输入x1向量，有8个不同的z1向量输出，然后再把这8个向量拼接起来，维度就又回到512了！具体看图解。

图七

图七采用了矩阵的方式来画图。图六只是展示了一个x向量进行计算的详情，如果要进行一个输入句子的自注意力计算，变成矩阵乘法就可以了。首先解析各个字母的含义：

（1）大写X是输入句子的词向量矩阵，行数代表句子里词的个数，列数代表词向量的维度，论文里设定的词向量维度是512；

（2）大写Z0 ~ Z7是8个attention矩阵，形状是完全相同的。每个矩阵的行数就是输入句子里词的个数，列数在论文里设定为64。

有了上面这两点的说明，大家可以想到，如果把Z0 ~ Z7按顺序拼接起来，得到的矩阵的列数是不是512？当然了，论文里并不是直接把这个拼接的矩阵作为全连接层的输入，而是再和一个矩阵相乘，进行线性组合，充分利用这个‘组装矩阵’的信息。可以很容易的想到，这个进行相乘的矩阵，其维度是512*512。

说完了这里最核心的attention计算，我们回过头来再看看，这里的Multi-Head Attention思想很类似于卷积神经网络里的‘通道’的概念：把图片进行卷积操作，考虑图片的三个通道，每个通道都有其特定的信息要提取。最后把提取的特征进行汇总，完成整个卷积部分的计算。

核心部分说完了，头脑有没有嗡嗡作响呢？我们再来完善一些细节，那么第一层的encoder就全部说完了。

考虑一个问题：句子里的词毕竟是有语序的，可是咱们这里的自注意力计算，好像压根没用到语序的信息。由于没有使用RNN这样的序列网络结构，所以作者设计一个位置编码向量。这个向量的值能体现每个词的位置信息。把这个向量和词向量相加，结果就可以体现出词的综合信息啦。位置编码向量的计算方法如下：

图八

挨个介绍每个符号的含义：

（1）PE就是我们说的位置编码向量，该向量是要和原始词向量x相加的，所以维度肯定和x一样，按照论文里的参数，这个维度是512。

（2）pos就是每个词在句子里的序号，咱们这个例子里，输入句子有3个词，所以pos的取值就是0,1,2。

（3）i就是向量里每个维度的序号，i从0取值到511，dim是512（论文里设定的参数）。

整个计算表达式里，区别就是正弦和余弦。在向量维度的偶数位置，用正弦计算，向量维度的奇数位置用余弦计算。

另外，论文里还提到，在接全连接层之前，还接一个残差网络和正则化操作。图九则是第一层encoder里的全部细节：

图九

（1）最下层的是词向量，输入到encoder单元之前，要与位置编码（Positional Encoding）进行相加。

（2）图中的黄色向量就是融合了位置编码之后的词向量，进行自注意力机制计算后，输出三个z向量。

（3）论文里提到的残差网络与正则化过程，就是图中的Add & Normalize层。图中的X + Z，是把三个黄色的向量组成矩阵X，把z向量组成矩阵Z，然后进行残差网络计算与正则化过程，其输出的结果就可以进入全连接层。

（4）全连接层输出的结果再经过残差网络与正则化，就是整个encoder #1的输出啦！！！这个输出就是encoder #2的输入了，唯一的区别就是不用再融合位置编码信息了。后续几层的encoder，里面计算过程则和图九方框里的流程完全一样。

恭喜各位看官，到这里，核心部分就基本说完了。最后再次从整体上看看全部的计算流程：

图十
（此图是网上的截图，与前面的图有所差异）

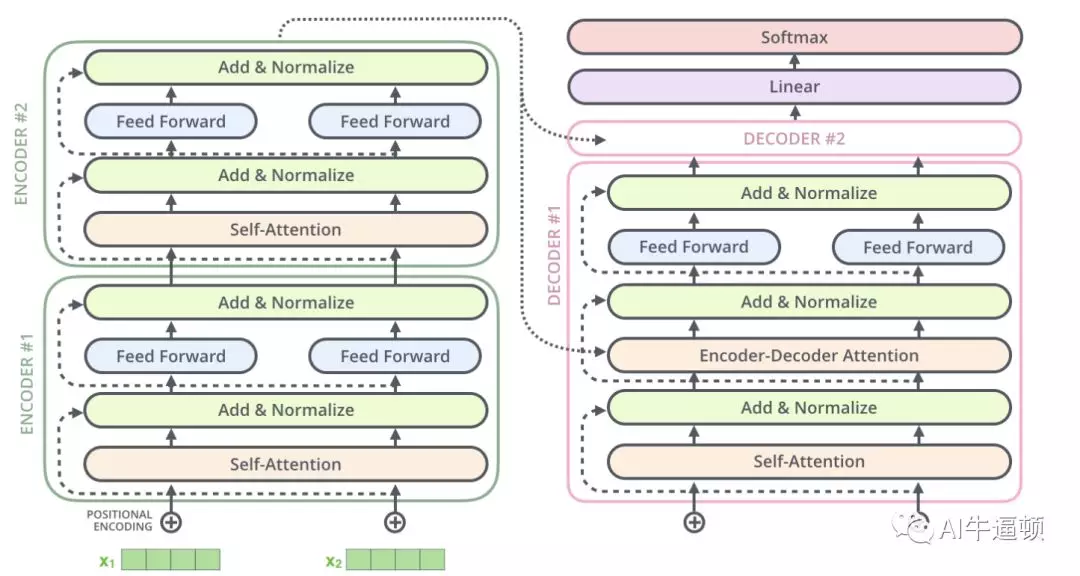
图十就是全部计算流程的细节了。图中以两层encoder与两层decoder来进行说明。图中给出了decoder的细节以及计算流程。

可以看到，decoder和encoder非常相似，只是多了一个encoder-decoder-attention子层，该子层就是计算encoder和decoder之间的注意力（可以回顾上篇文章里的注意力机制，不是自注意力机制！！！）。其他的计算过程完全等同于encoder。从图中可以看到，每一层decoder里的encoder-decoder-attention子层的计算，都要用到encoder部分的最后一层的输出。

decoder部分的最上层为softmax层，输出的就是词表里每个词的概率。在训练阶段，根据这个输出，优化交叉熵，就能不断迭代优化整个模型。

三、学习体会

穷则算法优化，达则给老子run！

谷歌是既有硬件，又有数据，还不断的优化算法，总能捣鼓出牛逼哄哄的模型，就服你！至于为什么要设计这样的模型，参数为什么这样设置，个人感觉就是因为实验的结果靠谱，所以就是这样。或许这正是大数据时代背景下，数据驱动的特点吧。

另外，代码部分还在调试，初期运行后，回答的问题就是智障！可能原因在于数据量很小，迭代次数有限造成的。所以本次就不上传代码了。大家可以在GitHub上搜到TensorFlow版本的Transformer示例代码。

 

 

参考：

https://www.jianshu.com/p/923c8b489604

https://jalammar.github.io/illustrated-transformer/

千里之行始于足下！定期分享人工智能的干货，通俗展现原理和案例实现，并探索案例在中学物理教育过程中的使用。还有各种有趣的物理科普哟。坚持原创分享！坚持理解并吸收后的转发分享！欢迎大家的关注与交流。