姿态旋转与坐标变换

旋转还是变换 ？

作为SLAM中位姿估计的重要内容，姿态的表示方法多种多样，估计精度对系统性能的影响也比位置重要的多。众所周知，姿态的描述方法包括等效旋转矢量、欧拉角、旋转矩阵、姿态四元数等等，有大量成熟的文献描述了这些方法的详细定义和相互之间的转换关系。但遗憾的是，这一看似成熟的领域却依旧是实际应用中错误的重灾区。这一现象的原因，归根结底，在于相关概念的混乱，其中最典型的，就是“空间旋转”和“坐标变换”。因此，在深入讨论姿态表示的相关概念之前，我们需要首先明确，我们所谈论的“姿态表示”，到底是什么？

首先我们来考虑第一种情况，记坐标系$\mathbf{f}$下一个空间矢量的坐标为${\mathbf{v}}^f$，上标表示矢量所在的坐标系；坐标系$\mathbf{f}$保持不变，记该矢量绕$z$轴旋转$\frac{\pi }{2}$后的矢量为${\mathbf{v}}^{\prime f}$，由线性代数的知识我们知道，两者之间的关系可以由一个矩阵表示，即：${\mathbf{v}}^{\prime f}={\mathbf{R}}_1{\mathbf{v}}^f$。

接下来我们考虑第二种情况，同样记坐标系$\mathbf{f}$下一个空间矢量的坐标为${\mathbf{v}}^f$，现在保持矢量不变，将坐标系$\mathbf{f}$绕$z$轴旋转$\frac{\pi }{2}$后得到坐标系${\mathbf{f}}_1$，同样可以用一个矩阵表示空间矢量$\mathbf{v}$在两个坐标系下的关系：${\mathbf{v}}^{f_1}={\mathbf{R}}_2{\mathbf{v}}^f$。

显然，直觉告诉我们矩阵${\mathbf{R}}_1$和${\mathbf{R}}_2$并不一样，那两者之间有什么关系呢？

坐标旋转/变换矩阵（Rotation Matrix）

矩阵${\mathbf{R}}_1$表示空间矢量的旋转过程，称为矢量旋转矩阵；与之相对，矩阵${\mathbf{R}}_2$表示坐标系的旋转过程，矢量本身并没有旋转，只是在不同坐标系下的坐标表示不同，因此称为坐标变换矩阵，根据旋转的可逆性，显然有${\mathbf{R}}_1{\mathbf{R}}_2=\mathbf{I}$。这里请大家牢记并理清这两个矩阵定义上的不同，在后续我们讨论各种姿态表示方法之间的转换关系时，一定要首先明确针对的是旋转还是变换，否则将得到完全相反的结论。

这里需要说明，完整的坐标变换矩阵$\mathbf{T}$为齐次坐标（Homogeneous Coordinates）形式，包括这里所说的旋转变换矩阵$\mathbf{R}$和表示坐标系原点变化的平移变换矢量$\mathbf{t}$两部分，即$\mathbf{T}=[\mathbf{R}|\mathbf{t}]$。但由于本文我们只讨论旋转的相关内容，为了描述方便，以下均将$\mathbf{R}$简称为变换矩阵。

等效旋转矢量（Axis-Angle）

使用矩阵来表示旋转存在过参数化问题（对称矩阵的自由度为6维，但实际旋转的自由度只有3维），且难以直观的表示矢量之间的旋转关系。根据刚体运动学的相关知识，有限次的旋转都可以等效为一个旋转轴和一个旋转角的单次旋转。记该单次旋转对应的旋转轴为$\mathbf{k}$，旋转角为$\theta$，则矢量$\mathbf{k}n$称为等效旋转矢量或轴角（Axis-Angle）。

罗德里格斯公式（Rodrigues’s Formula）

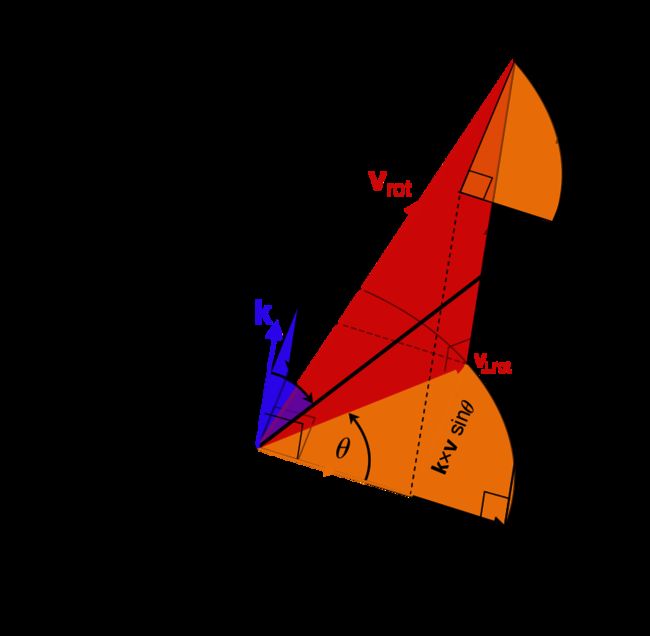
回到上面的问题，旋转前后的矢量之间的关系如何使用等效旋转矢量表示呢？上图表示了同一个坐标系下矢量旋转前后的分解关系，由于所有矢量均在同一个坐标系下表示，为了书写方便，这里我们省略上标$f$，记旋转前后的矢量分别为$\mathbf{v}$和${\mathbf{v}}^{\prime }$，对应的旋转矢量为$\mathbf{k}\theta$。首先我们将矢量分别投影到旋转矢量的垂直方向和平行方向，得到垂直分量${\mathbf{v}}_{\perp }$和平行分量${\mathbf{v}}_{\parallel }$。平行分量可以由向量内积得到：
$${\mathbf{v}}_{\parallel }=\left(\mathbf{v}\cdot \mathbf{k}\right)\mathbf{k}\text{\hspace{1em}(1)}$$
垂直分量${\mathbf{v}}_{\perp }$则可根据拉格朗日公式$\mathbf{a}\times (\mathbf{b}\times \mathbf{c})=\mathbf{b}(\mathbf{a}\cdot \mathbf{c})-\mathbf{c}(\mathbf{a}\cdot \mathbf{b})$得到:
$${\mathbf{v}}_{\perp }=\mathbf{v}-\left(\mathbf{v}\cdot \mathbf{k}\right)\mathbf{k}=-\mathbf{k}\times (\mathbf{k}\times \mathbf{v})\text{\hspace{1em}(2)}$$
平行分量在旋转过程中保持不变${\mathbf{v}}_{\parallel }^{\prime }={\mathbf{v}}_{\parallel }$，旋转后的垂直分量为：
$${\mathbf{v}}_{\perp }^{\prime }={\mathbf{v}}_{\perp }\cos \theta +\mathbf{k}\times {\mathbf{v}}_{\perp }\sin \theta \text{\hspace{1em}(3)}$$
将${\mathbf{v}}_{\perp }=\mathbf{v}-{\mathbf{v}}_{\parallel }$带入式$(3)$并注意到$\mathbf{k}\times {\mathbf{v}}_{\parallel }=0$得到：
$$\begin{array}{rl}{\mathbf{v}}^{\prime }& ={\mathbf{v}}_{\parallel }^{\prime }+{\mathbf{v}}_{\perp }^{\prime }\\ & ={\mathbf{v}}_{\parallel }+(\mathbf{v}-{\mathbf{v}}_{\parallel })\cos \theta +\mathbf{k}\times (\mathbf{v}-{\mathbf{v}}_{\parallel })\sin \theta \\ & =\cos \theta \mathbf{v}+(1-\cos \theta ){\mathbf{v}}_{\parallel }+\sin \theta \mathbf{k}\times \mathbf{v}\\ & =\cos \theta \mathbf{v}+(1-\cos \theta )(\mathbf{v}\cdot \mathbf{k})\mathbf{k}+\sin \theta \mathbf{k}\times \mathbf{v}\end{array}\text{\hspace{1em}(4)}$$
由于$(\mathbf{v}\cdot \mathbf{k})=\mathbf{k}{\mathbf{k}}^T\mathbf{v}$，带入上式，并与$\mathbf{v}’=\mathbf{R}\mathbf{v}$联立，可以得到旋转矩阵$\mathbf{R}$的表达式为：
$$\mathbf{R}=\cos \theta \mathbf{I}+(1-\cos \theta )\mathbf{k}{\mathbf{k}}^T+\sin \theta {\mathbf{k}}^{\wedge }\text{\hspace{1em}(5)}$$
至此，我们得到了使用等效旋转矢量表示的旋转前后矢量坐标之间的关系，式$(5)$称为罗德里格斯公式（Rodrigues’s Formula），表征了等效旋转矢量和旋转矩阵之间的关系。

注意这里的矩阵$\mathbf{R}$是旋转矩阵而非变换矩阵。有时候（甚至更多时候）我们会用等效旋转矢量表示坐标系的旋转而非矢量的旋转。例如，坐标系${\mathbf{f}}_1$经过等效旋转矢量$\mathbf{k}\theta$旋转后，得到坐标系${\mathbf{f}}_2$，则由罗德里格斯计算得到的矩阵$\mathbf{R}$表征的是${\mathbf{f}}_2\to {\mathbf{f}}_1$的坐标变换，即：
$${\mathbf{v}}^{f_1}=\mathbf{R}{\mathbf{v}}^{f_2}\text{\hspace{1em}(6)}$$

汉密尔顿四元数（Hamilton Quaternion）

使用等效旋转矢量表示姿态依旧存在一个问题——“奇异性”，因此我们需要找到一种即紧凑，又不容易产生奇异的方式描述姿态。由于复数天然可以用来表示复平面上的旋转，使用复数表示空间三维旋转的方式也应运而生，即姿态四元数。

一个完整的姿态四元数包含一个实部和三个虚部，且模长为1：
$$\begin{array}{rl}& \mathbf{q}=q_w+q_x\mathbf{i}+q_y\mathbf{j}+q_z\mathbf{k}\\ & \Vert \mathbf{q}\Vert =1\end{array}\text{\hspace{1em}(7)}$$
这里我们采用的是实部在前，虚部在后的方式，称为汉密尔顿四元数（Hamilton Quaternion）；同样亦存在实部位于最后的定义方式（例如后面要将的C++线性代数库Eigen），在使用四元数相关公式时（例如四元数微分、四元数和旋转矩阵的转换等）一定要明确四元数分量的排列顺序。

四元数和旋转矢量之间的关系定义为：
$$\mathbf{q}=\cos \frac{\theta }{2}+\sin \frac{\theta }{2}\mathbf{i}+\sin \frac{\theta }{2}\mathbf{j}+\sin \frac{\theta }{2}\mathbf{k}\text{\hspace{1em}(8)}$$
由式$(8)$得到的四元数称为旋转四元数，使用旋转四元数进行矢量旋转的操作为：
$${\mathbf{v}}^{\prime f}=\mathbf{q}{\mathbf{v}}^f{\mathbf{q}}^{\ast }\text{\hspace{1em}(9)}$$
式中，${\mathbf{q}}^{\ast }=\cos \frac{\theta }{2}-\sin \frac{\theta }{2}\mathbf{i}-\sin \frac{\theta }{2}\mathbf{j}-\sin \frac{\theta }{2}\mathbf{k}$为$\mathbf{q}$的共轭四元数。

同样，当四元数$\mathbf{q}$表示坐标系${\mathbf{f}}_1\to {\mathbf{f}}_2$的旋转时，式$(9)$表征的是${\mathbf{f}}_2\to {\mathbf{f}}_1$的坐标变换关系，即：
$${\mathbf{v}}^{f_1}=\mathbf{q}{\mathbf{v}}^{f_2}{\mathbf{q}}^{\ast }\text{\hspace{1em}(10)}$$
由于四元数与其共轭表示相反方向的旋转，自然有${\mathbf{v}}^{f_2}={\mathbf{q}}^{\ast }{\mathbf{v}}^{f_1}\mathbf{q}$，将其与式$(6)$联立可以得到坐标系${\mathbf{f}}_1\to {\mathbf{f}}_2$之间旋转四元数${\mathbf{q}}_{f_1}^{f_2}$和坐标变换矩阵${\mathbf{R}}_{f_1}^{f_2}$之间的关系为：
$$\begin{array}{rl}{\mathbf{R}}_{f_1}^{f_2}\left[\begin{array}{c}x\\ y\\ z\end{array}\right]& =\left[\begin{array}{c}\left(q_w^2+q_x^2-q_y^2-q_z^2\right)x+2\left(q_w{q}_z+q_x{q}_y\right)y+2\left(q_x{q}_z-q_2{q}_y\right)z\\ 2\left(q_x{q}_y-q_w{q}_z\right)x+\left(q_w^2-q_x^2+q_y^2-q_z^2\right)y+2\left(q_w{q}_x+q_y{q}_z\right)z\\ 2\left(q_w{q}_y-q_x{q}_z\right)x+2\left(q_y{q}_z-q_w{q}_x\right)y+\left(q_w^2-q_x^2-q_y^2+q_z^2\right)z\end{array}\right]\\ & =\left[\begin{array}{ccc}\left(q_w^2+q_x^2-q_y^2-q_z^2\right)& 2\left(q_w{q}_z+q_x{q}_y\right)& 2\left(q_x{q}_z-q_2{q}_y\right)\\ 2\left(q_x{q}_y-q_w{q}_z\right)& \left(q_w^2-q_x^2+q_y^2-q_z^2\right)& 2\left(q_w{q}_x+q_y{q}_z\right)\\ 2\left(q_w{q}_y-q_x{q}_z\right)& 2\left(q_y{q}_z-q_w{q}_x\right)& \left(q_w^2-q_x^2-q_y^2+q_z^2\right)\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\end{array}\right]\end{array}\text{\hspace{1em}(11)}$$

欧拉角

由于解算存在奇异，且对转序敏感，欧拉角在实际的姿态解算中应用并不多；但欧拉角的表示方式比较符合易于想象，因此在大多数情况下只用于结果的显示和保存，这里暂且略过不谈。

Eigen中的姿态表示

作为应用最广泛的C++开源线性代数运算库，几何模块Eigen::Geometry提供了刚体运动相关的各项功能，所有角度的单位以弧度（radius）表示。

变换矩阵

Eigen中的坐标变换矩阵即普通的3x3双精度矩阵Matrix3d，构造方式和普通的矩阵一致，例如：

Eigen::Matrix3d rotation_matrix;
rotation_matrix << x_00,x_01,x_02,x_10,x_11,x_12,x_20,x_21,x_22;

等效旋转矢量

Eigen中的等效旋转矢量拥有自己的专属模板类AngelAxis，一般使用预定义好的double型子类AngleAxisd，构造方式如下：

Eigen::AngleAxisd rvec(double angle, Eigen::Vector3d axis)//直接由参数构造
Eigen::AngleAxisd rvec(rotation_matrix)// 通过变换矩阵构造

需要注意的是构造时传入的变换矩阵为逆矩阵，即若构造${\mathbf{f}}_1\to {\mathbf{f}}_2$的旋转矢量，则需要传入变换矩阵${\mathbf{R}}_{f_2}^{f_1}$。构造完成后，使用成员函数toRotationMatrix()可以获得逆变换矩阵${\mathbf{R}}_{f_2}^{f_1}$。

旋转四元数

Eigen中的旋转四元数归属于模板类Quaternion，一般同样使用预定好的double型子类Quaterniond，旋转四元数可以直接由旋转矢量构建：

Eigen::Quaterniond q(rvec)// 直接由旋转矢量构建
Eigen::Quaterniond q1(q_w, q_x, q_y, q_z)// 直接由分量构建；
Eigen::Quaterniond q2(rotation_matrix)// 直接由变换矩阵构建；

• 使用旋转矢量构造式，获得的四元数为与旋转矢量一致的旋转四元数；
• 使用变换矩阵构造时，与旋转矢量一样需要传入逆矩阵；
• 由分量构造时，按照实部在前的顺序传入，但在Eigen内部存储时，采用的是实部在后的存储格式。

使用Eigen进行矢量旋转

Eigen中使用旋转矢量和四元数对矢量进行运算时，由于操作符*重载为矩阵运算方式，因此只接收左乘操作，运算表示旋转而非变换。

Eigen::AngleAxisd rvec(M_PI/2.0, Eigen::VEctor3d(0, 0, 1)); // 绕z轴旋转pi/2
Eigen::Matrix3d R = rvec.toRotationMatrix();
Eigen::Quaterniond q(rvec);

Eigen::Vector3d a{1., 0., 0.}
std::cout << "q * a: " << std::endl << q * a << std:: endl; 
std::cout << "R * a: " << std::endl << R * a <<std::endl;
std::cout << "rvec * a" << std::endl << rvec * a << std::endl;

在上面这个例子中，无论是使用四元数、旋转矩阵（注意不是变换矩阵）还是旋转矢量，我们均得到了一致的结果。

结语

综上，在进行姿态运算时，一定要理清到底是矢量的旋转还是坐标系的旋转，使用的矩阵到底是旋转矩阵还是变换矩阵，否则很容易获得完全相反的结果。