SVM中参数C的理解

有一些数据，可能是线性可分，但在线性可分状况下训练准确率不能达到100%，即无法让训练误差为0，这样的数据被我们称为“存在软间隔的数据”。此时此刻，我们需要让我们决策边界能够忍受一小部分训练误差，我们就不能单纯地寻求最大边际了。

因为对于软间隔地数据来说，边际越大被分错的样本也就会越多，因此我们需要找出一个”最大边际“与”被分错的样本数量“之间的平衡。因此，我们引入松弛系数$\zeta$和松弛系数的系数$C$作为一个惩罚项，来惩罚我们对最大边际的追求。

参数$C$用于权衡”训练样本的正确分类“与”决策函数的边际最大化“两个不可同时完成的目标，希望找出一个平衡点来让模型的效果最佳。

参数	描述
$C$	浮点数，默认1，必须大于0，可不填。松弛系数的惩罚项系数。如果C值设定比较大，那SVC可能会选择边际较小的，能够更好地分类所有训练点的决策边界，不过模型的训练时间也会更长。如果C的设定值较小，那SVC会尽量最大化边界，决策功能会更简单，但代价是训练的准确度。换句话说，C在SVM中的影响就像正则化参数对逻辑回归的影响。

在实际使用中，$C$和核函数的相关参数（$gamma$，$degree$等等）们搭配，往往是SVM调参的重点。与$gamma$不同，$C$没有在对偶函数中出现，并且是明确了调参目标的，所以我们可以明确我们究竟是否需要训练集上的高精确度来调整$C$的方向。默认情况下$C$为1，通常来说这都是一个合理的参数。 如果我们的数据很嘈杂，那我们往往减小$C$。当然，我们也可以使用网格搜索或者学习曲线来调整$C$的值。

那我们的参数$C$如何影响我们的决策边界呢？在硬间隔的时候，我们的决策边界完全由两个支持向量和最小化损失函数（最大化边际）来决定，而我们的支持向量是两个标签类别不一致的点，即分别是正样本和负样本。然而在软间隔情况下我们的边际依然由支持向量决定，但此时此刻的支持向量可能就不再是来自两种标签类别的点了，而是分布在决策边界两边的，同类别的点。

此时我们的虚线超平面$\mathbf{w}\cdot {\mathbf{x}}_{\mathbf{i}}+b=1-\zeta$是由混杂在红色点中间的紫色点来决定的，所以此时此刻，这个紫色点就是我们的支持向量了。**所以软间隔让决定两条虚线超平面的支持向量可能是来自于同一个类别的样本点，而硬间隔的时候两条虚线超平面必须是由来自两个不同类别的支持向量决定的。**而$C$值会决定我们究竟是依赖红色点作为支持向量（只追求最大边界），还是我们要依赖软间隔中，混杂在红色点中的紫色点来作为支持向量（追求最大边界和判断正确的平衡）。如果$C$值设定比较大，那SVC可能会选择边际较小的，能够更好地分类所有训练点的决策边界，不过模型的训练时间也会更长。如果$C$的设定值较小，那SVC会尽量最大化边界，尽量将掉落在决策边界另一方的样本点预测正确，决策功能会更简单，但代价是训练的准确度，因为此时会有更多红色的点被分类错误。换句话说，$C$在SVM中的影响就像正则化参数对逻辑回归的影响。

此时此刻，所有可能影响我们的超平面的样本可能都会被定义为支持向量，所以支持向量就不再是所有压在虚线超平面上的点，而是所有可能影响我们的超平面的位置的那些混杂在彼此的类别中的点了。观察一下我们对不同数据集分类时，支持向量都有哪些？软间隔如何影响了超平面和支持向量，就一目了然了。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs,make_circles,make_moons,make_classification
from sklearn.svm import SVC
%matplotlib inline

#定义决策可视化函数
def plot_svc_decision_function(model,ax=None):
    if ax == None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    
    axisx = np.linspace(xlim[0],xlim[1],30)
    axisy = np.linspace(ylim[0],ylim[1],30)
    
    axisx,axisy = np.meshgrid(axisx,axisy)
    xy = np.vstack([axisx.ravel(),axisy.ravel()]).T
    
    Z = model.decision_function(xy).reshape(axisx.shape)
    
    ax.contour(axisx,axisy,Z
              ,colors = 'k'
              ,levels = [-1,0,1]
              ,linestyles = ['--','-','--']
              )
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

#创建数据
data = make_moons(n_samples = 500,noise = 0.2,random_state=0)
X = data[0]
y = data[1]

#绘制决策过程
plt.figure(figsize = (20,6))
plt.subplot(1,2,1)
clf1 = SVC(kernel='rbf',C=0.5).fit(X,y)
clf2 = SVC(kernel='rbf',C=10).fit(X,y)

plt.scatter(X[:,0],X[:,1],c=y,cmap='rainbow',s=5)
plot_svc_decision_function(clf1)
plt.scatter(clf1.support_vectors_[:,0],clf1.support_vectors_[:,1],facecolor = 'none',edgecolor = 'k')#绘制支持向量

plt.subplot(1,2,2)
plt.scatter(X[:,0],X[:,1],c=y,cmap='rainbow',s=5)
plot_svc_decision_function(clf2)
plt.scatter(clf2.support_vectors_[:,0],clf2.support_vectors_[:,1],facecolor = 'none',edgecolor = 'k')#绘制支持向量

print(clf1.score(X,y))
print(clf2.score(X,y))
print(clf1.support_vectors_.shape)
print(clf2.support_vectors_.shape)

0.956
0.972
(118, 2)
(55, 2)

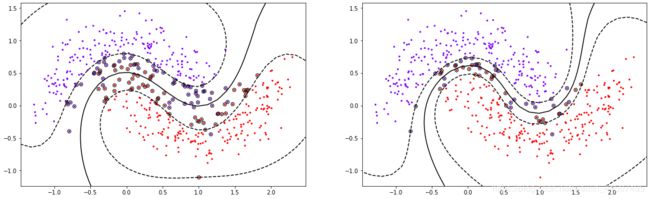
黑色圈圈出的就是我们的支持向量，大家可以看到，所有在两条虚线超平面之间的点，和虚线超平面外，但属于另一个类别的点，都被我们认为是支持向量。并不是因为这些点都在我们的超平面上，而是因为我们的超平面由所有的这些点来决定，我们可以通过调节$C$来移动我们的超平面，让超平面过任何一个白色圈圈出的点。参数$C$就是这样影响了我们的决策，可以说是彻底改变了支持向量机的决策过程。

随着$C$值的增加，决策边界缩小，模型会更加的拟合训练数据，但C值的增加与模型的效果并不是呈线性关系增长的。