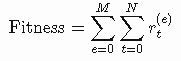剖析强化学习 - 第五部分

作者：Massimiliano Patacchiola

正如我在上一篇中承诺的那样，我将在第五部分介绍进化算法，特别是遗传算法（GA）。如果你阅读完第四篇文章，你应该知道GA可以被认为是Actor-only的算法，这意味着他们直接在策略空间中搜索而不需要效用函数。GAs通常被认为是与强化学习分开的，实际上，GA不关注潜在的马尔可夫决策过程以及Agent在其生命周期中选择的动作。使用这些信息可以实现更高效的搜索，但在某些情况下可能会造成误导。例如，当状态被搞错或部分隐藏时，标准的强化学习算法可能有问题，在同样的场景中，GAs玩起来很安全，但是需要付出代价。当搜索空间很大时，收敛可能会慢得多，因为GA会评估任何类型的策略。在这一系列思想之后，Sutton和Barto并没有将GAs纳入强化学习的圣书中。这篇文章的参考资料是两本书，第一个是Goldberg的“搜索，优化和机器学习中的遗传算法”；第二个是Melanie Mitchell的“遗传算法介绍”。此外，您可能会发现一篇有用的文章“强化学习的进化算法”，在几页中进行了快速的介绍。读者必须意识到，最近的工作突出了进化策略如何成为最先进的强化学习方法的有效替代方案。在Karpathy等人的OpenAI博客最近的一篇文章中，他们指出了这一点，进化方法是高度并行的，当应用于神经网络时，他们不需要反向传播步骤。从这个意义上讲，进化算法可以获得与先进强化学习技术经过相当短的训练后获得的性能相当[论文]。

我将以关于我过去使用GAs经历的短篇故事开始这篇文章。这个故事与强化学习没有直接关系，但可以让你了解GAs可以做什么。毕业后，我迷上了GAs，在此期间，我开始在自主机器人和人工生命实验室工作了一年，在那里我将GAs应用到自动机器人，目标是研究简单交互中出现的复杂行为。采取一组简单的有机体由一个基本的神经网络控制，然后让它们在相同的环境中进化。会发生什么？在大多数情况下，没有什么特别的，最糟糕的是机器人四处游荡，没有目标，而最好的却非常自私。但在某些情况下，可以观察群体行为，机器人开始合作，因为他们注意到它会带来更高的回报，复杂的行为通过简单实体的交互而产生。这就是所谓的涌现(emergence)，它是演化机器人和群体机器人中的一个众所周知的现象。

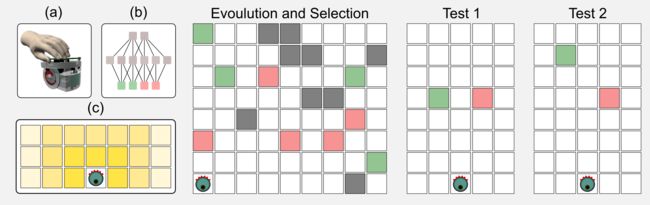
在同一时期，我正在研究单机器人在跨期选择(intertemporal choice)任务中的决策策略。跨期选择涉及到可以在不同时间点获得的选择：今天购买奢侈品或节省资金，以确保未来有可观的养老金。在这些实验中，我使用了由简单神经网络[见图（b）]控制的模拟电子圆盘机器人 [见图（a）]。机器人的传感器可以定位两个令牌的存在：绿色和红色。如图（c）所示，当令牌靠近机器人时，传感器返回更强的信号，传感器信号是网络的输入，而输出是机器人两个轮子的速度。在第一阶段控制机器人的神经网络是在进化策略之后发展起来的，环境中的绿色（高能量）和红色（低能量）令牌的比例被设置，导致丰富或贫乏的生态环境。在称为测试阶段的第二阶段，机器人必须选择单一的绿色或红色标记，令牌与机器人放置在相同的距离，但其中一个在每次新的试验中移动很远。当令牌与机器人距离相同时，它选择高能量令牌，然而，将高能量令牌移动到远处会增加对较低能量的令牌的偏好。机器人策略随着进化过程中使用的生态类型而改变，例如，较差的生态环境增加了对绿色令牌的偏好，这种行为已经在许多动物中观察到，特别是在老鼠中。使用Gas进化的简单神经网络可以代表如此复杂的决策策略，这是令人难以置信的。如果您对这个主题感兴趣，您可以在我与我的同事发表的文章中找到更多内容：“通过实验性进化机器人研究跨期选择”，这是进化算法的实际应用之一。

我将以直观的介绍开始这篇文章，这应该有助于不熟悉进化方法的读者。介绍之后，我将剖析GAs背后的主要概念，并且将介绍一些Python代码。我将介绍许多新术语，因为GAs的惯用语与强化学习中使用的不同。

进化算法（鸟类）

1831年12月27日，HMS比格尔号从英格兰的普利茅斯航行，船上有查尔斯达尔文，自然选择理论之父。这次远征计划只有两年，但持续了五年。比格尔访问了巴西、巴塔哥尼亚、麦哲伦海峡、智利、加拉帕戈斯等地。在旅行期间，达尔文记录了这些地方的生物学、地质学和无脊椎动物学。后来他在一本名为“小猎犬的航行”的书中发表了这些笔记。达尔文在旅行期间发现了什么？

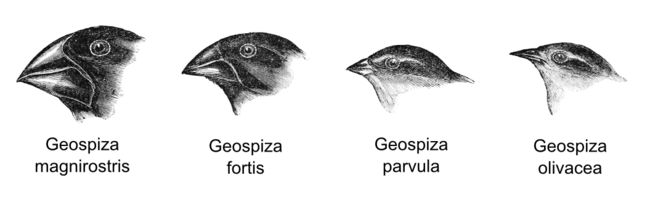
在访问加拉帕戈斯时，达尔文注意到一些鸟类的存在，这些鸟类似乎是从一个祖先的群体进化而来的。这些鸟有共同的特征，但它们的特点是喙形和功能有显著的多样性。达尔文假设，在不同小岛上分离每个物种是导致这种高度分化的原因，特别是喙的形状根据该岛上的食物供应情况而演变。强喙的物种可以吃坚硬的种子，而小喙的物种首选昆虫。

·        Geospiza magnirostris：可以吃坚硬种子的大型鸟类。

·        Geospiza fortis：喜欢小而柔软的种子的中等大小鸟类。

·        Geospiza parvula：喜欢中型昆虫的小型鸟类。

·        Geospiza olivacea：喜欢吃小昆虫的小尺寸鸟类。

达尔文逐渐发现越来越多的证据证明了这一假说，并最终提出了自然选择理论。今天我们称加拉帕戈斯鸟为达尔文的雀科，达尔文的雀科被如此隔离，以至于当环境发生变化时，有可能观察到几代的迅速演变。例如，Geospiza fortis通常喜欢软种子，然而在七十年代，严重的干旱减少了种子的供应，这种雀科被迫转向较硬的种子，导致两代的喙尺寸变化10％。这里发生了什么？物种如何迅速变化？自然选择如何运作？

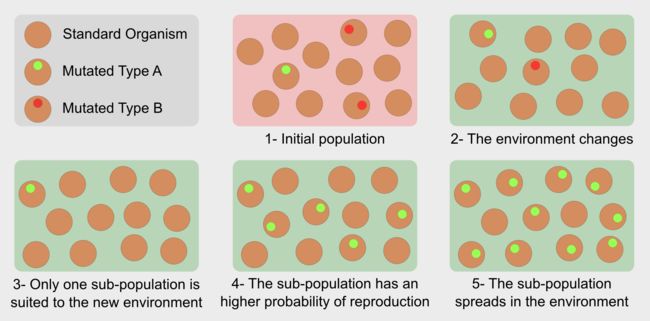
在普通群体中，个体是两个父母之间杂交(crossover)的结果，杂交是父母遗传物质重组的一种形式。在孤立的群体中，遗传物质的冗余会带来非常相似的个体，然而，随机突变可能会改变新生儿的基因型，从而产生具有新特征的生物体。例如，在达尔文的雀科中，它们有一个更强的喙。突变可以为受试者带来优势，从而延长寿命并提高再生率，相反，如果突变没有任何优势，它会在选择过程中被丢弃。就是这样，进化选择最适合特定环境的突变的个体，从这个意义上说，进化不是“最强大的生存者”，而是“最适合的生存者”。

进化算法使用受自然选择（繁殖，突变，重组和选择）启发的算子，他们是优化者，意味着他们直接在解决方案空间中寻找解决问题的方法，候选解决方案是像加拉帕戈斯鸟的单个个体。在标准方法中，使用一系列步骤来评估和选择最佳解决方案：

1.适应度函数(Fitness function)：评估每个候选人的表现

2.选择(Selection)：根据自己的适应性评分选择最佳个体

3.重组(Recombination)：它复制和重组个体

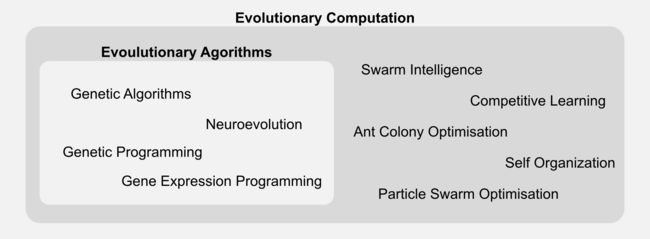
进化算法是更广泛的种类的一部分，称为进化计算。通用分类“进化算法”适用于许多表示和实现细节不同的技术，在这里我只关注遗传算法，但是你应该知道它有很多变种。

在下一节中，我将介绍遗传算法(GAs),它被认为是一种特殊类型的进化算法。我将描述所有新术语，并将其与过去episode中遇到的术语相比较。

遗传算法

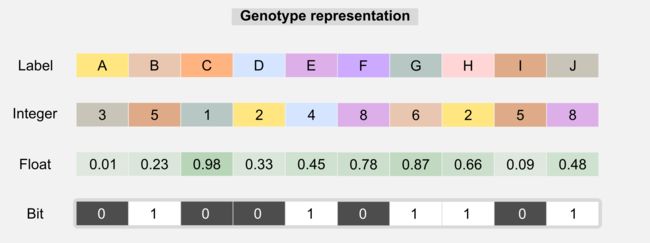
上一节我们了解了进化算法的工作原理，在本节中，我将深入解释GAs是如何工作的。顾名思义，遗传算法涉及基因，选择的隐喻继续在这里起作用，但它适用于遗传物质。这个想法是用特定的基因型（或染色体）来描述群体中的每一个体，这是用来表达个体的特征或表型(phenotype)。在生物学中，基因型代表生物体的遗传信息，表型是该生物体的观察特征和行为。基因型和表型之间的区别和他们的交互很容易被误解，基因型只是影响表型的因素之一，非遗传因子和获得性突变不是基因型的一部分，但对表型有影响。在GAs中，基因型通常由一维数组表示，其中每个值（有时称为基因）代表一个属性。

基因型可以包含标签、浮点数、整数或位，为了使用遗传算子，染色体中的类型保持一致通常是必需的。基于标签的基因型可用于破解编码，GAs可以在大型解决方案空间中进行搜索，以便正确进行解密；基于整数的基因型用于网络拓扑优化；基于浮点的基因型可以包含神经网络的权重，并且可以使用GAs而不是反向传播来调整这些权重，这种优化是我用来发展电子盘机器人的一种优化（参见介绍），选择正确的染色体表示通常取决于设计者。设计师的另一项任务是适应度函数，适应度函数是任何遗传算法的核心，找到正确的答案至关重要。适应度函数为问题提供了答案：给定解决方案离实现目标有多接近？在许多应用中，我们可以使用多种适应度函数。例如，如果我们正在发展无人机的控制器，那么可以通过无人机在空中停留多久来定义适应度函数，但是，此功能不包含有关飞行稳定性的任何信息，更好的可以考虑用惯性单元返回的值给稳定性更高的控制器带来更高的分数。选择正确的适应度函数可能需要使用GAs的某些经验，但对于许多问题，近似适应度也可能导致良好的解决方案。在下一节中，我将向你展示适应度函数如何与强化学习中的奖励概念相关联。下面描述GAs中可用的所有算子以及它们如何用于进化过程。

选择(Selection)：选择是一种减少可能的解决方案数量的方法，选择导致最佳结果的解决方案。适应度评估后，可以将染色体从最佳状态到最差状态进行排序，选择机制使用有序列表。有不同类型的选择，截断选择(Truncated selection)是最简单的选择形式，仅选择染色体总数的一小部分，其余部分被拒绝。

更复杂的选择形式称为轮盘(roulette wheel)。给每个染色体赋予一个权重，这个权重对应于轮盘的一部分，具有较高适应度的染色体将具有较高的权重和较大的轮子部分。在不同的时间旋转轮子可以为下一代选择个体。轮盘不过是一种加权分类机制，你必须注意到，使用轮盘可以将相同的染色体多次排序，并且它在下一代中出现的概率更高。另一种形式的选择称为锦标赛选择(tournament selection)，它包括随机选择一组个人，并仅选取适合度最高的选手。

选择过程可以将一些个体标记为精英(elite)，这意味着他们的基因型将没有变化地被复制到新一代，这种机制被称为精英主义(elitism)，用于保持进化循环中的最佳解决方案。我将在python实现中使用elitism，例子会在功能上给你展示更多的内容。

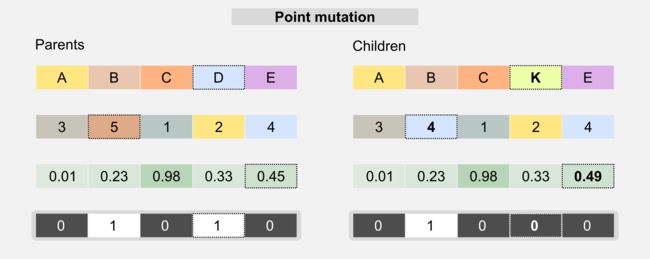
突变(Mutation)：使用该算子是为了避免群体中的一致性。突变随机改变基因型的一个值，随机更改现有解决方案，以避免搜索空间中的局部最小值。最简单的突变称为点突变(point mutation)，与DNA上的生物机制相似。

突变概率通常由必须仔细选择的突变率来描述。高突变率可导致最佳个体的丧失，而低突变率会导致基因型的一致性。对于基于标签和基于整数的染色体，突变会将单个基因更改为从预定义集合中随机选取的值；对于基于位的染色体，当突变发生时，基因的值切换到与其相反的位置；在基于浮点的染色体中，值可以从均匀分布或从以基因值为中心的高斯分布中采样。

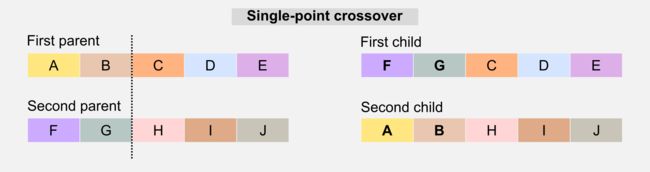
杂交(Crossover)：该算子类似于生物学的对应物，它用于重组父母的基因型以产生具有混合特征的后代。最简单的杂交形式称为单点(single-point)，鉴于两个父母的基因型和一个随机切片点，当生成孩子时，单点杂交直接“交叉”这两个部分。

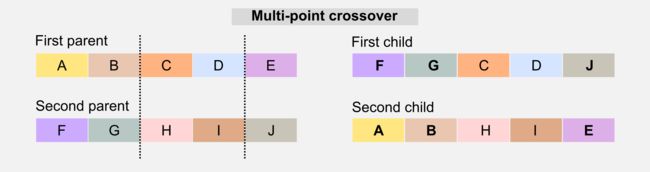
另一个版本的杂交称为多点杂交(multi-pointcrossover)。多点杂交选择多个切点并重新组合孩子基因型中的那些部分。

还有其他的交叉解决方案涉及多个父母，但在接下来的部分中，我将只关注单点版本。

强化学习中的GAs

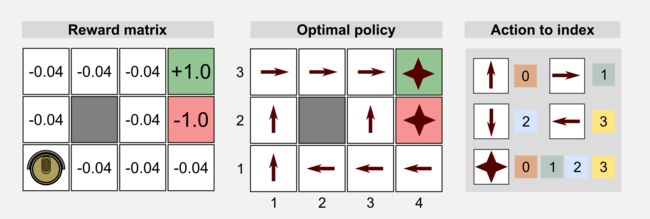
我们如何在强化学习中使用GAs？GAs可用于策略评估，在这种情况下，一维基因型是策略矩阵的表示。在下面的章节中，我将交替使用基因型和染色体。像往常一样，我将从第一篇文章中介绍的清洁机器人示例开始。清洁机器人可以在4x3离散世界中移动，每个状态的奖励是-0.004，不同的奖励是充电站（+1.0）和楼梯（-1.0）。环境不确定，机器人采取的每个动作都有20％的失败概率，目的是给出这种环境的最佳策略。这里我们想看看GAs是否可以通过重组群体染色体来获得最优策略。我们可以使用基于整数的表示法，每个数字对应一个动作：0 = UP，1 =右，2 =下，3 =左。对于终止状态和障碍，我们并不需要采取动作，因为在这些状态下动作不会发生。出于这个原因，我们可以使用随机值来表示动作，或者我们可以从染色体中丢弃这些状态。为了清楚起见，我选择了第一种解决方案。

我们可以将基因型表示为将动作与每个状态相关联的展开的策略矩阵。从状态（1,1）（列x行）开始，遵循网格世界的Russel和Norvig约定（起点位于左下角），我们将每个动作与一个索引关联，并将每个值存储在染色体中。

起始群体将具有随机初始基因型，这意味着每个机器人的行为将会不同。适应度分数可以使我们区分好和坏的策略，这里适应度值被定义为所有的M episode中在每个时间步t获得的奖励总和：

在多个episode中对染色体进行评估以更好地评价其表现。这里探索开始的条件是必要的，以保证对搜索空间的广泛探索。我们可以总结两点：

·        基因型（或染色体）表示策略矩阵

·        适应度分数表示在多个episode中的累积奖励

了解基因算子如何修改染色体/策略是很有趣的。突变随机修改在特定状态下所采取的动作，该算子保证了解决方案空间的探索；杂交使用两个染色体进行混合。假设我们有两个父母，第一个是在网格世界的上半部分特别好的策略，但在下半部分则不太好，第二个父母代表了一个在下半部分是好的策略，但在上半部分却是非常糟糕的，通过单点杂交混合这两条染色体会产生两个孩子，一个非常好，另一个非常糟糕。现在是时候用Python实现一切了。

Python实现

Python实现建立在代表上述遗传算子的不同功能上。首先，我们需要一个函数来生成随机的染色体群体，使用Numpy方法numpy.random.choice()可以在一行中完成，染色体的每个值都是从预定义集合中选取的基因。在我们的案例中，该集合由机器人可以选择的四个离散动作表示[0, 1, 2,3]。

 

def return_random_population(population_size, chromosome_size, gene_set):
    '''Returns a random initialised population

    This funtion initialise a matrix of integers using numpy randint.
    @param chromosome_size 
    @param population_size
    @param gene_set list or array containing the gene values
    @return matrix of integers size:
         population_size x chromosome_size
    '''
    return np.random.choice(gene_set, 
                            size=(population_size,chromosome_size))

一旦随机群体准备就绪，我们就可以估计每个个体的适应度从而获得一个适应度数组。我们需要一个函数来按好-差顺序对染色体进行排序，在Numpy中，方法numpy.argsort()返回数组中值从最低到最高（差-好）的位置，此方法特别有效，因为默认情况下它使用快速排序算法。在最后一步中，我们必须颠倒这些元素的顺序来获得我们正在寻找的好-差的列表。一切都可以用Python在几行中实现：

 

def return_best_worst_population(population, fitness_array):
    '''Returns the population sorted in best-worst order

    @param population numpy matrix containing the population chromosomes
    @param fitness_array numpy array containing the fitness score for
        each chromosomes
    @return the new population and the new fitness array
    '''
    new_population = np.zeros(population.shape)
    new_fitness_array = np.zeros(fitness_array.shape)
    worst_best_indeces = np.argsort(fitness_array)
    best_worst_indeces = worst_best_indeces[::-1] #reverse the array
    row_counter = 0
    for index in best_worst_indeces:
         new_population[row_counter,:] = population[index,:]
         new_fitness_array[row_counter] = fitness_array[index]
         row_counter += 1
    return new_population, new_fitness_array

一旦我们有了排序的群体，就有可能选择最好的个体。所述截断选择机制可以使用numpy的方法numpy.resize()来实现，该方法需要输入一个矩阵，并返回它的一部分。

 

def return_truncated_population(population, fitness_array, new_size):
     '''Truncates the input population and returns part of the matrix

     @param population numpy array containing the chromosomes
     @param fitness_array numpy array containing the fitness score for
         each chromosomes
     @param new_size the size of the new population
     @return a population containing new_size chromosomes 
     '''
     chromosome_size = population.shape[1]
     pop_size = population.shape[0]
     new_population = np.resize(population, (new_size,chromosome_size))
     new_fitness_array = np.resize(fitness_array, new_size)
     return new_population, new_fitness_array

在之前的部分中，我展示了另一种选择机制，即轮盘。使用Numpy方法numpy.random.choice()可以很容易地实现轮盘，该方法可以将表示与输入数组的每个元素相关的概率的数组作为输入。因为概率必须总和为1，所以我们必须使用softmax函数来对包含在适应度数组中的值进行归一化。

 

def return_roulette_selected_population(population, fitness_array, new_size):
  '''Returns a new population of individuals (roulette wheel).

  Implementation of a roulette wheel mechanism. The population returned
  is obtained through a weighted sampling based on the fitness array.
  @param population numpy matrix containing the population chromosomes
  @param fitness_array numpy array containing the fitness score for
      each chromosomes
  @param new_size the size of the new population
  @return a new population of roulette selected chromosomes, and
          the fitness array reorganised based on the new population.
  '''
  #Softmax to obtain a probability distribution from the fitness array.
  fitness_distribution = np.exp(fitness_array - 
                         np.max(fitness_array))/np.sum(np.exp(fitness_array - 
                                                       np.max(fitness_array)))
  #Selecting the new population indeces through a weighted sampling
  pop_size = population.shape[0]
  chromosome_size = population.shape[1]
  pop_indeces = np.random.choice(pop_size, new_size, p=fitness_distribution)
  #New population initialisation
  new_population = np.zeros((new_size, chromosome_size))
  new_fitness_array = np.zeros(new_size)
  #Assign the chromosomes in population to new_population
  row_counter = 0
  for i in pop_indeces:
      new_population[row_counter,:] = np.copy(population[i,:]) 
      new_fitness_array[row_counter] = np.copy(fitness_array[i])
      row_counter += 1
  return new_population, new_fitness_array

GA的下一步是杂交功能。有不同的方式来实现杂交，在这里，父母从输入群体中随机抽样，并创建一个new_size大小染色体的新个体。在这个简化版本中，两个父母只生成一个孩子，切片点是随机定义的，孩子染色体的第一部分含有第一个亲本基因，而第二部分则来自第二个亲本。elite参数定义了多少个体在未被杂交的情况下被复制到新的群体中，在使用精英主义时，群体必须从最好到最差排序。

 

def return_crossed_population(population, new_size, elite=0):
    '''Return a new population based on the crossover of the individuals

    The parents are randomly chosen. Each pair of parents generates
    only one child. The slicing point is randomly chosen.
    @param population numpy matrix containing the population chromosomes
    @param new_size defines the size of the new population
    @param elite defines how many chromosomes remain unchanged
    @return a new population of crossed individuals
    '''
    pop_size = population.shape[0]
    chromosome_size = population.shape[1] 
    if(elite > new_size): 
        ValueError("Error: the elite value cannot " +
                    "be larger than the population size")
    new_population = np.zeros((new_size,chromosome_size))
    #Copy the elite into the new population matrix
    new_population[0:elite] = population[0:elite]
    #Randomly pick the parents to cross
    parents_index = np.random.randint(low=0, 
                                      high=pop_size, 
                                      size=(new_size-elite,2))
    #Generating the remaining individuals through crossover
    for i in range(elite,new_size-elite):
        first_parent = population[parents_index[i,0], :]
        second_parent = population[parents_index[i,1], :]
        slicing_point = np.random.randint(low=0, high=chromosome_size)
        child = np.zeros(chromosome_size)
        child[0:slicing_point] = first_parent[0:slicing_point]
        child[slicing_point:] = second_parent[slicing_point:]
        new_population[i] = np.copy(child)
    return new_population

最后是突变算子。突变遍历所有染色体的所有值，并且对于每个值从预定义集合中挑选整数的内容进行随机突变。在我们的案例中，该集合表示机器人可用的四个动作[0, 1, 2,3]。我们可以使用函数numpy.nditer()来更改Numpy数组，只要从均匀分布中提取的随机浮点数小于mutation_rate。elite参数表示群体矩阵中个体的数量保持不变。正如我在前一节中解释的那样，精英主义对于保存有史以来最好的解决方案非常有用。

 

def return_mutated_population(population, gene_set, mutation_rate, elite=0):
    '''Returns a mutated population

    It applies the point-mutation mechanism to each value
    contained in the chromosomes.
    @param population numpy array containing the chromosomes
    @param gene_set a numpy array with the value to pick
    @parma mutation_rate a float repesenting the probaiblity 
        of mutation for each gene (e.g. 0.02=2%)
    @return the mutated population
    '''
    for x in np.nditer(population[elite:,:], op_flags=['readwrite']):
        if(np.random.uniform(0,1) < mutation_rate):
            x[...] = np.random.choice(gene_set, 1)
    return population

现在我们必须把所有东西都放到一起看看我们得到了什么。首先要做的是定义一些需要调整的超参数，可以通过修改这些参数中的每一个来获得不同的结果。增加tot_episodes你会得到一个更好的适应度估计；tot_steps定义了每个episode允许多少个步骤，对于网格世界来说，行数加上列数的2倍是一个比较好的值；population_size应随着相应的状态空间增加而增加，更大的空间可能需要更多的群体；elite_size大体对应于总群体的10％，这个参数不应该太高，否则总体会过于统一；mutation_rate真的很重要，这里我使用了10％的值，但通常使用5％的概率。我推荐你用不同的参数运行脚本，看看会发生什么。gene_set和chromosome_size是特定于4x3的网格世界的参数，如果要在其他应用程序中重新使用代码，则应该修改它们。

 

tot_generations = 100
tot_episodes = 100
tot_steps = 14
population_size = 100
elite_size = 10
mutation_rate = 0.10
gene_set = [0, 1, 2, 3]
chromosome_size = 12

定义超参数后，我们必须生成初始群体，对于4x3的网格世界来说，在return_random_population()函数中有足够的100个染色体可以随机初始化。之后是设置主循环的时间，用探索开始条件评估每个染色体100个episode，所有episode中的适应度都会累积。适应度评估后，第一步就是选择，这里的轮盘选择被注释，因为我将使用一个简单的只占群体的一半的截断选择。

 

for generation in range(tot_generations):
  #The fitness value for each individual is stored in np.array
  fitness_array = np.zeros((population_size))
  for chromosome_index in range(population_size):
    for episode in range(100):
      #Reset and return the first observation
      observation = env.reset(exploring_starts=True)
      for step in range(30):
        #Estimating the action for that state
        col = observation[1] + (observation[0]*world_columns)
        action = population_matrix[chromosome_index,:][col]
        #Taking the action and observing the new state and reward
        observation, reward, done = env.step(action)
        #Accumulating the fitness for this individual
        fitness_array[chromosome_index] += reward
        if done: break

  #Uncomment the following lines to enable roulette wheel selection
  #population_matrix, fitness_array = \
    #return_roulette_selected_population(population_matrix,
                                        #fitness_array,
                                        #population_size)
  population_matrix, fitness_array = \
    return_best_worst_population(population_matrix, fitness_array)
  #Comment the following line if you enable the roulette wheel
  population_matrix, fitness_array = \
    return_truncated_population(population_matrix, 
                                fitness_array, 
                                new_size=int(population_size/2))
  population_matrix = return_crossed_population(population_matrix, 
                                                population_size, 
                                                elite=10)
  population_matrix = return_mutated_population(population_matrix,
                                                gene_set=[0,1,2,3],
                                                mutation_rate=mutation_rate, 
                                                elite=10)

像往常一样，完整的代码在我的GitHub仓库中，名称是genetic_algorithm_policy_estimation.py。我设定mutation_rate=0.10和elite_size=10，加载脚本将给出平均适应度分数，以及每代的最佳和最差的个体评分。

 

Generation: 1
Fitness Mean: -94.4964
Fitness STD: 35.5458518964
Fitness Max: 18.24 at index 57
Fitness Min: -142.2 at index 79

Generation: 2
Fitness Mean: -63.348
Fitness STD: 32.8610677855
Fitness Max: 20.64 at index 71
Fitness Min: -116.6 at index 46

Generation: 3
Fitness Mean: -46.9696
Fitness STD: 35.4612189841
Fitness Max: 41.36 at index 60
Fitness Min: -127.32 at index 37

...

Generation: 10
Fitness Mean: 17.7552
Fitness STD: 56.6485542354
Fitness Max: 75.4 at index 1
Fitness Min: -131.72 at index 72

...

Generation: 50
Fitness Mean: 35.9964
Fitness STD: 54.7041918964
Fitness Max: 83.84 at index 26
Fitness Min: -122.64 at index 21

...

Generation: 100
Fitness Mean: 39.4068
Fitness STD: 53.0702770462
Fitness Max: 82.36 at index 55
Fitness Min: -126.0 at index 22

我们应该如何解读这些信息？当选择机制工作时，平均适应度增加。在我们的例子中，我们可以看到它从第1代的-94.5到第3代的-47.0，最终在100代中达到了39.4分。最好的和最差的个体的得分可能会不稳定，因为这些个体是离群点，他们的表现可能有很大的差异。对于最好的和最差的个体，你可以在适应度数组中看到相应的指标。该指标对于理解最佳个体是否是精英的一部分（在我们的例子中是前10个对象）是有用的，当个体不属于精英时，这意味着遗传算子设法在精英之外寻找更好的解决方案。例如，在第10代中，第一个人获得了最高的适应度，而在第50代中，则是第26的个体。在第一种情况下，最好的是精英的一部分，而第二种情况则不是。

标准偏差是一个重要信息，因为它可以告诉我们在群体中是否有遗传冗余。当标准差偏低时，这意味着个体具有相似的表现，这可能是由于染色体的均一性。在进化过程中，您可能会看到标准差增加，这表明由于个体基因型中分支的倍增，差异正在变大。

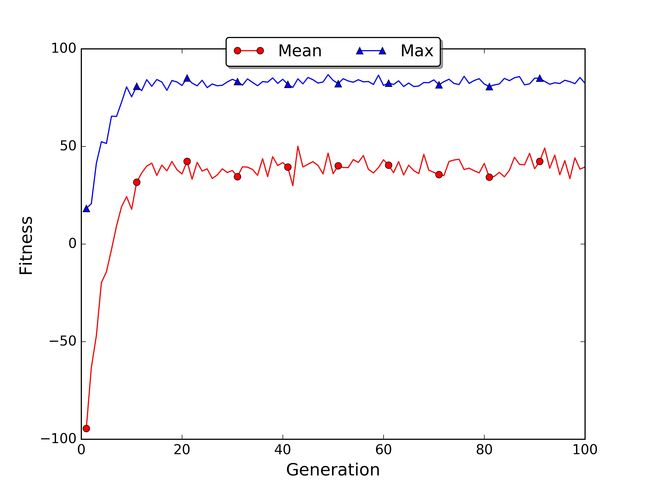
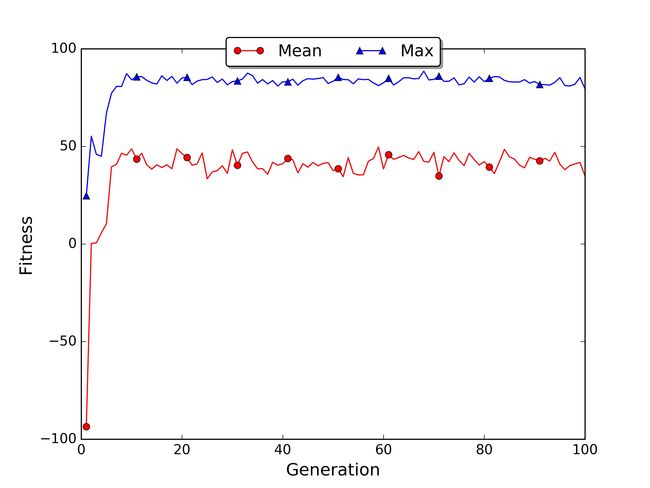
如果你安装了matplotlib，脚本将自动保存文件中每一代的最佳和平均适应度图fitness.jpg。在我的情况下，前20代的平均适应度上升，然后达到高原平台。取消轮盘的代码注释并注释截断选择的代码，我们可以得到轮盘选择的图。

在轮盘的图中，平均适应度增长更快，因为采样机制向下一代移动了更多数量的好的策略。

看看精英（前10个人）他们采用了哪种策略很有意思。在我第100代的模拟中，大多数精英的染色体都是最优或次优的。

 

Optimal Policy:
 >  >  >  *  ^  #  ^  *  ^  <  <  <

Chromosome 1:
 >  >  >  *  ^  #  ^  *  ^  >  ^  < 
Chromosome 2:
 >  >  >  *  ^  #  ^  *  ^  <  <  < 
Chromosome 3:
 >  >  >  *  ^  #  ^  *  ^  <  ^  < 
Chromosome 4:
 >  >  >  *  ^  #  ^  *  ^  >  ^  < 
Chromosome 5:
 >  >  >  *  ^  #  ^  *  ^  <  <  < 
Chromosome 6:
 >  >  >  *  ^  #  ^  *  ^  ^  ^  < 
Chromosome 7:
 >  >  >  *  ^  #  ^  *  ^  v  ^  < 
Chromosome 8:
 >  >  >  *  ^  #  ^  *  ^  >  ^  < 
Chromosome 9:
 >  >  >  *  ^  #  ^  *  ^  <  ^  < 
Chromosome 10:
 >  >  >  *  ^  #  ^  *  ^  <  <  <

如果我们把例子的网格大小放大到30x10，一切都会变得更加困难。在GitHub存储库中，您会发现另一个文件，称为genetic_algorithm_policy_estimation_large_world.py，网格世界的维度为30x10。您可以通过改变环境初始化参数chromosome_size和tot_steps，将脚本重新调整到一个不同的世界，保持population_size和tot_episodes等于100，运行脚本到300代。

 

Generation: 1
Fitness Mean: -313.6372
Fitness STD: 6.56887997759
Fitness Max: -289.44 at index 3
Fitness Min: -320.32 at index 38

Generation: 2
Fitness Mean: -307.286
Fitness STD: 11.1612836179
Fitness Max: -265.88 at index 99
Fitness Min: -321.2 at index 56

Generation: 3
Fitness Mean: -301.32
Fitness STD: 13.0532141636
Fitness Max: -265.24 at index 2
Fitness Min: -320.0 at index 12

...

Generation: 100
Fitness Mean: -236.0288
Fitness STD: 42.1012775407
Fitness Max: -143.88 at index 4
Fitness Min: -320.0 at index 70

...

Generation: 300
Fitness Mean: -220.7844
Fitness STD: 52.0733055283
Fitness Max: -111.16 at index 31
Fitness Min: -320.0 at index 43

训练花了近2个小时，而之前的小世界只有几分钟，在世代生成过程中平均和最大适应度缓慢增加。使用图可视化总趋势，显示有改进的空间。如果你运行脚本产生更多的世代，可以看看适应度何时达到高原平台位置。

正如你在大世界的例子中注意到的那样，遗传方法的局限在于它可能需要许多代才能收敛。此外，它不能像我们在时间差分学习中看到的那样在线学习。由于这些原因，GA通常用于模拟环境中，其中世界的多个实例可以并行运行并且计算上并不昂贵。

结论

在这篇文章中，我介绍了进化和遗传算法。GA基于自然选择机制，可用于直接在策略空间中搜索策略。在强化学习中，当马尔可夫决策过程的状态被部分隐藏或错误时，使用GA可能是有利的。我在这篇文章中发布的python代码是通用的，可以应用于各种各样的问题，您可随意将其用于您自己的应用程序。此外，您可以在网上找到基于可在浏览器上运行的GAs的模拟器，在资源部分有几个示例的链接。

这篇文章可以被看作是本系列第一部分的结论，我们准备将迄今积累的知识应用于更复杂的问题。强化学习是一个很好的工具，它可以应用在很多场景下，下一篇文章我会告诉你它的更大的潜力。

 

索引

1. [第一篇]马尔科夫决策过程，贝尔曼方程，值迭代和策略迭代算法。

2.  [第二篇]蒙特卡罗概念，蒙特卡洛方法，预测与控制，广义策略迭代，Q函数。

3.  [第三篇]时间差分概念，动物学习，TD(0), TD(λ)和资格痕迹，SARSA，Q-learning。

4.  [第四篇]Actor-Critic方法背后的神经生物学，计算Actor-Critic方法，Actor-only和Critic-only方法。

5.  [第五篇]进化算法介绍，强化学习中的遗传算法，遗传算法的策略选择。

6.  [第六篇]强化学习应用，多臂老虎机，山地车，倒立摆，无人机着陆，难题。

7.  [第七篇]函数逼近概念，线性逼近器，应用，高阶逼近器。

8. [第八篇] 非线性函数逼近，感知器，多层感知器，应用，政策梯度。

资源

·   The complete code for the GeneticAlgorithm examples is available on the dissecting-reinforcement-learning officialrepository on GitHub.

·        Scholarpedia article on Neuroevolution [web]

·        Genetic algorithm walkers simulator [web]

·        Genetic algorithm cars simulator [web]

·        List of genetic algorithm applications [wiki]

·        Evolutionary Algorithmsfor Reinforcement Learning. Moriarty, D. E., Schultz, A. C., &Grefenstette, J. J. (1999). [pdf]

·        Reinforcement learning:An introduction (Chapter 1.3) Sutton, R. S., & Barto, A. G. (1998).Cambridge: MIT press. [html]

·        Evolution Strategies asa Scalable Alternative to Reinforcement Learning Salimans,T., Ho, J., Chen, X., & Sutskever, I. (2017). arXiv preprintarXiv:1703.03864. [pdf]

参考

Goldberg,D. E., & Holland, J. H. (1988). Genetic algorithms and machine learning.Machine learning, 3(2), 95-99.

Mitchell,M. (1998). An introduction to genetic algorithms. MIT press.

Moriarty,D. E., Schultz, A. C., & Grefenstette, J. J. (1999). Evolutionary algorithmsfor reinforcement learning. J. Artif. Intell. Res.(JAIR), 11, 241-276.

Paglieri,F., Parisi, D., Patacchiola, M., & Petrosino, G. (2015). Investigatingintertemporal choice through experimental evolutionary robotics. Behaviouralprocesses, 115, 1-18.

Salimans,T., Ho, J., Chen, X., & Sutskever, I. (2017). Evolution Strategies as aScalable Alternative to Reinforcement Learning. arXiv preprintarXiv:1703.03864.